四边简支正交各向异性混凝土空心板的一种计算方法

杨小兵

（太原理工大学建筑设计研究院，山西 太原 030024）

在多层和高层钢筋混凝土建筑中，现浇钢筋混凝土空心楼盖体系应用很广，发展很迅速。高强度薄壁管在现浇砼空心无梁楼盖中的应用，促进了建筑业技术创新，该项技术在降低工程造价、缩短工期、改善隔音效果、提高净空高度、降低建筑自重等方面效益显著，随着技术不断成熟、生产工艺不断完善，必将在建筑业上得到广泛推广应用。

目前，计算正交各向异性板混凝土圆孔空心板的方法很多，但显复杂。因此，本文通过将经典的Navier 双重Fourier三角级数法解法和Rayleigh-Ritz 解法有机地结合起来，求解了均布荷载下四边简支正交各向异性混凝土空心板的内力和挠度。有限元分析表明，该方法概念清晰，计算精度高，完全适合于工程设计。

1 四边简支正交各向同性实心薄板的Navier 解法

小挠度薄板的弹性曲面微分方程

图1 圆孔空心板

图2 四边简支空心板

对于四边简支的矩形薄板，其边界条件为：

在竖向荷载q 作用下，Navier 将w 展开为双重Fourier三角级数：其中：m和n为正整数，Amn为待定系数，显然这种形式的w的表达式满足式（2） 的所有边界条件。联立式（1） 和式（3） 得

在竖向荷载q作用下，可将q和Cmn展开为双重Fourier三角级数：

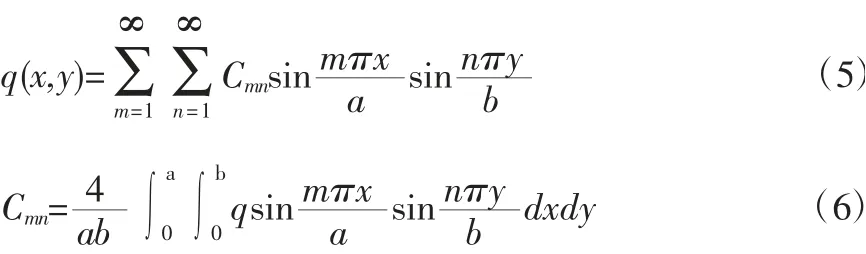
再将式（5） 和式（6） 代入式（4） 可得

其中：m，n 为奇数。

将Amn代入式（3），即可得到w的表达式，再将w的表达式代入式（7），即可求得内力。

当四边简支板在竖向均布荷载q0作用下，任意点（x，y） 处的挠度和内力的表达式为

应用上述公式，可以计算出四边简支正交各向同性实心板中任意点的挠度和内力。但是用来求解弯矩和剪力时，收敛较慢，需要取二三十项。

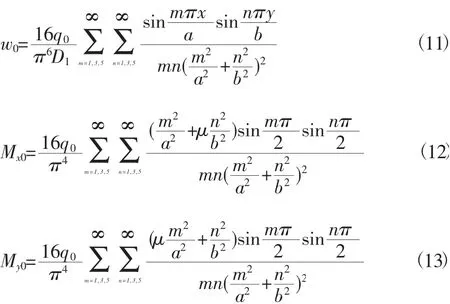
2 正交各向异性圆孔空心板

圆孔板的正交各向异性表现在两个方向的宏观泊松比的不同，即：可以将圆孔空心板作为正交各向异性实心板计算，只是宏观弹性模量要做如下调整：

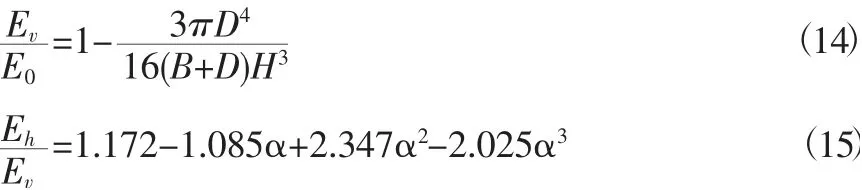
根据弹性力学可知圆孔空心板在垂直于圆孔方向，即横向处于平面受力状态，宏观泊松比不会发生变化，和原来未开孔的实心板是相同的，即μv=μ0

通过基于变分原理的Rayleigh-Ritz 法的推导，可以得出正交各向异性混凝土空心板的内力和挠度与各向同性实心板比值为：

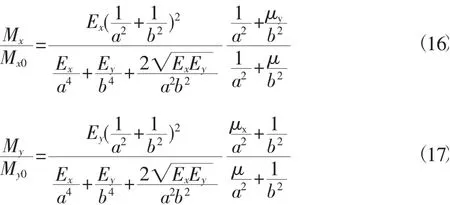
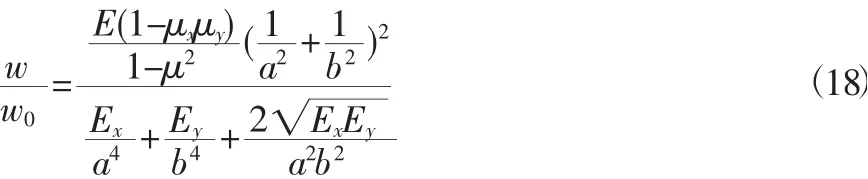
其中：w、Mx、My 为各向异性圆孔空心板的跨中挠度和内力。

3 算例

一混凝土圆孔空心板，混凝土弹性模量E0=3.25×104MPa，泊松比μ0=μv=0.2，跨度为a=b=12m，板厚H 为300mm，承受竖向均布荷载q=10.0kN/m2，孔洞直径D=200mm，孔洞间距

根据式（14） 和式（15） 得出，Ev=2.81×104MPa，Eh=2.51×104MPa，μh=0.179。

根据式（11） 和式（12） 和式（13） 得出，w0=11.06mm，Mx0=63673.85N-m/m，My0=63673.85N-m/m。

Mx=1.0387Mx0=1.0387×63673.85=66138N-m/m比有限元计算值65991 大0.2%；

My=0.9444My0=0.9444×63673.85=60133N-m/m比有限元计算值59673 大0.8%；

w=1.2281wx0=1.2281×11.06=13.58mm比有限元计算值13.57mm 大0.07%

由此可见跨中的内力、挠度误差均很小，采用二重Fourier 三角级数和Rayleigh-Ritz 法求解正交各向异性四边简支板的方法具有相当高的精度，满足工程设计的要求。

4 结语

本文采用二重Fourier 三角级数和Rayleigh-Ritz 法推导的计算公式，可以方便地计算出正交各向异性混凝土圆孔空心板的内力和挠度，进而可以根据混凝土理论进行板的抗裂、承载能力和挠度的计算。该方法概念清晰、计算方便，精度高，可以满足工程设计的要求，值得我们大力推广。

二重Fourier 三角级数形式的解具有很高的理论价值，方法简单方便。虽然挠度、力矩和剪力的级数都是收敛的，但是收敛比较缓慢，应用重三角级数求解挠度需取十多项，求内力需取二三十项。借助office 2003 中Excel 进行计算，可以大大的减少计算量。