碰撞角对船舶碰撞下桥梁动力响应的影响分析
2019-07-19刘静文
刘静文
(西南交通大学,四川成都 610031)
随着我国交通事业的迅猛发展,对斜拉桥等大型桥梁的跨度要求越来越高,船舶的吨位和数量也是与日俱增,船桥碰撞事故也时有发生。船桥碰撞事故的发生,轻则导致桥梁结构损坏,影响桥梁结构使用寿命、降低桥梁安全性;重则导致桥毁人亡,造成重大安全事故。因此,对船舶撞击作用下桥梁结构的受力状况及动力响应的研究有着重要意义[1-3]。
本文以武汉天兴洲长江大桥为工程背景,利用ANSYS建立详细的全桥整体三维有限元模型。将船撞荷载施加到桥梁指定关键点。分析8 000t船舶在不同角度撞击作用下桥梁各关键部位的动力响应,为大跨度公铁两用斜拉桥的防撞设计和安全评估提供参考。
1 工程概况
武汉天兴洲长江大桥是一座双塔三索面三主桁公铁两用斜拉桥,正桥全长4 657m,桥梁跨径(98+196+504+196+98)m。大桥上层公路为六车道,宽27m。下层铁路为四线,其中两线一级干线、两线客运专线。
主梁为板桁结合钢桁架,“N”形桁架,三片主桁,分别锚固于三个索面,三片主桁间距15m,宽30m,高15.2m,节间长度14m。主主桁部分斜杆采用箱型截面,其余斜杆、竖杆采用H形截面。斜拉索锚固于主桁上弦节点,材料为Φ7镀锌钢丝,Ry1=1670MPa。钢梁采用Q370q-E钢。主塔为倒Y形,两侧各有3×16根斜拉索,主塔材料为C50级混凝土。总体布置图如图1所示。

图1 武汉天兴洲长江大桥总体布置(单位:m)
2 有限元模型的建立
2.1 斜拉桥模型
主梁上弦中部756m范围是钢正交异性板桥面,两端各168m范围是混凝土结合板桥面。铁路桥面系采用纵横梁体系,道砟桥面。纵梁与横梁均为“工”字形截面,端横梁采用箱形截面,间隔6个节间设置有制动撑架。公路桥面中部756m范围内,桥面板厚14mm,每半幅桥(15m宽)设四道纵梁,沿纵桥向每14m长节间内设5道横肋。主梁两端各168m范围内,每半幅桥设四道纵梁与正交异性板的纵梁对齐,每个节点处设置公路横梁。
在建模过程中,考虑到运算量,对公路主梁采用了等效格子梁法来模拟正交异性板。将纵肋与横肋用与其中心线重合的梁单元进行模拟,每节间(14m)视作一个梁格。这样,公路桥面即简化为由上弦杆、公路纵梁、公路横梁和横隔板组成的梁格体系[2]。公路纵肋与铁路纵肋的质量与刚度均等效分配到相应纵梁上。然后,采用空间有限元法进行离散。铁路桥面按照实际构造进行建模。主塔主桁、公路横梁纵梁、铁路横梁纵梁铁路桥面板均采用BEAM4单元进行模拟,公路混凝土桥面梁格与钢正交异性板梁格采用SHEEL63单元进行模拟。集中质量运用MASS21单元进行模拟。斜拉索离散成空间杆单元,运用LINK10单元进行模拟。由垂度效应引起的斜拉索几何非线性问题,采用Ernst公式进行弹性模量修正。主梁与拉索之间通过刚度极大的刚臂进行连接,并用实常数定义来实现斜拉索的截面特性。全桥节点共计15 208个,单元共有24 122个。其中桥塔单元776个,主塔刚臂单元434个,斜拉索236个,主梁22 646个,全桥结构计算模型见图2。

图2 武汉天兴洲长江大桥有限元模型
2.2 桥梁模型验证
通过静力分析和模态分析对桥梁模型进行了验证[4-5]。静力分析法通过对模型施加自重荷载,提取了主梁边跨跨中1 139号节点、跨中1 040号节点、主跨3/4跨116号节点的竖向位移进行定性分析。三个节点位移分别为-0.220m、-0.258m和-0.013m,符合实际经验。为进行桥梁自振特性分析,设置了前20阶模态分析,得到前20阶自振频率及相应振型。前10阶自振频率及振型见表1,部分振型图见图3。

(b)2阶(主梁对称竖弯)

(a)1阶(主梁纵振)

(c)3阶(主梁对称侧弯)图3 主梁自振振型
2.3 船舶撞击力时程荷载
根据船舶在航道内(在航道中心线上)的正常行驶速度、航道中心线至桥墩的距离以及船舶长度等因素综合确定船舶撞击桥梁速度[6],结合武汉天兴洲长江大桥通常航速调查结果及航道水文条件,推算出船舶撞击速度为4.5m/s。根据武汉天兴洲长江大桥设防标准,本文模拟8 000t船舶撞击1号桥塔的第290号节点,撞击角度选取桥轴线法线与撞击速度方向的夹角0 °、10 °、15 °和20 °。针对8 000t船舶,当以4.5m/s速度撞击桥墩时,本文模拟的正撞力时程曲线图如图4所示。
3 桥梁动力响应结果分析
在ANSYS中模拟活载加载有机动法、静力分析和瞬态分析法三种分析方法。在本文中采用瞬态分析法,荷载分140次施加到1号桥塔的290号关键点上,每次施加后进行一次瞬态分析,分析桥梁在规定的时程碰撞荷载下的动力响应问题。在ANSYS完成模型瞬态分析计算后,通过*GET命令提取了1号桥塔塔顶1号节点、主跨跨中1 040号节点横桥向位移。

表1 武汉天兴洲长江大桥自振特性

图4 正撞力时程曲线
3.1 横桥向位移结果提取
提取塔顶1号节点、跨中1 040号节点分别在0°、10°、15°和20°船舶撞击作用下的横桥向位移(图5、图6)。

图5 塔顶1号节点横桥向位移

图6 跨中1040号节点横桥向位移
3.2 结果分析
从图5、图6可以看出,在相同碰撞力作用下,塔顶和跨中的横向位移并非一直单调增大,存在振荡现象,且振荡频率较大。塔顶的横桥向位移随着碰撞角度的改变,其位移曲线变化基本一致。在碰撞历程内,任意相同时刻,横桥向位移几乎相同,即碰撞角度的改变对塔顶的动力响应影响不大。从图7(a)也可以看出,随着碰撞角度的增大,塔顶位移峰值逐渐减小,但减小数值不大,从0~20 °,位移减小约7 %。而在碰撞历程内,随着碰撞角度的变化,桥梁跨中的位移曲线存在较大差别。在相同时刻,不同碰撞角下,位移值存在差值。通过图7(b)也可以看出,随着碰撞角从0 °上升至20 °,位移峰值减小52 %。说明碰撞角的改变对桥梁跨中的动力响应存在较大影响。在桥梁防撞设计中可考虑通过设置增大碰撞角度的防撞装置来减小船舶撞击对桥梁带来的影响。通过横向对比可知,在相同碰撞力作用下,塔顶位移峰值均大于桥梁跨中,说明塔顶响应对于船舶撞击力较为敏感,在实际桥梁防护中应引起重视。
4 结论
本文以武汉天兴洲长江大桥为工程背景,运用ANSYS建立全桥有限元模型。分析桥梁各关键部位在8 000t船舶不同角度撞击下的动力响应,得到以下几点结论:
(1)在碰撞过程中,塔顶和跨中的横向位移并非一直单调增大,存在振荡现象,且振荡频率较大。塔顶的横桥向位移在不同撞击角度下变化规律基本一致,碰撞角度的增加对位移峰值影响不大。
(2)在碰撞过程中,碰撞角度的改变对桥梁跨中位移影响较大,碰撞角度从0°上升至20°,位移峰值减小达52 %。
(3)在相同船舶撞击作用下,塔顶位移峰值远大于跨中,说明塔顶位移响应对于船舶撞击力较为敏感,在实际桥梁防护中应引起重视。
(4)在相同碰撞力作用下,碰撞角度的增大能有效地降低碰撞对桥梁造成的影响。在桥梁防撞设计中,可考虑通过增大碰撞角来降低桥梁结构损坏风险。
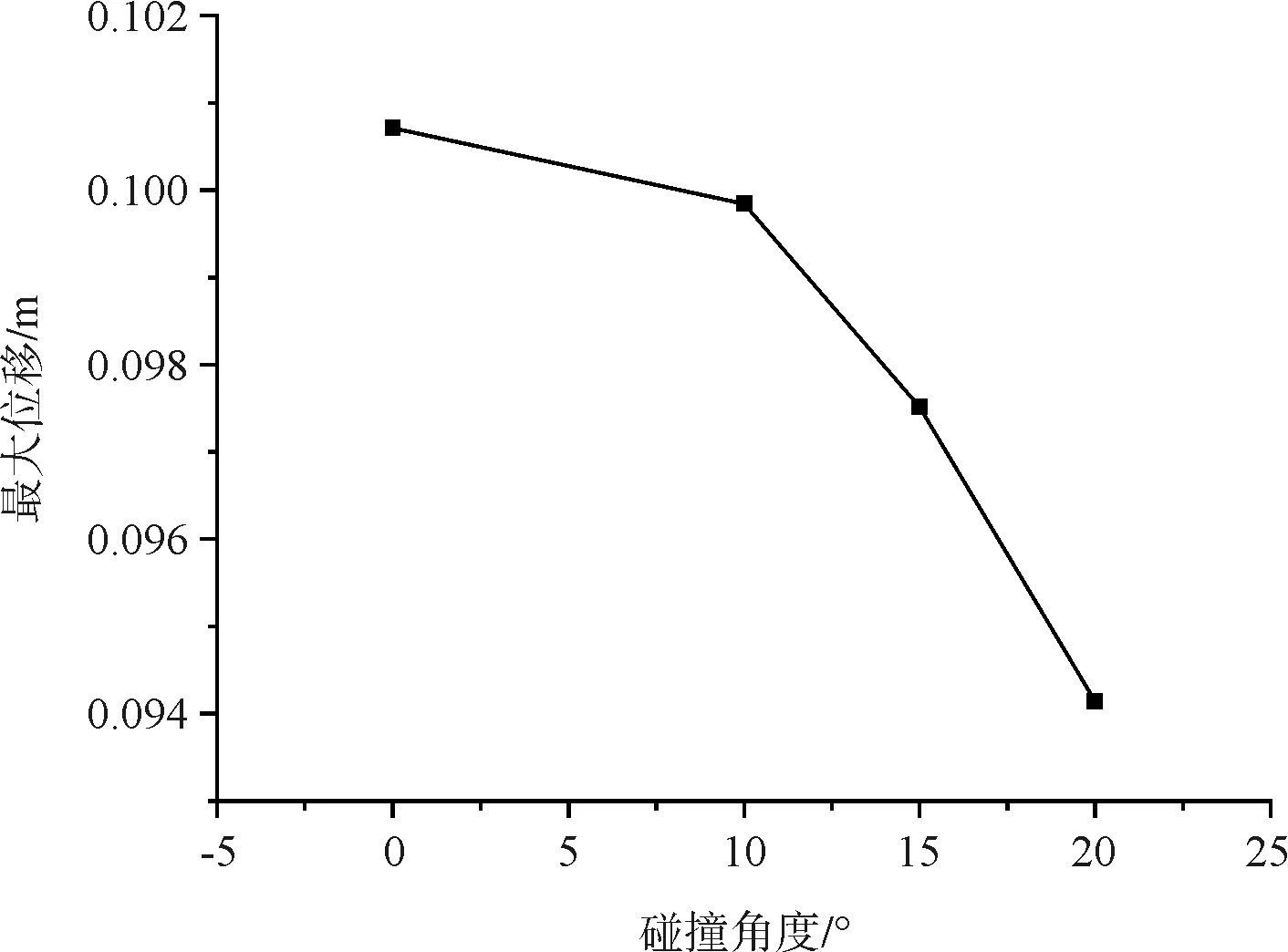
(a) 1号节点

(b)1040号节点图7 横桥向最大位移
