成都地区排桩支护结构对土层参数敏感性分析
2019-07-19吴兵
吴 兵
(核工业西南勘察设计研究院有限公司,四川成都 610061)
排桩支护结构是国内深基坑普遍应用的一种支护形式,在成都地区深基坑工程中有着广泛的应用。在实际工程设计中,根据设计方法求得给定参数值情况下的围护结构的变形和内力,但随着某些参数在取值上可能发生的变化,结构的变形和内力会发生什么样的变化对整个工程的经济和安全有着重要的影响,对实际工程的参数敏感性分析为设计施工决策提供了重要依据。
1 工程概况
1.1 工程特点
成都地铁某广场站深基坑开挖深度约23.54m,采用“排桩+内支撑”支护体系。排桩采用Φ1200@2200mm钢筋混凝土桩,桩长为27m,嵌固深度为3.5m;内支撑采用Φ603×12mm钢管,水平间距2.7~3.5m,竖向设置4道;桩间土体采用Φ8@150mm×150mm钢筋网片加150mm厚C20混凝土防护。明挖基坑标准段围护结构剖面见图1。

图1 基坑标准段围护结构剖面
1.2 工程地质及水文地质条件
站区地处成都平原岷江Ⅲ级阶地,为山前台地地貌。场地范围内上覆第四系人工填土层,第四系中、下更新统冰水沉积(Q2-1fgl)黏土、粉砂、含卵石黏土和含黏土卵石,下伏基岩为白垩系上统紫红色泥岩。
地下水主要有4种类型:一是赋存于黏土层之上的上层滞水,二是赋存于黏土中的裂隙水,三是第四系松散土层(含卵石黏土和含黏土卵石)的孔隙潜水,四是基岩裂隙水(基岩溶孔溶隙裂隙潜水)。
2 有限元数值模拟
2.1 基本假设及计算模型
(1)该工程属于典型的长条型基坑,计算时假设沿基坑长度方向无限长,取其中1根桩及周围土体为研究对象。
(2)由于在基坑开挖时通过降水使地下水位一直处在坑底以下,故不考虑地下水的渗流作用。
(3)不考虑桩间挂网喷射混凝土对桩间土的防护作用。
(4)砂卵石、泥岩采用Mohr-Coulomb模型;黏性土采用线性Drucker-Prager模型;围护桩和钢支撑均采用线弹性本构关系。土体和围护桩采用实体建模,采用C3D8R单元;钢支撑采用仅压杆单元T3D2。
(5)文章采用接触面加摩擦的方式来模拟支护结构与土之间的接触特性,摩擦系数统一取值0.35。

图2 有限元计算网格
整个模型土体共计11 841个单元,支撑40个单元和围护桩1242个单元,桩土界面建立7个接触对。有限元计算网格见图2。
2.2 材料参数选取
(1)土岩的物理力学参数。
为简化计算,对实际地层进行了适当简化,将地层分为黏性土、砂卵石、泥岩3层,根据工程勘察资料,其计算参数见表1。
(1)collection of R.p=p,{R.s}is grouped by different R.s
(2)钢筋混凝土灌注桩。

表1 土(岩)层的计算物理力学参数指标
混凝土强度等级C30,桩身纵筋为25Φ25,钢筋等级为Q235,围护桩的弹性模量E近似取值为30GPa,泊松比υ取值为0.2,密度取值为2 400kg/m3。
(3)钢管内支撑。
弹性模量E取值为210GPa,泊松比υ取值为0.2。
2.3 计算工况
根据基坑开挖和加撑的施工工序,每层土体开挖和加撑均单独作为一个工序,工况划分:开挖至1.5m—加第一道支撑—开挖至7.5m—加第二道支撑—开挖至13.5m—加第三道支撑—开挖至18.5m—加第四道支撑—开挖至23.5m(基底)—拆除第四道支撑。
各道支撑安装完成后,立即施加预加轴力。因论文取1根桩(间距为2.2m)进行计算分析,所以应按支撑水平间距(3.5m)对支撑施加轴力进行折减,折减比为2.2/3.5=0.63。计算模型中预加轴力取值自上而下依次为40kN、200kN、350kN、350kN。
2.4 计算结果分析
选取的计算模型近似于基坑长边中部的围护桩及桩周土体,所以计算结果与基坑长边中部的围护桩的实测结果进行比较分析(图3、图4)。

图3 桩身水平位移计算结果
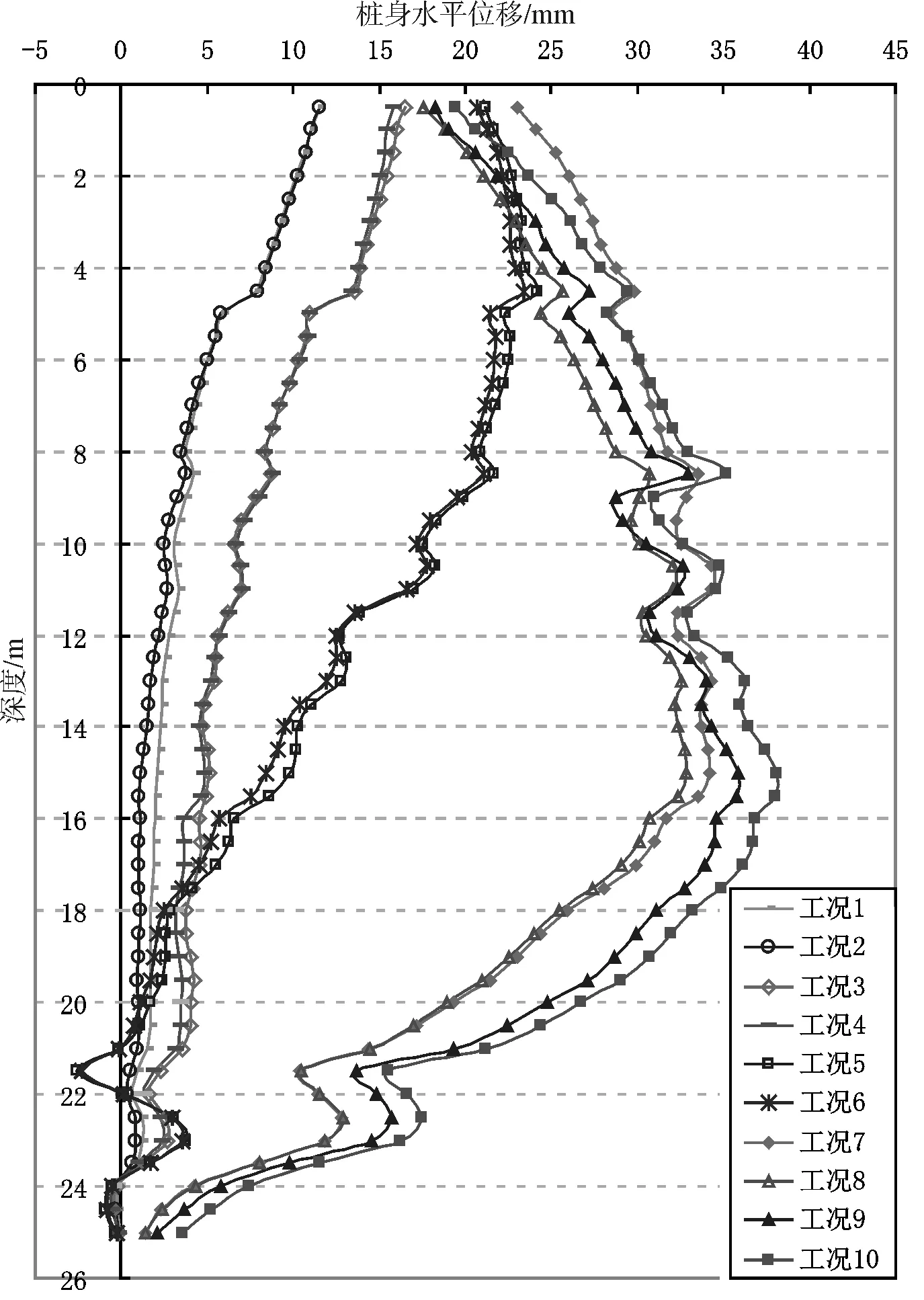
图4 桩身水平位移实测结果
计算结果表明:在开挖第一层土体(工况2)后,由于及时加撑并施加预加轴力,使得桩顶发生向坑外方向的水平位移,随着开挖深度的增大和支撑的设置,桩顶位移不会明显增大,桩身中部向坑内凸出,桩身最大水平位移也相应地逐渐下移,开挖至基坑底部时,最大水平位移发生于桩顶以下约16.0m处,其位移计算值约32.0mm。
比较计算结果和实测结果的桩身水平位移曲线,形状较为相似,呈“鼓肚”形状,计算与实测的桩身最大水平位移及发生位置较为接近。总体而言,计算结果所反映的围护桩的变形趋势与实际较为吻合。
3 土体刚度、强度参数敏感性分析
3.1 参数敏感性分析方法

在实际系统中,由于决定系统各参数是不同的物理量单位,为了比较敏感程度的大小,经常要进行无量纲化处理,绘制ΔF/F*~Δxi/xi*(i=1,2,3,…)曲线,该曲线的斜率绝对值定义为参数敏感性函数:
αi=|ΔF/F*|/|Δxi/xi*|,(i=1,2,3,…n)
参数敏感度函数可以比较系统特性对各参数的敏感程度,敏感度函数值越大,系统特性对该参数越敏感。
为简化计算,假设基坑开挖土体为单一土层,即分别按黏性土和砂卵石进行计算。桩端嵌固于泥岩,内支撑不施加预加轴力,模型的其他尺寸和参数与实际工程一致,统一以基坑开挖至底部这一工况的计算结果进行比较分析。
3.2 黏性土的刚度、强度参数敏感性分析
设定基准状态X*=(x1*,x2*,x3*)=(E,c,φ),系统特征F*=f(X*)=(E,c,φ)。基准值F*=(8,35,16°)。即以基坑开挖土层参数分别为E=8MPa、c=35kPa、φ=16°时计算得到桩体的最大弯矩值、最大水平位移值作为基准值,分析基坑围护桩的变形和内力对上述三个参数的敏感程度(表2)。

表2 黏性土土层参数敏感性分析计算

图5 桩身最大水平位移-土层参数变化率关系

图6 桩身最大弯矩-土层参数变化率关系
由图5、图6的曲线斜率绝对值的大小可以判断:基坑开挖土层均为黏性土时,围护桩的变形及内力对上述3个土层参数的敏感程度大小是φ>c>E。
3.3 砂卵石的刚度、强度参数敏感性分析
设定基准状态X*=(x1*,x2*,)=(E,φ),系统特征F*=f(X*)=(E,φ)。基准值F*=(55, 35°)。即以基坑开挖土层参数分别为E=55MPa、φ=35°时计算得到桩体的最大弯矩值、最大水平位移值作为基准值,分析基坑围护桩的变形和内力对上述两个参数的敏感程度(表3)。

表3 砂卵石土体参数敏感性分析计算
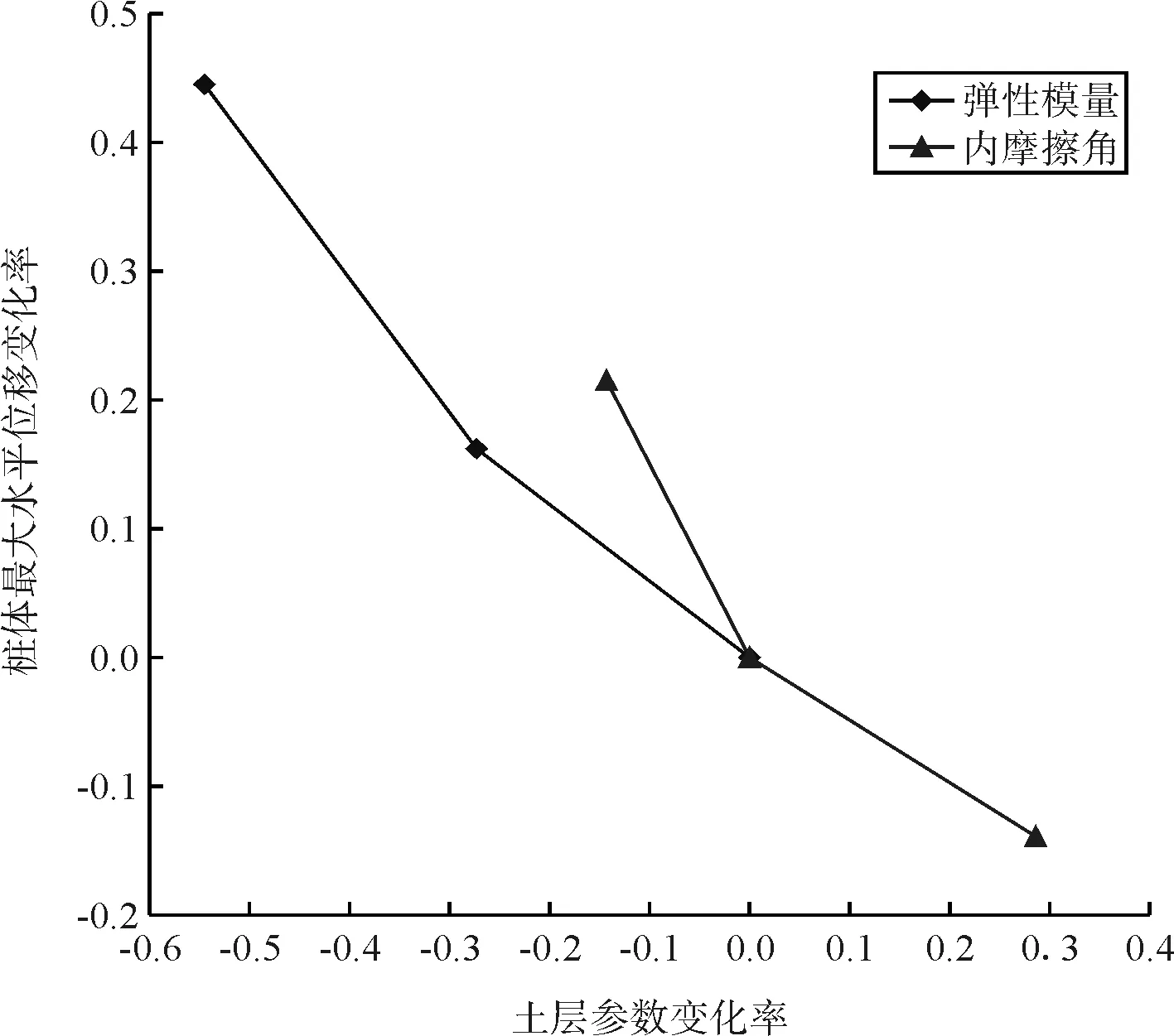
图7 桩身最大水平位移-土层参数变化率关系

图8 桩身最大弯矩-土层参数变化率关系
由图7、图8的曲线斜率绝对值的大小可以判断:基坑开挖土层均为砂卵石时,围护桩的变形及内力对上述2个土层参数的敏感程度大小是φ>E。
3.4 黏性土与砂卵石的刚度、强度参数敏感性比较
由表4、表5可知:土层刚度、强度对桩体内力和变形具有较大的影响,尤其是土体内摩擦角的影响更大,所以在工程实际中,对上述参数的合理取值相当重要,如果取值偏小,将导致设计保守。另外,黏性土的弹性模量和内摩擦角对桩体内力和变形的影响程度明显大于砂卵石。
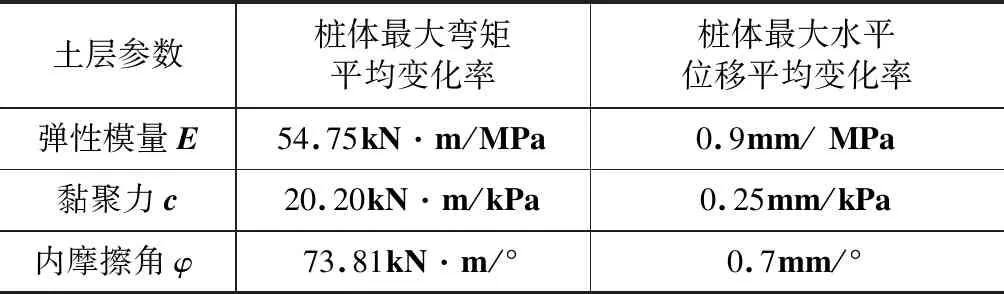
表4 黏性土土层参数对桩体内力和变形的影响
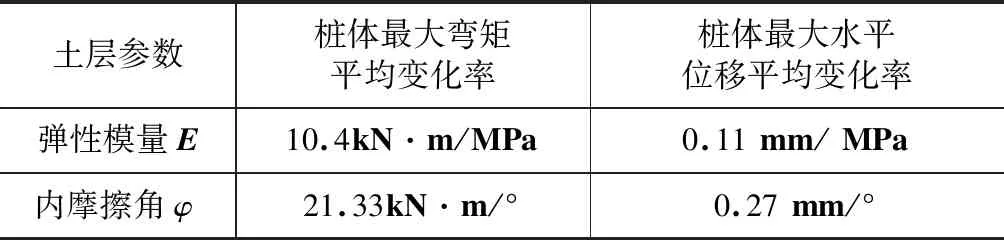
表5 砂卵石土层参数对桩体内力和变形的影响
4 结束语
(1)通过数值模拟计算,并与实测结果对比分析,数值模拟计算结果对参数准确性依赖较大,参数选取不合理可能造成与实际差异较大。
(2)以上对于土层参数敏感性分析可以看出,对于排桩支护结构,围护桩变形及内力影响最大的参数是土体的内摩擦角,因此在设计计算中,确定合理的土体内摩擦角至关重要。
(3)对于黏性土地层,围护桩的变形及内力对土体刚度、强度参数的敏感程度大小分别为φ>c>E;对于砂卵石地层,则为φ>E。另外,黏性土的E和φ对围护桩的变形及内力的影响程度大于砂卵石。
