厦门翔安水底隧道断面形式优化设计研究

秦 昌, 张志强, 周宇锴

(西南交通大学交通隧道工程教育部重点实验室， 四川成都 610031)

水底隧道断面形式合理设计有利于洞室开挖安全、围岩稳定、支护结构的受力合理、减小开挖面积、降低造价、隧道美观、提高行车舒适度等。目前，关于铁路隧道、公路隧道断面设计已有规范规定，尤其铁路隧道已有完整的标准断面供参考设计，公路隧道规范经过修订也对公路隧道横断面内轮廓设计推行标准化。水底隧道的修建在我国隧道建设中属于新兴领域，关于水底隧道断面形式的研究文献鲜见于学术期刊，其设计方法多参照山岭隧道的设计方法，所以，基于流固耦合研究水底隧道断面形式优化对指导水底隧道的设计具有很重要的意义。

本文针对以厦门-翔安海底隧道的工程地质、水文地质及建筑限界为研究基础，基于流固耦合计算理论，计算分析不同断面形式情况下的衬砌结构受力情况，进而进行断面形式优化，以期为类似工程提供指导意见。

1 数值模型

以厦门-翔安海底隧道的工程地质、水文地质及建筑限界为研究基础，通过断面形状的变化，来研究单心拱与三心拱马蹄形断面的受力差别，同时研究三心拱马蹄形断面形式下仰拱曲率半径对隧道结构的影响，进而进行断面形式优化，给出水底隧道中仰拱的主要作用。马蹄形断面设计参数见图1及表1。

图1 马蹄形断面设计参数

编号拱部半径/角度R1/φ1侧墙半径/角度R2/φ2墙脚弧/角度R3/φ3仰拱半径/角度R4/φ4内轮廓面积/m217.4/70.0°7.4/20.00°2.5/34.59°17.50/23.44°120.1127.4/70.0°5.7/25.09°2.5/65.09°17.50/18.77°120.6537.4/70.0°5.7/25.09°2.5/65.09°15.00/22.05°121.9247.4/70.0°5.7/25.09°2.5/47.69°12.50/30.25°123.7857.4/70.0°5.7/25.09°2.5/47.69°10.00/39.03°128.48

数值模拟思路：有限差分模型如图2，支护结构仅考虑初期支护(喷射混凝土+钢拱架)及二次衬砌，不考虑施工过程的影响，即全断面开挖，开挖的同时施加初期支护，计算至收敛准则(最大不平衡率1×10-4)，再施加二次衬砌(图2)。工况设置主要以各断面形式下仰拱排水和封堵为依据。衬砌结构主要荷载有：自重、隧道开挖的释放荷载、渗流体积力作用下围岩的形变压力，以及仰拱封堵时仰拱部位的静水压力。围岩、注浆圈、初期支护及二次衬砌的物理力学参数见表2。

图2 三维有限差分模型

2 结果分析

根据各工况条件下，围岩位移场及围岩塑性区的发展，初期支护和二次衬砌的结构内力及安全系数，孔隙压力场的改变，来分析研究不同断面形式，仰拱曲率半径的影响。

2.1 围岩位移场及围岩塑性区

围岩位移场主要以拱顶及仰拱中心的竖向位移，拱脚的水平位移为研究对象，各工况下的结果列于表3。塑性区的分布见图3。

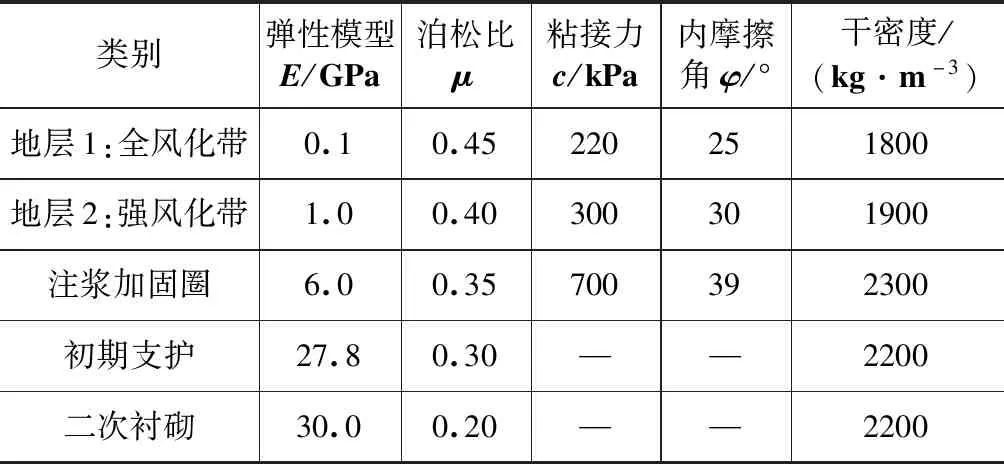
表2 围岩及支护结构物理力学参数

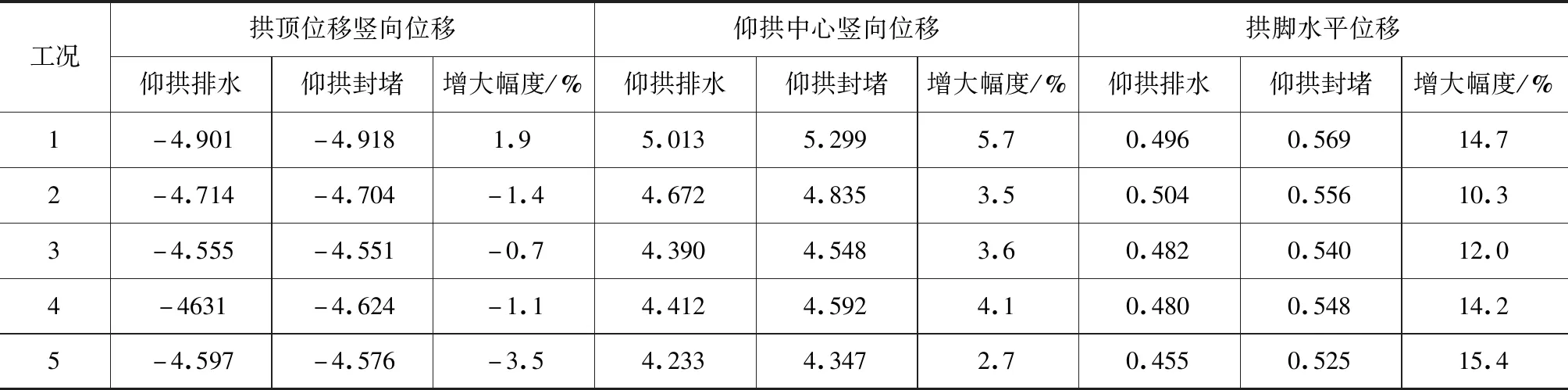
表3 监控点处位移值 mm

(a) 工况1：仰拱排水

(b) 工况1：仰拱封堵

(c) 工况2：仰拱排水

(d) 工况2：仰拱封堵

(e) 工况5：仰拱排水

(f) 工况5：仰拱封堵

通过表3和图3可知：

(1)随着仰拱曲率半径R的减小，洞室周围位移减小，R=10.0m时，洞室拱顶、仰拱中心及拱脚水平位移最小，说明仰拱对控制围岩位移是有效的。

(2)仰拱封堵与仰拱排水相比，两者洞室拱顶位移相差不大，仰拱封堵使仰拱“隆起”值及拱脚水平位移值(外扩)增大，仰拱最大增大幅度为5.7 %，拱脚最大增大幅度为15.4 %。

(3)仰拱曲率半径越小，洞室周围塑性区的深度及面积越小；仰拱封堵时，洞室周围塑性区面积更大，主要是在仰拱位置增大了塑性区的发展，使之处于破坏状态，更不利于隧道洞室底部的稳定。

(4)图3中，工况1与工况2相比，可以发现工况1比工况2在拱肩处塑性区深度要大，说明侧墙弧度半径对塑性区的发展还是有影响的，侧墙弧度半径越小，塑性区深度越小。

2.2 衬砌结构受力分析

为了研究隧道断面形式及仰拱曲率半径对衬砌结构受力的影响，计算各工况仰拱排水与仰拱封堵下，初期衬砌及二次衬砌的轴力、弯矩及安全系数。限于篇幅，本文仅列出工况1仰拱排水时与仰拱封堵时的初衬的内力图，如图4和图5所示。

通过对初期衬砌及二次衬砌的轴力、弯矩及安全系数的数据及受力形式的分布比较，可以得出：

(1)仰拱设置为排水或封堵时，初衬在仰拱位置的受力表现为：随着仰拱曲率半径R的减小，初衬的弯矩减小、轴力增大，安全系数降低；初衬在拱部及侧墙的受力表现为：随着仰拱曲率半径R的减小，初衬弯矩及初衬轴力减小，更有利于拱部及侧墙的受力。

(2)仰拱封堵与仰拱排水相比，初衬在仰拱位置的弯矩较小、轴力较大、安全系数较小，说明仰拱封堵不利于隧道洞室仰拱处衬砌结构的受力；而在拱部及侧墙位置两者弯矩、轴力及安全系数相差不大。

(a) 初衬弯矩(单位：kN·m)

(b) 初衬轴力(单位：kN)图4 仰拱排水时工况1初衬的轴力和弯矩

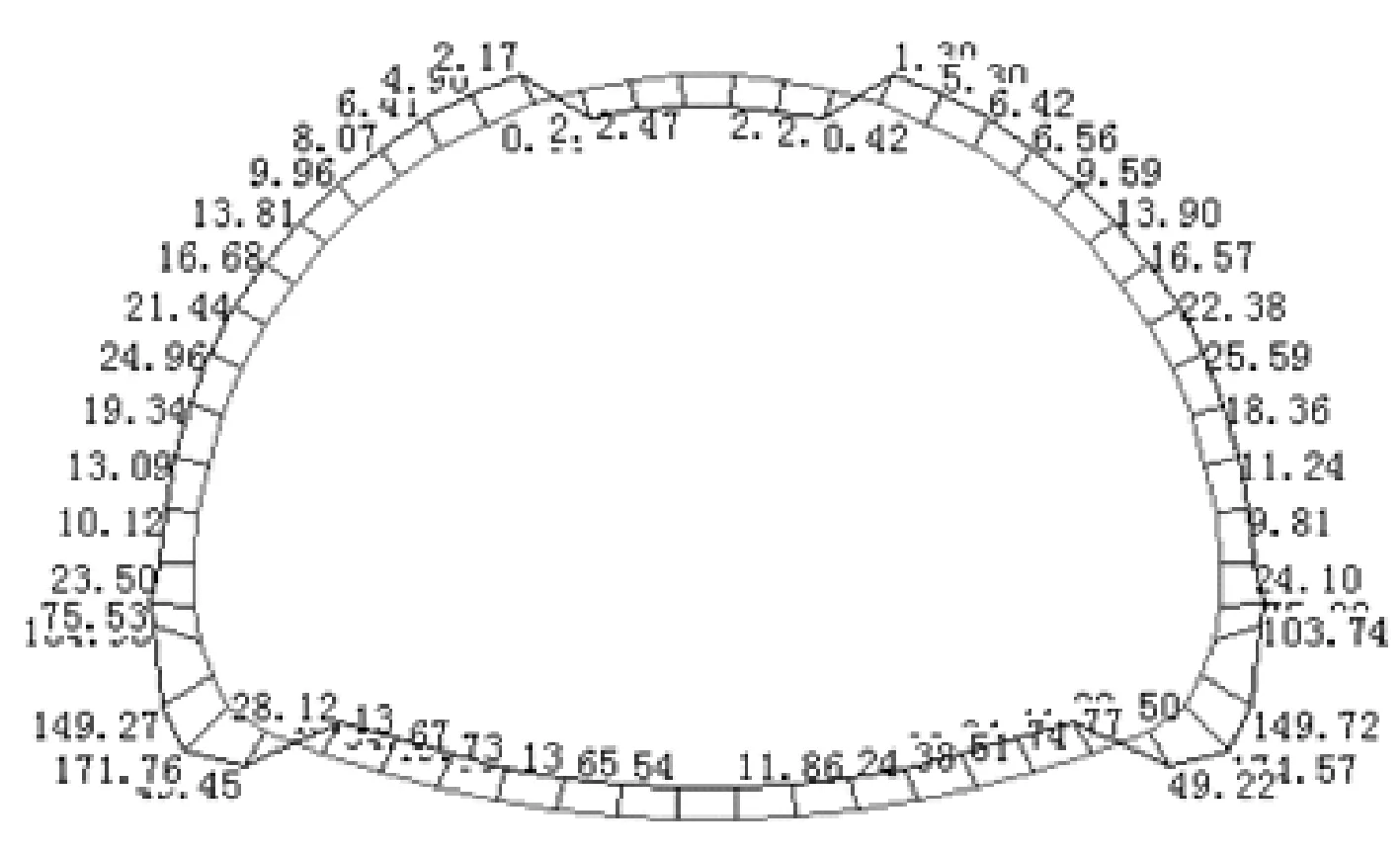
(a) 初衬弯矩(单位：kN·m)

(b) 初衬轴力(单位：kN)图5 仰拱封堵时工况1初衬的轴力和弯矩

(3)二衬的受力形式：拱部及仰拱位置均为内侧受拉，侧墙位置内侧受压；仰拱曲率半径R对二衬的受力影响不明显，拱部及仰拱位置为二衬的薄弱部位，侧墙很安全，工况2(R=17.5m)时，仰拱及拱部的安全系数最大。

(4)二衬施设以后，仰拱封堵与仰拱排水相比，由于封堵边界设置在初衬内边缘，所以仰拱封堵时，二衬仰拱及侧墙位置安全系数提高，但拱顶附近安全系数降低。

(5)工况1(单心圆)与工况2(三心圆)相比，两者结构受力差别不大，相比而言，工况1拱部受力较好，但墙脚及仰拱处受力较差；如果侧墙与仰拱位置能用较圆顺的圆弧连接，单心拱断面形式还是可行的。

3 结论

本文主要从公路隧道建筑限界与隧道断面之间的几何关系，给出了马蹄形隧道断面几何设计参数，从数值模拟角度对马蹄形断面拱部为单心圆或三心圆时，衬砌结构的受力进行了研究，以及研究分析了三心圆马蹄形断面下仰拱曲率半径对围岩位移场、衬砌结构受力的影响，从而明确水底隧道断面优化的思路和原则。综合分析，得出以下主要结论：

(1)隧道断面采取单心圆与采取三心圆相比，前者隧道开挖面积偏大，塑性区深度较大，墙脚处受力较差；故断面优化时，侧墙所采用的半径在保证能与拱部及拱底顺滑连接的前提下，应比拱部半径小。

(2)仰拱曲率半径对控制围岩位移，改善衬砌结构的受力是有益的，一般表现为：随着仰拱曲率半径R的减小，洞室周围位移减小，初衬在仰拱位置受力增大、安全系数降低，在拱部及侧墙受力减小、安全系数增大；随着仰拱曲率半径R的减小，二衬在仰拱部位安全系数相应提高。

(3)仰拱位置防水措施的设置对围岩位移场、塑性区、渗流场、结构受力均有很大影响，主要表现为：仰拱封堵时，仰拱处“隆起”值增大、仰拱处塑性区面积及深度增大，同时初衬背后孔隙水压力值恢复初始水压力值大小，二次衬砌结构要在仰拱位置承受初始水头大小的静水压力作用。故，断面优化设计时，仰拱处一定要设计成能承受较大静水压力作用的圆弧，其曲率半径越小，二次衬砌结构受力越合理、安全系数越高。

(4)水底隧道断面优化设计的主导思想：首先，根据建筑限界确定拱部及侧墙圆弧半径；其次，根据仰拱位置防排水措施对空间的要求，同时保证能用较小半径(R=100～250mm)的圆弧使其与侧墙圆滑连接来设计仰拱曲率半径；最后，利用流固耦合对该隧道断面下的衬砌结构进行分析，以满足结构安全要求。