基于机器学习的供热系统热负荷多步递归预测

薛普宁， 周志刚， 蒋 毅， 陈 昕， 方修睦， 刘 京

(1.哈尔滨工业大学 建筑学院， 黑龙江 哈尔滨 150006； 2.哈尔滨工业大学，寒地城乡人居环境科学与技术工业和信息化部重点实验室， 黑龙江 哈尔滨 150006；.黑龙江省计算中心， 黑龙江 哈尔滨 150026)

1 概述

集中供热是保障人民生产生活的重要基础能源设施。近年来，在我国能源战略转型的大背景下，随着智慧城市、“互联网+”智慧能源等概念的提出，供热行业也兴起了智慧供热的研究浪潮[1]。智慧供热是以数字化、网络化、智能化的信息技术设施为基础，以用户为目标，以低碳、舒适、高效为主要特征，以透彻感知、广泛互联、深度智能为技术特点的现代供热方式[2]。其内涵是利用传感器透彻感知供热系统信息，网络传输信息全面互联互通，以及系统实现智能决策和智能控制。

热负荷的准确预测是实现供热系统运行控制、决策优化，提高供热效率，降低运行维护成本的重要前提。由于供热系统具有规模庞大、结构复杂、热惰性高等特点，难以通过数学建模方法建立有效的热负荷预测模型。机器学习通过从数据中学习模型从而赋予计算机在特定任务上的预测或决策能力。随着数据存储与计算机技术的飞速发展，机器学习在科研和商业领域得到广泛的应用，也为热负荷预测提供了新的思路。供热企业在供热系统的运行管理过程中，储存了大量的历史运行数据，这些数据反映了供热系统潜在的运行特性，使得采用机器学习算法建立热负荷预测模型成为可能。

国内外已有许多学者开展了机器学习算法在热负荷预测领域的应用研究，常用算法包括多元线性回归[3]、自回归积分移动平均[4]、支持向量回归[5]、极限学习机[6]、回归树[7]、梯度提升[8]、神经网络[9]等。然而，目前的研究多集中于热负荷的单步预测，模型输出结果为未来某一时刻的热负荷预测值。实现供热系统的决策控制，需要提前掌握未来一段时期内的热负荷的动态概况，即对热负荷进行多步预测。

为了实现供热系统热负荷的多步预测，本文提出了一种基于机器学习的供热负荷多步递归预测策略，利用支持向量回归(support vector regression，SVR)、极限梯度提升(extreme gradient boosting，XGBoost)分别建立了热负荷单步预测模型，并根据实际供热系统案例对所提出的多步递归预测策略的预测性能进行了评估。本文中所有模型均通过R语言予以实现。

2 研究方法

2.1 用于热负荷预测的数据集

热负荷预测属于机器学习中的监督学习。监督学习的任务是训练一个模型，使得模型能够对给定的输入变量，对其相应的输出变量做出一个好的预测。这里的输入变量指热负荷的影响因子，输出变量是要预测的目标时刻的热负荷。在机器学习中，模型的每一个输入变量被称为一个特征或属性，而模型要预测的目标变量则被称为标签。一个由特征和标签所组成的向量，被称为一个样本或示例。一组样本构成的集合称为数据集[10]2-3。

一般地，我们用x=(x1,x2,…,xd)T表示一个样本的所有特征组成的向量，称为特征向量，d称为样本的维数；用y表示样本的标签；用D={(x1,y1),(x2,y2),…,(xn,yn)}表示包含n个样本的数据集[10]2-3。

热负荷的影响因子可分为4类：时间变量、气象参数、系统运行数据和社会因素(用户行为)[4, 11]。时间变量即年、月、日、小时等参数；气象参数包括室外空气温湿度、太阳辐射、风速等，是热负荷最显著的影响因子；系统运行数据是反映供热系统运行状态的供回水温度、流量、供热量、控制信号等变量；社会因素指热用户的用热模式、社会活动、自主调节等行为。虽然热负荷的影响因子很多，相关研究表明，只需选择少数关键的影响因子如时间、室外空气温度、历史供热量(热负荷)作为热负荷预测的数据集的特征，就可以得到较准确的热负荷预测结果[12]。

考虑到目前我国供热系统缺少对用户行为的连续监测记录，而且气象参数中也一般只记录室外空气温度，本文只选择时间变量、室外空气温度和历史热负荷这3种类型的热负荷影响因子作为热负荷预测中特征向量的特征。

2.2 热负荷单步预测模型

本文提出的热负荷多步递归预测策略是对热负荷单步预测模型的拓展，因此首先给出热负荷单步预测模型的介绍。

热负荷单步预测模型是利用特征向量预测样本的标签，即预测未来目标时刻的热负荷值。该模型可用式(1)表示[13]:

(1)

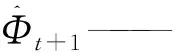
f——热负荷单步预测模型

t——时刻

Tt+1——t+1时刻室外空气温度的预报值

Φt——t时刻热负荷的真实值

Φt-1——t-1时刻热负荷的真实值

Φt-(m-1)——t-(m-1)时刻热负荷的真实值

m——特征向量中历史热负荷的总数目

2.3 热负荷多步递归预测策略

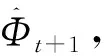
2.4 热负荷多步递归预测的流程

图2为热负荷多步递归预测的流程。该流程可分为4个步骤：数据预处理、数据集划分、模型训练和模型评估。

2.4.1 数据预处理

数据预处理可细分为3个子步骤：特征选择、特征工程和特征变换。通过数据预处理将用于热负荷预测的数据集变换为SVR模型和XGBoost模型所要求的格式。

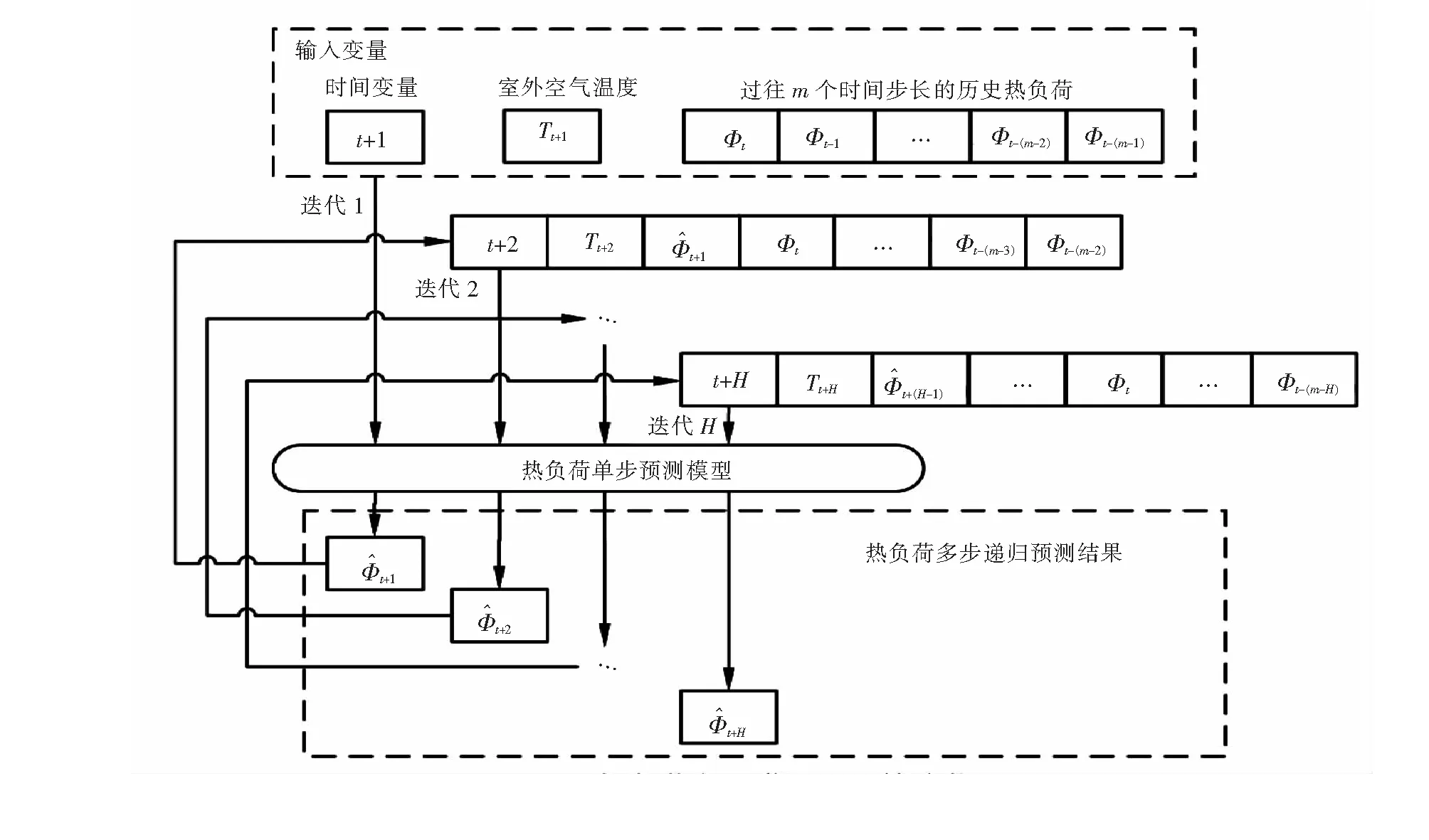
图1 热负荷多步递归预测策略

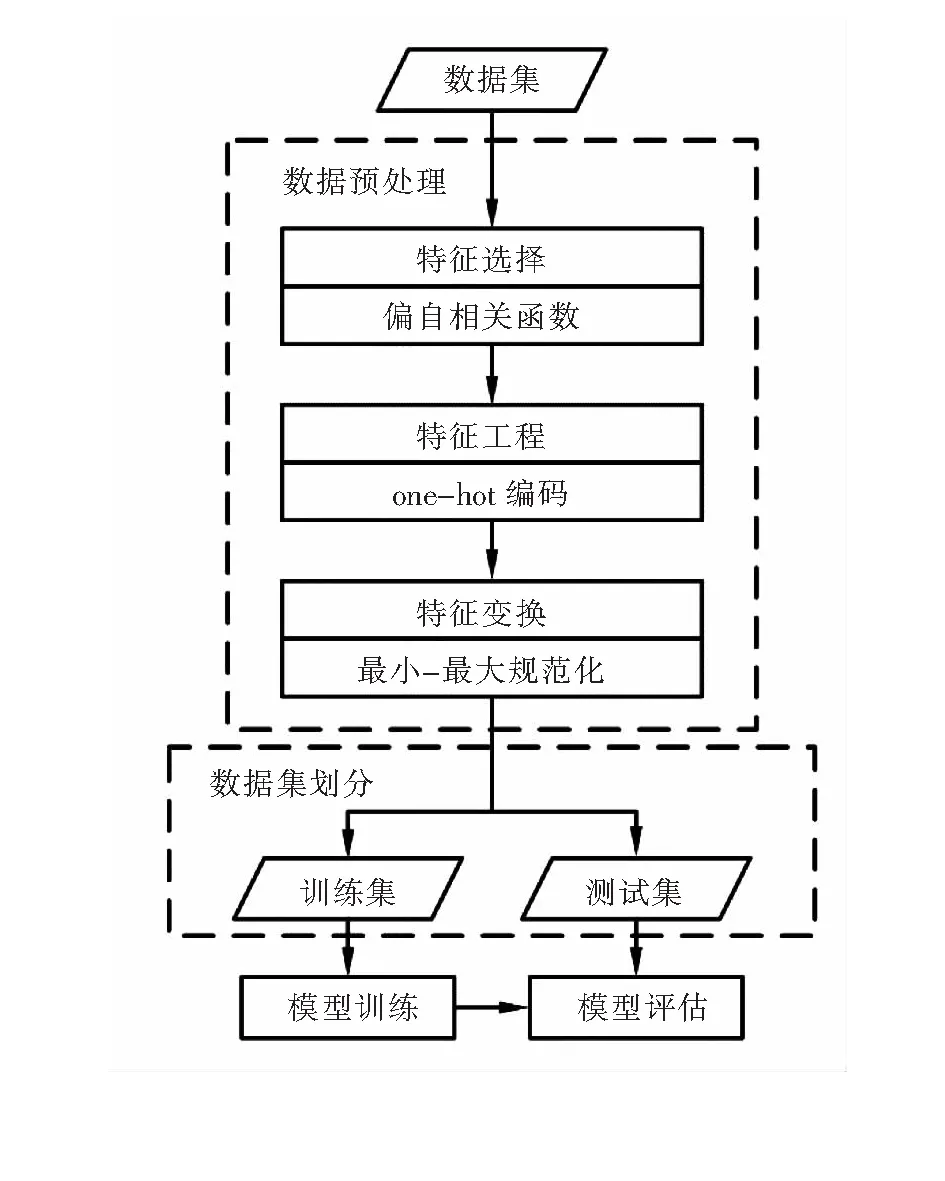
图2 热负荷多步递归预测的流程

特征选择旨在确定数据集的特征向量中历史热负荷的总数目m。本文采用偏自相关函数(partial autocorrelation function,符号为P)对热负荷时间序列进行分析以确定最优的m值。对于一个热负荷时间序列，偏自相关函数移除当前值Φt与历史值Φt-i之间的所有变量Φt-1，Φt-2，…，Φt-i+1带来的影响后，度量Φt和Φt-i的相关性[14]。若P绝对值超过显著性水平，表明历史值与当前值具有很强的相关性，则可将该历史值用作样本的一个特征。在本文的特征选择中，当热负荷时间序列的P绝对值不再大于显著性水平时，对应的m值的最大值作为最终的m值。

特征工程旨在将类别特征变换为数值特征。SVR和XGBoost均要求输入变量为数值特征。本文在特征工程中采用one-hot编码(one-hot encoding)方法。对于一个有k个类别取值的类别特征，one-hot编码用长度为k的二元向量对k个类进行编码，二元向量的每个元素与每个类一一对应，当类别取值为i时，相应的二元变量的第i个元素为1，其余元素均为0[15]。

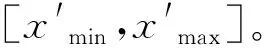
(2)

式中x′——经特征变换后，一个特征的特征值的新值

x——一个特征的特征值的原值

xmin——一个特征的原取值区间的下限

xmax——一个特征的原取值区间的上限

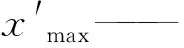
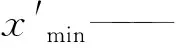
2.4.2 数据集划分

经数据预处理后的数据集，本文采用留出法(hold-out)直接将其划分为两个互斥的子集，其中一个子集用作训练集，另一个作为测试集。我们在训练集上建立热负荷单步预测模型，然后在测试集上，利用所提出的多步递归预测策略预测热负荷，然后对预测结果进行评估。

2.4.3 模型训练

本文分别采用SVR模型和XGBoost模型建立热负荷单步预测模型。SVR模型在之前有很多成功的应用，因此本文选择SVR作为基准模型以评估后续热负荷预测的结果。

① SVR模型

SVR是用于回归任务的支持向量机模型[10]121-145。学习目标是基于训练集在输入空间中得到一个超平面，使得预测变量的真实值与超平面对应的预测值的偏差尽可能小。对于热负荷预测这种在输入空间中的非线性可分问题，SVR通过引入核函数，将样本的特征向量由输入空间映射到更高维度的特征空间中，使得非线性可分问题转换为在高维特征空间中的线性可分问题。SVR模型可表示为：

(3)

式中fsvr——SVR模型

ws——SVR的超平面的法向量

φ——将特征向量由原输入空间映射到高维特征空间的核函数

b——SVR的超平面的位移项

本文中，核函数φ采用高斯核函数，其计算公式为:

(4)

式中κ——高斯核函数

σ——高斯核函数的带宽参数

SVR模型的训练可以形式化为一个凸二次规划问题，优化目标是结构风险最小化，优化变量是ws和b[10]121-145。如果ws和b的某一取值使得式(5)取得最小值，那么此时ws和b的取值称为该优化问题的最优解，该最优解对应的超平面即为最终的SVR模型。

(5)

(6)

式中 C——正则化常数

lε——不敏感损失函数

ε——不敏感损失参数

②XGBsoot模型

XGBoost是一种提升树模型，属于集成学习技术，通过构建并结合多个基学习器来完成学习任务。XGBoost模型采用的基学习器为回归树，即XGBoost模型是多个回归树组成的集合[16]，可用式(7)表示:

(7)

fcart——回归树

K——回归树的总数目

对于一棵具有N个叶结点的回归树，设w=(w1,w2,…,wN)T为叶结点的权重向量，可以用函数q:x→{1,2,…,N}描述回归树的内部结构，函数值q(x)表示样本被划归到的叶结点的索引值。如式(8)所示，函数q和叶结点权重向量w描述了一棵回归树的所有预测信息。回归树的复杂度函数Ω可用式(9)表示。

fcart(x)=wq(x)

(8)

(9)

式中w——权重向量w中的一个元素，表示回归树中一个叶结点的权重值

Ω——描述回归树的复杂度的函数

γ——损失函数值减少的最小阈值，为常数

λ——叶结点的权重向量的L2正则化项

XGBoost模型训练的优化目标函数为[16]：

(10)

式中J——目标函数值

l——损失函数

XGBoost模型的训练采用基于加性模型的训练策略，依次训练每一棵回归树。第z轮模型训练时，保持已训练的回归树fcart,1，fcart,2，...，fcart,z-1不变，然后训练新的回归树fcart,z，如果回归树fcart,z可以优化目标函数J，则将fcart,z加到XGBoost模型中。该过程循环进行，直到XGBoost模型包含K个回归树。对于热负荷预测任务，损失函数l一般为均方误差，因此，优化目标函数式可改写为[16]：

(11)

(12)

(13)

Ij={i|q(xi)=j,j=1,2,…,N}

(14)

式中J(z)——第z轮模型训练时的目标函数值

Ij——划分到回归树中第j个叶结点的所有样本的索引值的集合

g——损失函数l的一阶导数

h——损失函数l的二阶导数

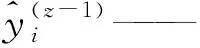
2.4.4 模型评估

当模型训练结束后，利用建立的基于SVR的热负荷单步预测模型和基于XGBoost的热负荷单步预测模型，采取图1所示的热负荷多步递归预测策略，分别对测试集中的样本，预测其热负荷，并对热负荷的预测结果进行评估。

本文采用平均绝对误差(mean absolute error，MAE)和平均绝对百分误差(mean absolute percentage error，MAPE)对热负荷预测的结果进行评价。两个指标的计算公式为：

(15)

(16)

式中IMAE——平均绝对误差

IMAPE——平均绝对百分误差

IMAE和IMAPE值越小，表明热负荷的预测结果越精确；反之，则表明热负荷的预测结果越差。

3 案例分析

本文收集了长春市某集中供热系统热源首站2017年12月22日至2018年3月7日的运行数据，数据采集的时间步长为1 h。用于热负荷预测的数据集包含2个时间变量(月份和小时)、室外空气温度以及逐时热负荷。表1为逐时热负荷和室外空气温度的统计概况。我们采用热负荷多步递归预测策略，按照图2的流程，对该供热系统未来24 h的逐时热负荷进行预测，即预测范围H=24。

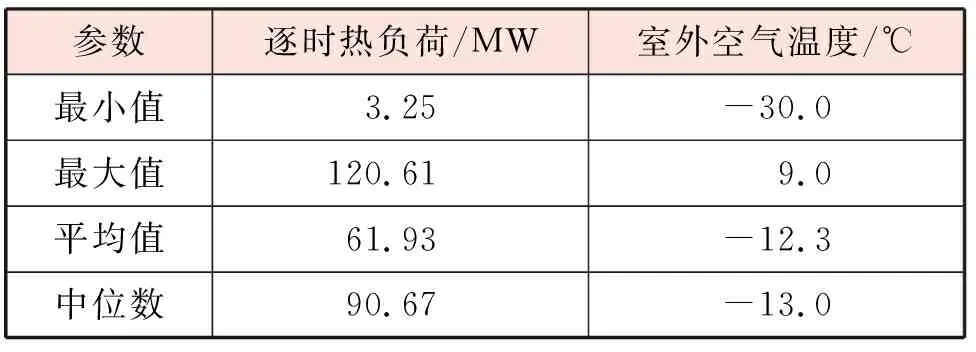
表1 逐时热负荷和室外空气温度概况

首先通过特征选择步骤确定用作模型输入特征的历史热负荷的总数目m。图3为逐时热负荷时间序列的偏自相关分析结果。我们将显著性水平设置为0.15。如图3所示，当时间超过24 h后，P绝对值不再大于0.15，也就是说滞后时间超过24 h的历史热负荷与热负荷当前值的相关性很小。因此，我们设定用于模型输入特征的历史热负荷数目m=24。

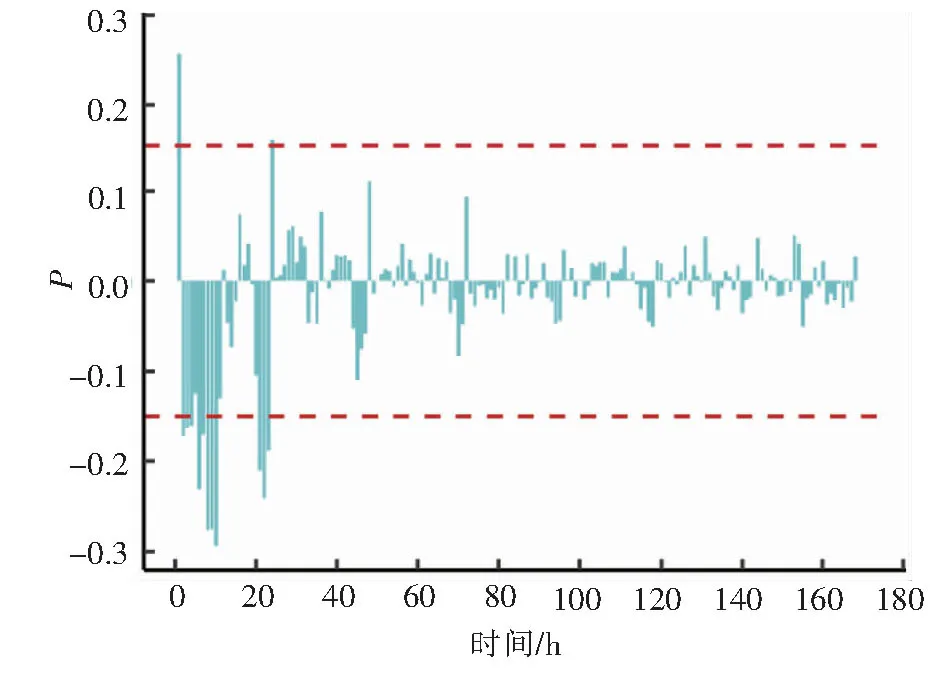
图3 逐时热负荷时间序列的偏自相关分析结果

然后通过特征工程对类别特征月份和小时进行处理，采用one-hot编码将月份和小时分别变换为数值特征。然后使用最小-最大规范化，把所有的数值特征映射到新的取值区间[0, 1]内。最终，通过数据预处理，数据集共包含53个特征。

我们将预处理后的数据集进行划分，其中训练集包含61个供暖日的数据，测试集包含14个供暖日的数据。

在训练SVR模型和XGBoost模型时，需要设定一些参数，参数配置不同，建立的模型的性能往往有显著差别。这些参数的设定过程称为超参数优化。本文对SVR模型的3个超参数进行优化，包括正则化常数C、不敏感损失参数ε、高斯核函数的带宽参数σ。对XGBoost模型的4个超参数进行优化，包括回归树的总数目K、回归树的深度dcart、训练过程中的样本的子采样率r以及学习率η。回归树的深度dcart控制回归树中根节点到叶结点的路径的最大长度；子采样率r描述XGBoost模型的训练过程的随机性；学习率η又被称为收缩因子，其作用是在XGBoost模型的每一轮训练过程中，调节新添加的回归树的权重向量在XGBoost模型中所占的比例[16]。

我们采用10折交叉验证和网格搜索方法在训练集上确定最优的超参数。SVR和XGBoost的超参数优化结果见表2。根据超参数优化结果，在训练集上学习得到最终的热负荷单步预测模型。

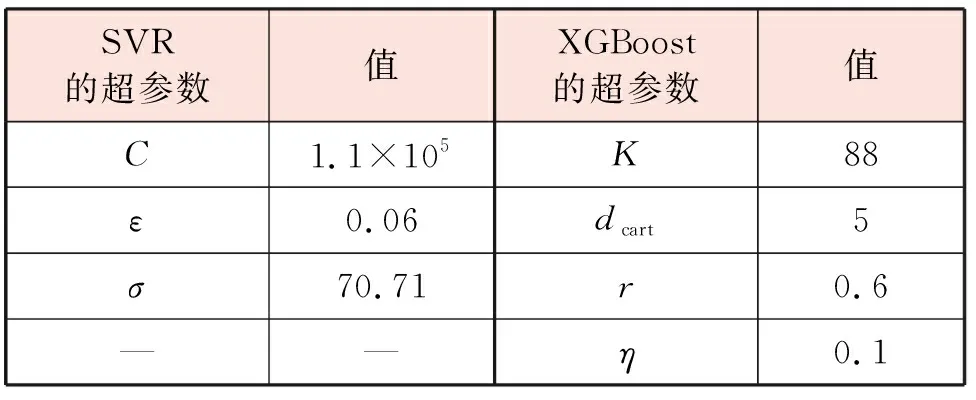
表2 SVR和XGBoost的超参数设置

4 结果与讨论

采用图1所示的热负荷多步递归预测策略，利用建立的基于SVR的热负荷单步预测模型和基于XGBoost的热负荷单步预测模型，依据测试集中14个供暖日的样本，分别对该供热系统在这14个供暖日的逐时热负荷进行预测，并采用式(15)和式(16)对预测结果进行评估。

表3给出了基于SVR的热负荷多步递归预测策略和基于XGBoost的热负荷多步递归预测策略在测试集上的总预测精度，图4描绘了两个模型在其中某一个测试供暖日的详细预测结果。由图4可知，基于SVR的热负荷多步递归预测策略和基于XGBoost的热负荷多步递归预测策略均可以对未来24 h的逐时热负荷进行准确预测，且基于XGBoost的热负荷多步递归预测策略的预测精度要高于基于SVR的热负荷多步递归预测策略的预测精度。

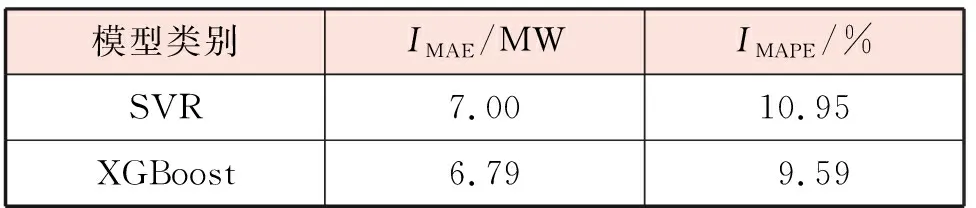
表3 SVR和XGBoost在测试集上的热负荷多步递归预测精度的总预测精度

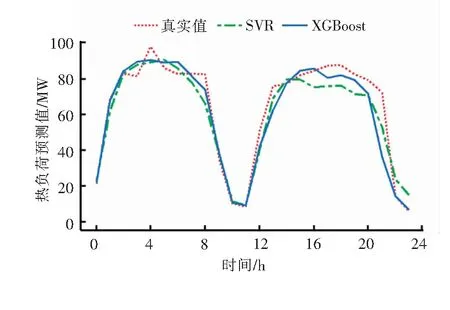
图4 SVR和XGBoost在某测试日的逐时热负荷多步递归预测结果

我们进一步对基于SVR的热负荷多步递归预测策略和基于XGBoost的热负荷多步递归预测策略的预测稳定性进行评估。针对SVR和XGBoost在每个测试供暖日的预测结果，我们绘制其预测精度的箱线图，见图5。箱线图可以度量预测精度的散布程度。由图5可知，XGBoost在这14个测试供暖日的预测精度的分布更加集中，这表明基于XGBoost的热负荷多步递归预测策略在预测稳定性方面优于基于SVR的热负荷多步递归预测策略。

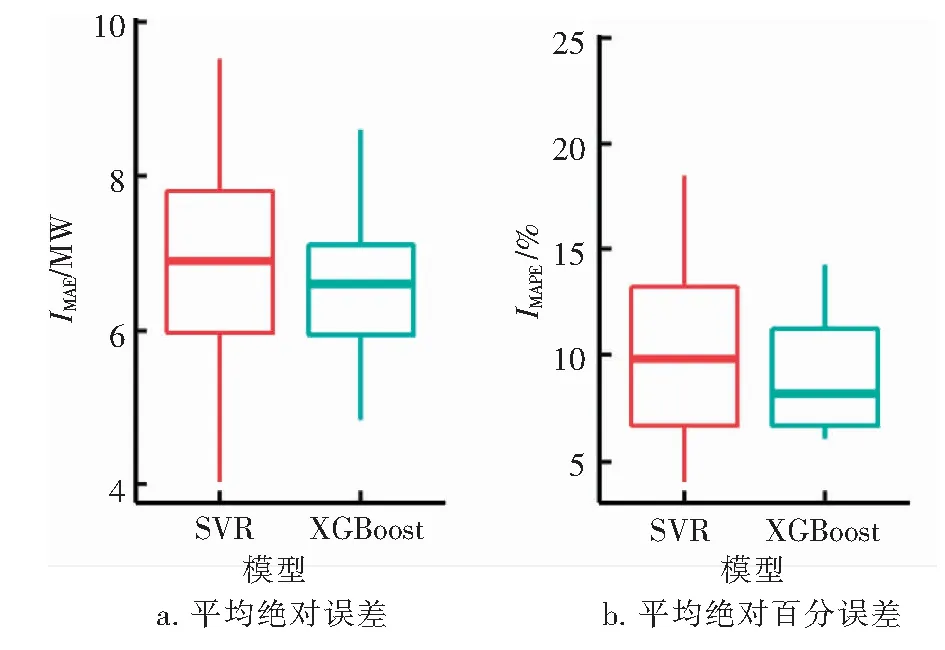
图5 SVR和XGBoost的逐时热负荷多步递归预测精度的箱线图

XGBoost模型通过将多个学习器进行结合，往往可以获得比单一学习器更优越的泛化性能。从预测精度和预测稳定性角度看，XGBoost模型更适用于热负荷多步递归预测任务。也就是说，通过将多个回归树的预测结果集成，XGBoost模型可以在热负荷多步递归预测任务中取得比SVR模型更好的预测结果。

如2.3节所述，热负荷递归预测策略是对热负荷单步预测模型的拓展。在热负荷预测过程中，递归地调用单步预测模型有可能会产生误差累积，导致预测结果的精度随着预测范围H的增大而降低。为分析热负荷多步递归预测的误差累积程度，我们计算了基于SVR的热负荷多步递归预测策略和基于XGBoost的热负荷多步递归预测策略，在这14个测试采暖日中各时刻预测结果的IMAE的平均值，结果见图6。通过图6可以看出，对于本文中预测未来24 h的逐时热负荷概况的案例，随着时间的变化，预测结果的IMAE值的平均值始终在7.5 MW左右波动。表明基于SVR的热负荷多步递归预测策略和基于XGBoost的热负荷多步递归预测策略均不会产生明显的误差累积，在预测范围的各时刻均可以得到较为准确的热负荷预测值。

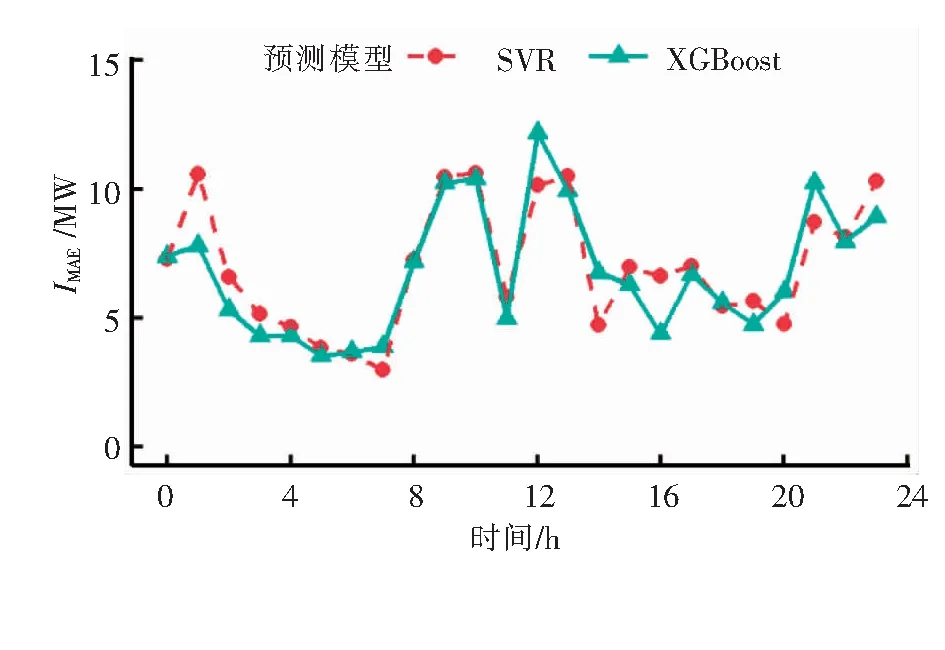
图6 SVR和XGBoost在各时刻预测结果MAE的平均值

5 结论

为实现集中供热系统的运行优化和决策控制，有必要对热负荷的动态概况进行预测。本文提出了一种基于机器学习的热负荷多步递归预测策略，该策略是对热负荷单步预测模型的拓展。详细介绍了热负荷多步递归预测的流程，该流程可分为数据预处理、数据集划分、模型训练和模型评估4个步骤。为评估所提出的热负荷多步递归预测策略的适用性，收集了某供热系统热源首站2017年12月22日至2018年3月7日的运行数据。按照热负荷多步递归预测的流程，分别使用SVR模型和XGBoost模型建立了热负荷单步预测模型，利用所建立的单步预测模型，按照提出的热负荷多步递归预测策略，对该供热系统未来24 h的逐时热负荷概况进行了预测，并从多方面评估了热负荷多步递归预测策略的预测性能。主要结论如下：

① 在预测精度和预测稳定性方面，基于XGBoost的热负荷多步递归预测策略均优于基于SVR的热负荷多步递归预测策略。

② 基于SVR的热负荷多步递归预测策略和基于XGBoost的热负荷多步递归预测策略不会产生明显的误差累积，在预测范围内，各时刻的预测结果均可以满足工程精度要求。

③ 热负荷多步递归预测策略可以实现对供热系统短期热负荷的动态概况的准确预测，为供热系统的运行优化和决策控制提供技术支撑。