基于PCA-GRNN模型的原油管道减阻剂减阻率预测研究

王一斌

（中国石油工程建设有限公司，北京100101）

在进行原油长距离输送的过程中，一般会加入一定量的减阻剂，该种原料可以增加管道的输送能力。近些年来，随着我国社会对油气能源需求量的不断增加，原油管道的输量要求也不断升高，减阻剂也得到了大面积的推广。该种化工原料主要是通过降低管道内原油的摩阻损失，从而使输送能力得以提高，该种原料的使用，间接给油气管道公司带来了经济利益[1]。但是，由于减阻剂的作用原理并不明确，国内外专家并没有形成一致结论，因此，使得减阻剂减阻率的计算成为了一项难题。

目前，国内外专家对减阻剂减阻率的计算问题进行了大量的研究。国外学者Frank Vejahati 等[2]人在考虑数学中π定理的基础上，考虑管道内减阻剂的浓度以及雷诺数因素，提出了一种减阻剂减阻率的计算方法，但是由于该种计算方法所考虑的减阻率影响因素并不全面，所以使得减阻率的计算结果误差较大；国外学者Karami 等[3]人考虑了影响减阻率的各种因素，提出了一种完善的减阻剂减阻率计算方法，但是由于该方法中的某些参数难以测量，使得该模型无法得到有效的利用。除了上述两种方法外，国内外学者还提出了倒数方程法、负指数法等，但是这些方法都存在计算误差较大的问题。

近些年来，人工智能在石油领域得到了大面积的推广，使用智能算法对减阻剂减阻率进行预测也是未来的发展趋势之一。因此，本次研究将综合分析减阻剂减阻率的影响因素，并使用PCA（主成分分析）算法对影响因素进行降维，使用GRNN（广义回归神经网络）算法对减阻剂减阻率进行预测，并将预测结果与其他方法的计算结果进行对比，以此证明该方法的可行性，从而促进人工智能算法在该领域的发展。

1 减阻剂减阻率影响因素初选

1）加剂浓度

目前的研究结果显示，加剂浓度是影响减阻剂减阻率的主要因素。一般情况下，随着加剂浓度的不断增加，减阻率也会不断增加，但是当加剂浓度达到某一数值时，减阻率将趋于平稳不再增加。因此，如果在管道内加入的减阻剂浓度相对较小，则无法充分发挥减阻剂的作用，如果加入的减阻剂浓度过大，会造成一定的浪费[4]。

2）管道基本参数

减阻剂是通过降低管道内原油的摩阻损失，达到增输的效果，而摩阻损失又和管道的管径、长度以及管道管壁粗糙度具有一定的联系，因此，这三项因素也可能会对减阻率产生影响[5]。但是由于管道管壁粗糙度数据难以准确测量，因此，在本次研究中使用管道的摩阻压降、沿程摩阻以及摩阻系数代替管道管壁粗糙度进行研究。

3）流体性质

流体性质包括原油的黏度、密度等因素。在黏度方面，税碧垣等[6]人通过实验证明，当原油中加入同种类型且浓度相同的减阻剂时，随着原油粘度的降低，减阻率也会随着降低；在密度方面，目前还没有研究成果显示密度会对减阻率产生影响，但原油密度也是摩阻损失的影响因素之一，因此，有必要将密度暂定为减阻率影响因素之一。

4）流动参数

本次研究所讨论的流动参数包括原油的流速、温度、压力以及管道的高程。在流速方面，原油的流速不同，则管道内的流态产生一定的差异，目前的研究成果显示，如果原油处于层流状态，则减阻剂将无法发挥减阻效率，因此，流速也会对减阻率产生一定的影响[7-8]；在温度方面，当温度超过某一数值时，减阻剂的分子结构将会被破坏，当温度低于某一数值时，减阻剂分子将无法充分发挥自身作用，因此，温度也会对减阻率产生影响；原油所受压力会对其粘度和密度产生影响，沿程高程会使得原油的各种参数产生变动，因此，压力和管道高程可能会对减阻剂的减阻率产生影响[9]。由于原油的流速数据难以获取，因此，可以将原油的平均流速、平均输量、首站输量、末站输量代替流速数据进行下一步研究；原油温度可以使用管道首末站温度代替；管道沿程高程可以使用首末站高程代替。

5）雷诺数

目前已有研究表面，当雷诺数在[4 000，9 000]内变动时，随着雷诺数的增加，减阻剂的减阻率也会随之增大，但是当雷诺数超出该区间时，随着雷诺数的增加，减阻剂的减阻率会随着减小，因此，雷诺数也是影响减阻剂减阻率的重要因素。

根据以上分析，并将某些因素进行替换后，可以初选加剂浓度、管道管径、管道长度、摩阻压降、沿程摩阻、摩阻系数、油品黏度、油品密度、平均流速、平均输量、首站输量、末站输量、首站温度、末站温度、油品压力、首站高程、末站高程以及雷诺数等18 项数据作为减阻剂减阻率的影响因素进行下一步研究。

2 模型构建

2.1 PCA降维算法

通过上文分析可以发现，可能会引起减阻剂减阻率变化的因素较多，这为下一步的预测研究带来了一定的困难，因此，减少影响因素的数量十分必要，而PCA 算法正是减小影响因素数据的有效方法之一[10]。PCA 算法可以根据影响因素对减阻率影响的大小，从而将高维度数据转化为低维度数据，且在变化的过程中可以最大限度的保存数据的方差信息。该种算法简单可行，因此得到了大面积的推广和应用[11]。

PCA算法首先将初选的减阻率影响因素数据组合为矩阵X ，计算该矩阵的相关系数矩阵R，然后计算相关系数矩阵的特征值λi以及特征向量αi，相关系数矩阵R的计算公式如下所示：

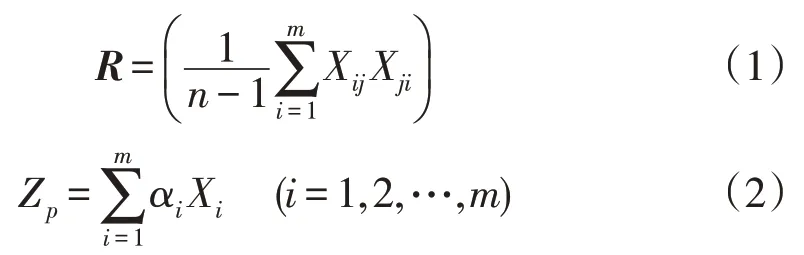
式中：Xij表示矩阵X 第i 行第j 列的数据；R 表示相关系数矩阵；αi表示相关系数矩阵的特征向量；Xi表示矩阵X 的第i 行数据；Zp表示计算得到的主成分。

2.2 GRNN神经网络算法

GRNN 算法是一种成熟的预测算法，该种算法由四层结构组成，分别是输入层、模式层、求和层以及输出层[12]。其基本结构如图1所示。

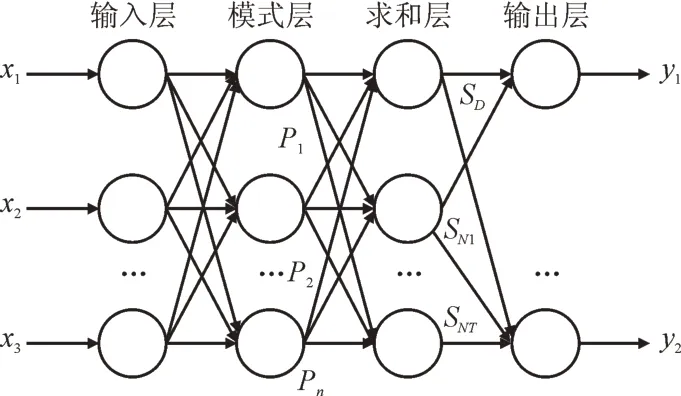
图1 GRNN模型网络结构

GRNN 算法基于非线性回归理论，首先假设求解变量x和变量y概率密度的函数为f(x,y)，如果变量x的观测值为X，此时，变量y相对于X的回归结果可以通过以下公式计算：

式中：Y就是待预测数据的预测结果。函数f(X,y)难以求处其准确值，只能通过估计的方式得到其结果，其估计公式为

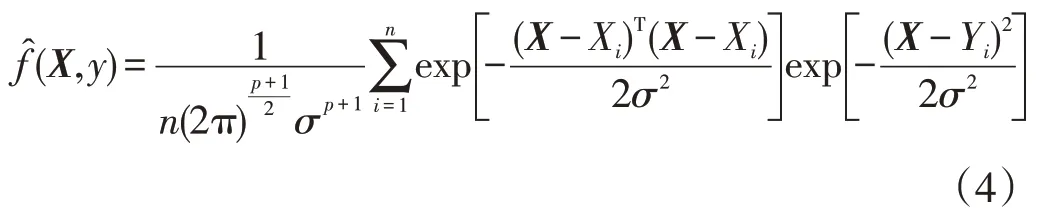
式中：Xi为变量x的观测值；Yi为变量y的观测值；n表示样本的数量；p为样本的维度；σ为光滑因子，当光滑因子的取值较大时，则预测结果将趋近于输入数据的平均值，当光滑因子取值较小时，预测效果相对较差[13]。因此，如何对光滑因子进行合理选择是一项难题，在本次研究中，使用交叉验证的方式对光滑因子进行优选。

2.3 模型组合

将PCA算法和GRNN 算法组合后的流程如图2所示。首先将18 种初选影响因素输入PCA 算法中，对其进行主成分分析，优选出累计贡献率高于98%的因素作为最终的减阻率影响因素。使用某公司生产的某种型号减阻剂，在我国某管道公司运营的管道上进行实验，最终得到155 组减阻剂减阻率实验数据，将135 组数据作为组合模型的训练数据，对剩余20组数据进行预测，并将预测结果与实际减阻率进行对比，计算每组数据的平均绝对误差，与Frank Vejahati、Karami所提出的方法、倒数方程法以及负指数方程法的计算结果进行误差对比。

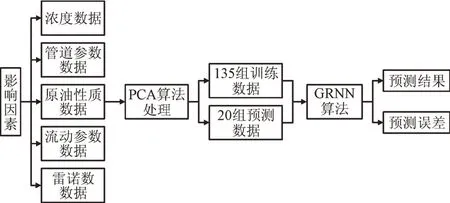
图2 PCA-GRNN模型预测流程

3 结果分析

3.1 降维结果分析

使用MATLAB 编程软件编写PCA 算法，将加剂浓度、管道管径、管道长度、摩阻压降、沿程摩阻、摩阻系数、油品黏度、油品密度、平均流速、平均输量、首站输量、末站输量、首站温度、末站温度、油品压力、首站高程、末站高程以及雷诺数等18 项数据输入PCA 算法中，对其进行主成分分析，分析结果如表1所示。从表1中可以看出，加剂浓度的贡献率高达44.988 6%，证明加剂浓度是影响减阻剂减阻率的主要因素。同时还可以看出，加剂浓度、管道直径、长度、平均输量、平均输送速度以及雷诺数六项影响因素的累计贡献率高达98%，因此，可以使用这六项影响因素代替所有初选影响因素进行GRNN预测。

3.2 预测结果分析

使用加剂浓度、管道直径、长度、平均输量、平均输送速度以及雷诺数六项因素作为减阻剂减阻率的影响因素，在MATLAB程序中建立GRNN模型，该模型的输入向量为7 维，输出向量为1 维，将135 组实验数据作为训练数据，对20 组数据进行预测，使用交叉验证的方式对光滑因子进行优选，优选结果为0.3。PCAGRNN 模型的预测结果如图3 所示，误差如图4 所示，PCA-SVM 模型、Frank Vejahati 所提出的方法、Karami所提出的方法、倒数方程法以及负指数方程法预测结果的平均绝对误差如表2所示。可以看出，PCA-GRNN模型的预测结果与实际减阻率十分接近，除第一组预测数据外，其他组别数据的预测结果均小于10%，第一组数据的误差小于25%，同时，该种模型的预测平均绝对误差为3.832%，远小于其他方法，证明使用人工智能程序预测减阻剂减阻率是可行的；Frank Vejahati 方法所考虑的影响因素数量较少，因此，预测平均绝对误差相对较大；Karami方法充分考虑了各种影响因素，预测平均绝对误差也相对较小；相对而言，负指数方程法和倒数法的预测误差相对较大，不推荐使用这两种方法。

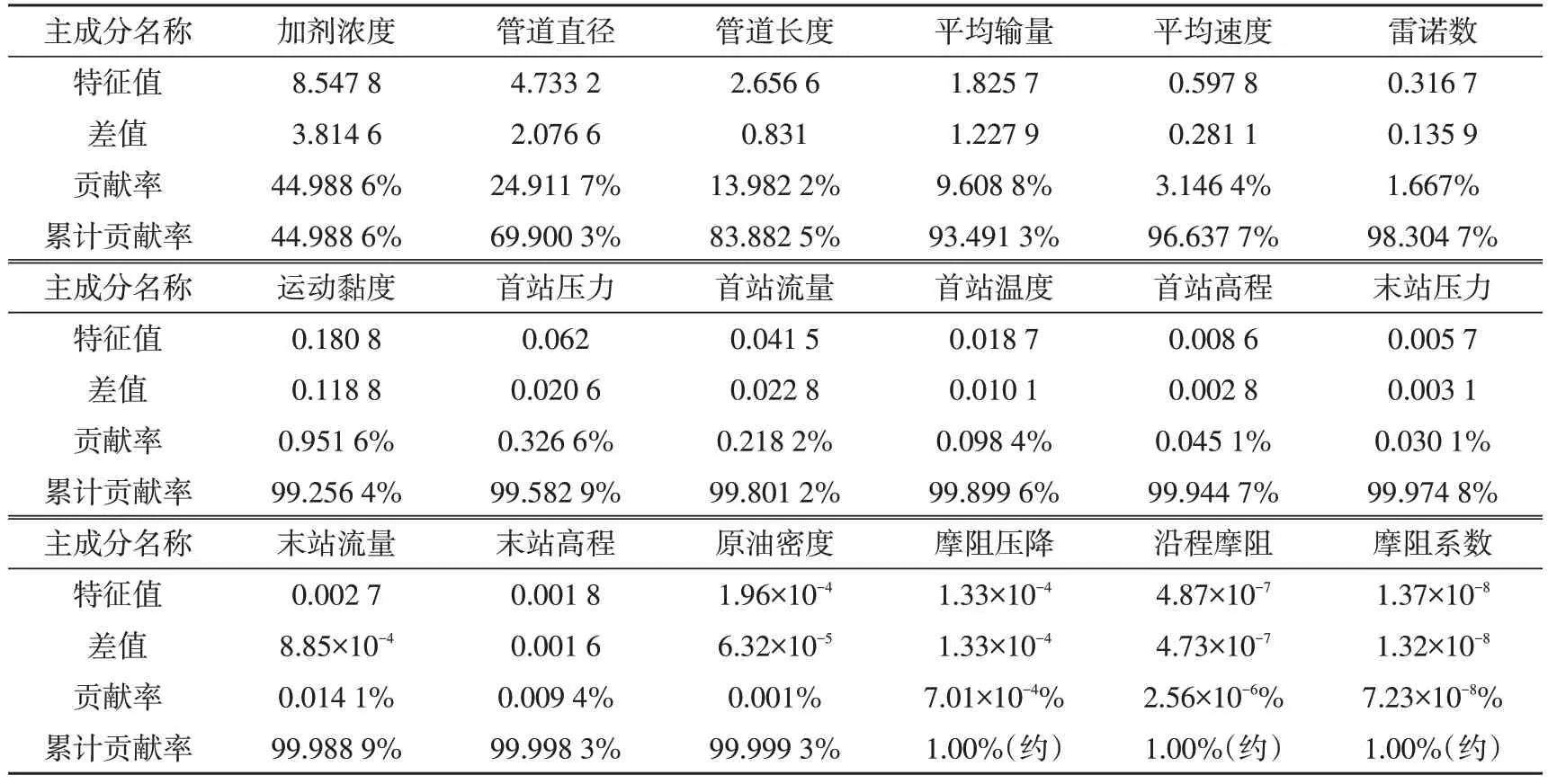
表1 主成分分析结果

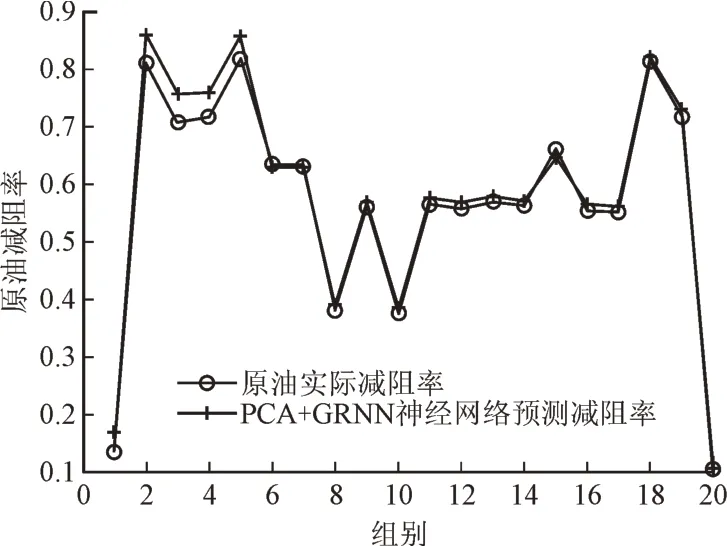
图3 PCA-GRNN模型的预测结果

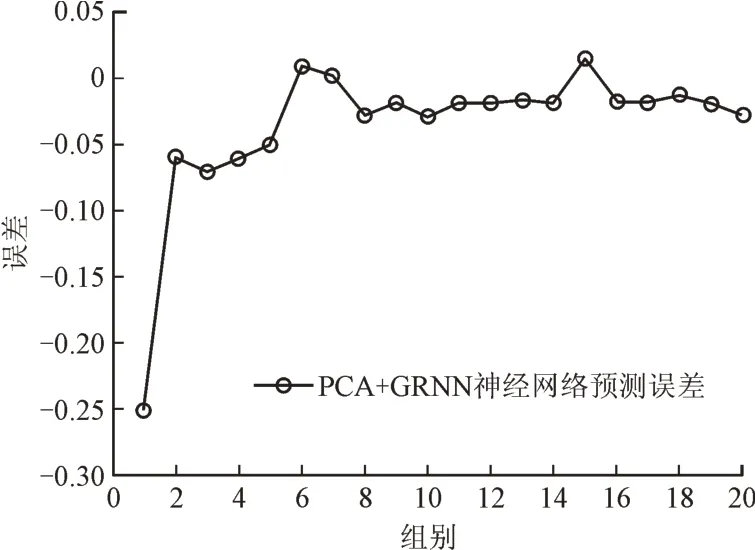
图4 PCA-GRNN模型的预测误差

表2 多种方法的平均绝对误差 %

4 结 论

在本次研究中，首先对影响原油减阻剂减阻率的相关因素进行了深入分析，初选出了18种可能引起减阻率变化的影响因素，使用PCA 算法对影响因素进行了降维处理，最后使用GRNN 算法对135 组数据进行了学习，对20 组数据进行了预测，并将预测误差与Frank Vejahati所提出的方法、Karami所提出的方法、倒数方程法以及负指数方程法的计算结果进行对比。通过此次研究，可以得出以下三条结论：

（1）加剂浓度、管道基本参数、流体性质、流动参数以及雷诺数都可能引起减阻剂减阻率产生变化，因此，减阻率的影响因素相对较多，传统的拟合公式难以准确的计算出减阻率数据；

（2）通过PCA降维结果可以看出，加剂浓度是影响减阻率最重要的因素，加剂浓度对减阻率的贡献率高达44.988 6%，同时，加剂浓度、管道直径、长度、平均输量、平均输送速度以及雷诺数六项影响因素的累计贡献率高达98%，因此，可以基于智能算法使用这六种因素对减阻率进行学习和预测；

（3）PCA-GRNN 模型的预测结果与实际减阻率十分接近，单组数据的预测误差最大不超过25%，平均绝对误差仅为3.832%，远低于其他方法，证明该模型完全可以用于减阻剂减阻率预测。