芯片原子钟磁屏蔽系统的设计与仿真

胡旭文，李云超，张 璐，牟仕浩，张开放，刘召军，张彦军，闫树斌

(中北大学 仪器与电子学院，山西 太原 030051)

0 引 言

芯片原子钟是基于原子在外加均匀弱磁场作用下发生塞曼分裂[1]，通过特定相干双色光的作用产生电磁诱导透明现象，实现高精度测量的计时工具，具有功耗低、体积小、成本低等优点[2-5].其结合微惯性测量单元组成Micro-PNT(Positioning Navigation and Timing，PNT)系统，与卫星导航技术相结合，可形成微型导航定位授时系统，构建PNT网络，具有完全自主、信息实时连续，且不受时间、地域限制等重要特性，被广泛应用于军事研究、科学试验和日常生活中[6-10].

原子气室作为芯片原子钟的核心部件，其在外加均匀弱磁场的激励下，碱金属原子能级打破简并，子能级发生塞曼分裂，基态的两个塞曼子能级与激发态能级之间发生(0，0)跃迁，从而产生CPT共振[11-12].外部杂散磁场(如地磁场)的存在会造成塞曼能级分裂的变化，引起碱金属原子的能级漂移以及谱线发生相应的频移，从而影响原子钟的跃迁信号和频率稳定度[13].由于外部磁场引起的频移量无法修正，故原子钟物理系统必须要屏蔽外部磁场对碱金属原子能级的扰动.因此，磁屏蔽装置对于原子钟来说是必不可少的.若要避免地磁场对原子钟原子能级的干扰，需要屏蔽装置将原子气室周围的剩余磁场减小到nT量级，即屏蔽系数不小于105.

目前，国内外对于磁屏蔽的研究主要侧重于屏蔽材料以及圆柱体磁屏蔽对屏蔽效能的影响，而对于球体磁屏蔽和圆柱体与球体嵌套磁屏蔽的研究相对较少.本文分析了屏蔽装置结构参数对圆柱体轴向屏蔽效能和球体屏蔽效能的影响，确定了最内层屏蔽体的相关参数.通过使用有限元软件Maxwell对4个嵌套模型进行仿真分析，综合考虑屏蔽效能和均匀度小于1%的区域，选定了屏蔽效果最佳的屏蔽模型，为后续芯片原子钟的性能测试提供低磁场环境.

1 理论分析

1.1 磁屏蔽原理

磁屏蔽原理可以采用图1 的结构来说明[14].高磁导率的屏蔽装置壁具有较小的磁阻，与其所围成空腔中的空气相比，更有利于磁力线通过，进入到空腔的磁通量也会相对较少，从而达到磁屏蔽的目的.

图1 磁屏蔽原理示意图Fig.1 Schematic diagram of magnetic shielding principle

1.2 多层磁屏蔽装置屏蔽系数

磁屏蔽系数S或屏蔽效能SE是衡量屏蔽装置性能的主要指标.磁屏蔽系数S是指磁屏蔽装置外部磁场Hout与内部磁场Hin的比值，即

(1)

屏蔽效能

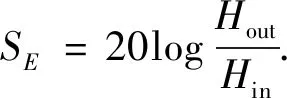
(2)

单层球体磁屏蔽的屏蔽系数[15-17]

(3)

式中：μr为相对磁导率；d为单层屏蔽的厚度；R为单层屏蔽截面内半径.单层圆柱体磁屏蔽的径向屏蔽系数

(4)

单层圆柱体磁屏蔽的轴向屏蔽系数可通过退磁因子N来表征

(5)

式中：P为轴径比，P=L/(2R).根据退磁因子公式可推导出N随着轴径比P的变化趋势，如图2 所示.由于圆柱体磁屏蔽的径向屏蔽系数较轴向屏蔽系数大很多，因此轴向屏蔽系数是制约屏蔽装置屏蔽效果的主要因素，本文对于圆柱体磁屏蔽将重点讨论其轴向屏蔽系数.

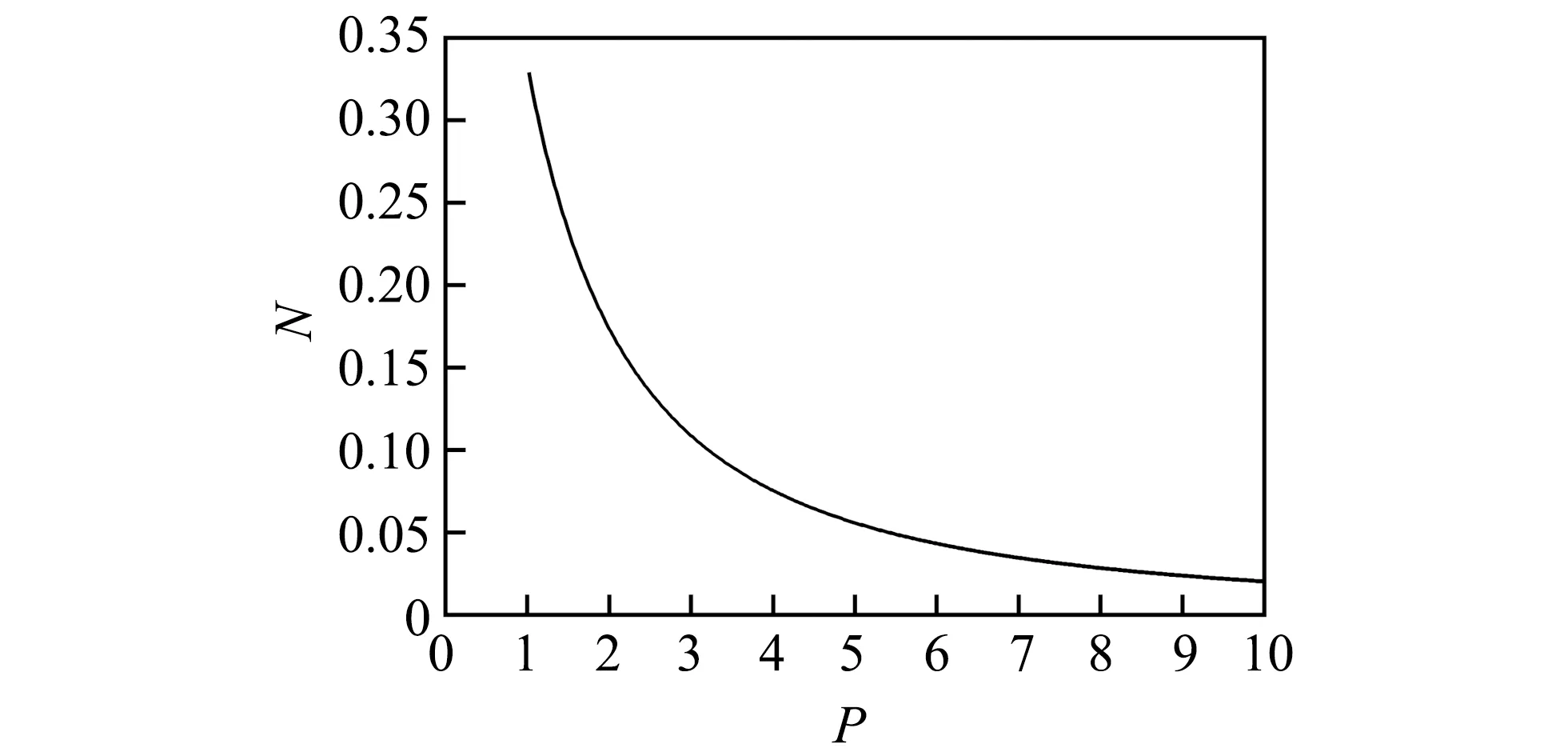
图2 N随P的变化曲线Fig.2 The curve of N with P

图3 为n层磁屏蔽筒的轴向剖面图，其中Ri和Li分别为第i层的平均半径和平均长度，ΔR和ΔL分别为层与层之间的径向间隔和轴向间隔.由单层屏蔽筒屏蔽系数可推导出n层磁屏蔽筒的轴向磁屏蔽系数[18]

(6)

式中：SAtot为总的轴向屏蔽系数；SAi为第i层磁屏蔽的轴向屏蔽系数.

图3 n层磁屏蔽筒轴向剖面图Fig.3 Axial profile of n-layer magnetic shield cylinder

同理，可以推导出n层球体磁屏蔽的屏蔽系数[19]

(7)

1.3 屏蔽材料的选择

软磁材料具有较小的矫顽力和较高的磁导率，可迅速响应外部磁场的变化，既容易被磁化，又容易退磁，是制作磁屏蔽的理想材料.常用的软磁材料相对磁导率如表1 所示.坡莫合金[20]具有较高的相对磁导率，其所含成分范围比较宽，其磁性能可通过改变成分含量和热处理工艺等方法进行调节，故选其作为磁屏蔽材料.

表1 常用软磁材料的相对磁导率Tab.1 Relative permeability of common soft magnetic materials

2 磁屏蔽装置参数设计及仿真

2.1 磁屏蔽装置参数设计

几何外形不同的磁屏蔽装置屏蔽效果也各不相同.为探究圆柱体磁屏蔽和球体磁屏蔽的屏蔽效果以及其屏蔽效能随着各结构参数(半径R，径向间距ΔR，长度L，轴向间距ΔL，厚度d)的变化情况，本文针对3层磁屏蔽装置，对式(6)和式(7)所包含的磁屏蔽装置设计所需的所有参数信息采用控制变量法，利用Matlab软件进行仿真，仿真结果如图4 所示，每个参数包含两条曲线，分别为圆柱体磁屏蔽轴向屏蔽效能SEA和球体屏蔽效能SE球.

图4 SE随各结构参数的变化曲线Fig.4 Variation curves of SE with various structural parameters

由图4 可知，3层球体磁屏蔽屏蔽效果要优于3层圆柱体磁屏蔽轴向屏蔽效果，这是因为相比圆柱体端盖，球体表面更有利于磁力线的通过.其中，球体磁屏蔽屏蔽效能随着径向间距ΔR和厚度d的增大而增大，且变化趋于平稳；随着半径R的增大而减小，且不随着长度L和轴向间距ΔL的变化而变化.圆柱体轴向屏蔽效能随着半径R和长度间隔ΔL的增大先增大后减小，存在极值；随着径向间距ΔR和厚度d的增大而增大，随着长度L的增大而减小.根据仿真结果和实际应用情况，考虑到屏蔽装置内要存放碱金属原子气室，亥姆霍兹线圈以及支架等结构，设定了最内层屏蔽装置尺寸，如表2 所示.

表2 屏蔽装置的最内层尺寸Tab.2 The innermost layer dimensions of shielding device

2.2 仿真与分析

通常地磁场的大小约为50 μT，其在3个方向上的分量为20 μT～30 μT.使用有限元软件Maxwell建立亥姆霍兹线圈模型模拟仿真某方向地磁场环境，在中心区域产生大小约为25.16 μT的近似均匀磁场，模型如图5 所示.图5(a)为亥姆霍兹线圈仿真模型；图5(b)为模型中心轴线上磁场的分布值；图5(c)为YZ平面磁场云图.

为进一步探究圆柱体磁屏蔽和球体磁屏蔽的屏蔽效果，以最内层结构尺寸为基础，设计4个3层磁屏蔽嵌套模型，如图6 所示.模型(1)为3层圆柱筒嵌套模型；模型(2)为1层球体和2层圆柱筒嵌套模型；模型(3)为2层球体和1层圆柱筒嵌套模型；模型(4)为3层球体嵌套模型.每个模型两端均有直径为6 mm的通光孔，圆柱筒模型一端固定，另一端有可拆卸的磁屏蔽盖.将4个模型分别放入地磁场模拟环境进行仿真，仿真结果如图7 所示.

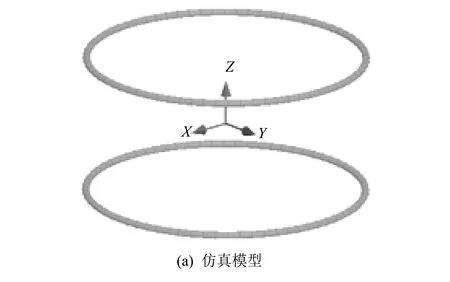
图5 亥姆霍兹线圈Fig.5 The helmholtz coil

图6 磁屏蔽嵌套模型Fig.6 Nested models of magnetic shielding

图7 轴向剩余磁场Fig.7 Axial residual magnetic field

仿真结果以屏蔽装置的中心为0点，沿着中心轴线向两侧采集数据.从结果可以看出，4个模型内部剩余磁场均小于10 pT，满足原子钟对内部剩余磁场的要求.3层球体磁屏蔽的屏蔽效果最佳，内部剩余磁场约为0.496 pT，而3层圆柱体磁屏蔽的屏蔽效果最差，内部剩余磁场为8.795 pT，这与之前讨论的结果一致，球体的屏蔽效果要好于圆柱体的轴向屏蔽效果.对各模型的理论计算结果和仿真结果进行对比，并计算各模型内部剩余磁场均匀度小于1%的范围，结果如表3 所示.由表3 可以发现仿真结果略小于理论计算结果，这是因为理论计算是在屏蔽装置完全密封的条件下进行计算的，而在仿真环境下，通光孔和屏蔽盖之间的缝隙对屏蔽装置的影响是不可忽略的，故而屏蔽效果会差一些.1层球体和2层圆柱体嵌套模型具有最大的磁场，均匀度小于1%的范围，约为22 mm；3层球体的范围最小，约为11 mm.综合考虑屏蔽效能和均匀区域，在内部剩余磁场满足条件的情况下，尽量选择均匀区域较大的屏蔽装置，故选择1层球体和2层圆柱体嵌套模型为磁屏蔽装置的最终设计模型.

表3 磁屏蔽装置的仿真结果Tab.3 Simulation results of magnetic shielding devices

3 结 论

本文从磁屏蔽原理出发，探究了圆柱体轴向磁屏蔽和球体磁屏蔽随着各结构参数的变化关系，得出球体屏蔽效果优于圆柱体轴向屏蔽效果的结论，并确定了最内层屏蔽装置的相关参数.使用Maxwell软件对4个圆柱体和球体的嵌套模型进行仿真并计算内部剩余磁场和均匀区域，选择2层球体和1层圆柱体嵌套模型作为最佳的屏蔽装置，屏蔽效能达到139.01 dB，均匀度小于1%的区域为22 mm.本研究对多层嵌套磁屏蔽装置的设计提供了一定的理论依据，对后续设计小尺寸结构磁屏蔽装置具有重要的指导意义.