组合双曲线法在高铁路基沉降预测中的应用
2019-07-18李华东
李华东
(中铁十六局集团第二工程有限公司 天津 300162)
1 引言
近年来中国在高铁建设上取得了举世瞩目的成就,从2008年我国第一条时速350 km京津城际开通运营,截至2018年我国高铁运营里程已达2.5万km。中国国家发展改革委指出“十三五”期间全国铁路营业里程达到15万km,其中高速铁路3万km,可以看出高速铁路建设仍是重中之重。高铁的高速性和舒适性依赖于线路的平顺性,而线下构筑物的变形量和稳定性是决定线路平顺的关键。大量工程实践[1-5]表明铁路路基沉降变形问题是造成铁路运行事故的主要原因,而通过沉降预测判断路基沉降是否趋于稳定从而确定最佳铺轨时间是在施工阶段保证高铁服役期安全运行的重要手段。
高速铁路桥涵、隧道、路基的沉降预测方法有指数曲线、双曲线、泊松模型、灰色理论、三点法[6-7]等。高铁路基施工过程主要包括填筑施工[8]和预压土堆载施工[9],在填筑完成进行堆载预压时,由于荷载施加较快易出现沉降速率突变,沉降曲线呈现较为明显的断层现象。目前,有些学者针对该问题进行了研究,杨涛等[10]针对软土地基分级填筑路堤的情况提出了多级双曲线沉降拟合方程,该方法可结合土力学中渗透固结理论对方程中参数进行理论上的解释,但对于高铁路基只存在一个断层的情况应用起来较为复杂且对于非软土地基缺乏普遍性。唐坤尧[11]引入邓肯-张模型采用数值计算的方法对软土路基沉降变形问题进行了分析,从理论上将沉降问题进行了较好的解释,但是未给出具体的预测方法且对沉降曲线断层问题没有涉及。有学者采用某些特定模型如基于VG模型的非饱和土沉降预测模型[12]、泊松曲线法[13]可以对“断层”不太明显的路基沉降曲线进行较好的拟合,但是对因堆载施工快速且路基本体填筑高度较小造成沉降曲线上出现明显“断层”的情况无法较好地进行拟合。
本文总结了常见高铁路基沉降预测方法的特点,针对堆载预压工况下路基沉降特点提出基于双曲线法的组合双曲线沉降预测模型,将该模型应用于京沈高铁路基段,将预测结果与其他常见沉降预测模型进行对比,验证了该模型具有较高的预测精度和适用性。
2 高速铁路路基常见沉降预测方法与组合双曲线法
2.1 常见沉降预测方法
目前,高速铁路路基沉降预测方法较多,如三点法、泊松曲线法、经验系数矫正法、指数曲线法、双曲线法等。下面对常见的沉降预测模型进行特点分析。
(1)三点法

式中,Sd为瞬时沉降(mm);S∞为最终沉降(mm);α、β为待求参数。
三点法也称对数配合法,在实测沉降曲线上任意选取三点:(t1,S1),(t2,S2),(t3,S3),且t2-t1=t3-t2,将选取的三点代入式中从而求得未知数Sd、S∞、β,其中Sd含有变量α,α可采用理论值或根据实测资料计算得到。以下为求解过程:
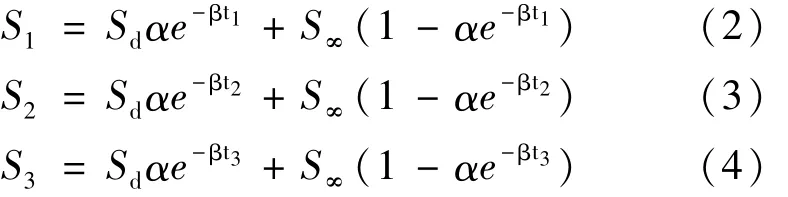
由此解得:
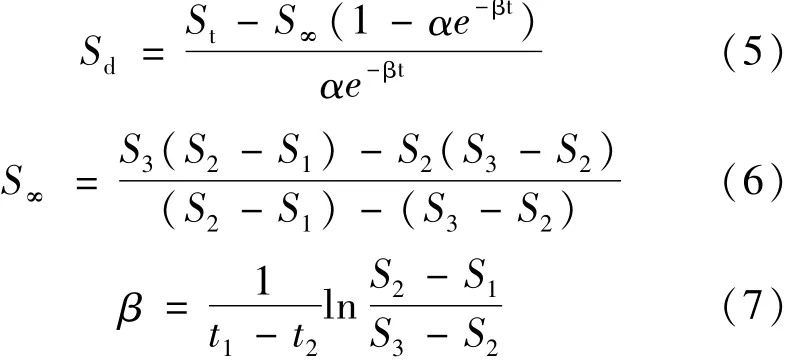
(2)泊松曲线法

式中,a、b、k均为待求参数。
泊松曲线又称为生长型曲线,反映了事物产生、发展、成熟最后达到极限的过程。这与荷载逐渐增加沉降量逐渐变大最后是否趋于收敛相类似。其求解方法可采用实测沉降数据求出3个参数从而得到任意时刻的沉降量。泊松曲线的特点是不过原点,曲线形状为“S”形,可对软土地基沉降曲线进行较好的拟合,对由于预压在曲线上产生的较大“断层”沉降曲线的预测有待进一步验证。
(3)指数曲线法与双曲线法
指数曲线法与双曲线法都属于曲线拟合法,采用与实际沉降曲线相类似的曲线进行曲线拟合,相关系数达到一定程度后对时间序列进行外延从而求出后期沉降量。该方法属于经验方法,在沉降曲线与所选曲线形状相似程度较高时常得到比较准确的预测结果,且预测方法简单明了具有一定的实用性,但目前常用的曲线(如沉降时间倒数法、指数曲线、双曲线等)较难与实测沉降曲线中产生的较大“断层”相类似。
(4)经验系数矫正法

式中,Sc为主固结沉降;m为经验系数,其与加载速率、地基处理方式、地基类型有关,当有合理的参考资料时所作的预测相对准确,无法进行没有基于经验和资料的工程进行预测。
经验系数矫正法应用较为简单,但是预测结果很大程度上取决于经验系数的选取,具有一定的局限性。
2.2 组合双曲线法
《客运专线铁路无砟轨道铺设条件评估技术指南》中指出双曲线法具有参数少、操作简单的优点,因此将双曲线法作为首选评估方法,但是传统双曲线法无法较好地对沉降曲线中的“断层”进行拟合,因此将双曲线法进行组合改进,具体组合方法如下。
实测沉降曲线表明在路基完成填筑,堆载预压施工开始时高铁路基沉降曲线常出现“断层”。因此,将沉降过程分为2个阶段:填筑期和堆载预压期。2个阶段的分界点为堆载预压时刻td,因此沉降拟合方程也由两部分组成。
填筑期模型公式为:
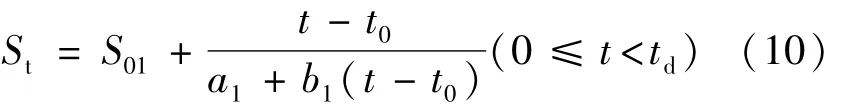
式中,St为t时刻的沉降量(mm);S01为填筑期时间起点沉降量;t0为填筑期时间起点;a1、b1为待定参数。
预压期模型公式为:
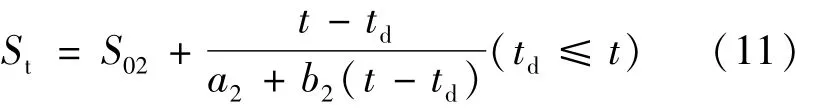
式中,St为t时刻的沉降量(mm);S02为预压期时间起点沉降量;S02与填筑完成时沉降量一致;td为填筑期与堆载预压期的临界时间;a2,b2为待定参数。
以预压期模型为例对未知参数进行求解。将式(11)改写为:
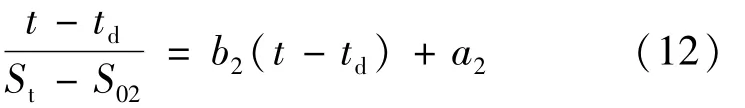
可以看出a2、b2分别为(t-td)/(St-S02)-(t-td)线形关系的截距与斜率,可代入实测沉降量St与时间t序列采用最小二乘法求出参数a2、b2,再代入时间求出某个时刻的沉降量和函数的极限值即最终沉降量。令x=t-td,y=(t-td)/(St-S02),则有:

根据最小二乘法原理,可以解得:
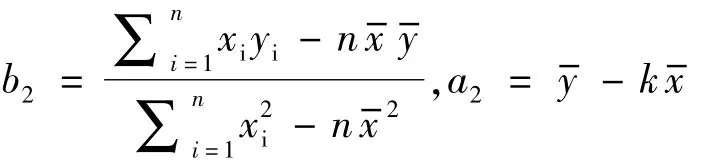
三点法要求所取三点为等时距选取,而现场沉降观测受天气、施工等影响,所测数据常出现不同间隔,在评估预测之前还需等时距处理,因此该过程较为复杂。选择不同的三点所得预测结果常常出现较大的差距,这为确定最终沉降带来较大不便。泊松曲线法是适用于软土地基具有较高预测精度的预测方法,但要求数据等时空间距。指数曲线法和双曲线法是较为常用的沉降预测方法,具有方法简单参数较少的优点,但由于沉降曲线中断层的存在无法较好拟合。经验系数矫正法在有成熟的经验时预测较为准确,但是预测结果很大程度上取决于经验系数的选取,具有一定的局限性。基于以上原因提出基于双曲线法的组合双曲线沉降预测模型从而达到模型简单实用且与实测沉降曲线具有较高拟合程度的效果。
3 组合双曲线法在京沈高铁路基沉降预测中的应用
京沈高铁设计时速350 km,起于北京途经河北承德、辽宁朝阳、阜新最终会于沈阳站,线路全长709 km,全线路基长度170 km。沿线分布有农田、河流、村庄、鱼塘、荷塘及公路等。挑选原地面为池塘的不良地质段DK480+013.92~DK481+409.50为试验段,路基最大填筑高度10 m,基底下部自上而下分别为新黄土、细圆砾土、粗圆砾土等。地下水位埋深8.4~24.0 m,不具侵蚀性。地震动峰值加速度为0.05 g。路基基底采用灰土挤密桩+CFG桩加固,正方形布置。为了保证高铁路基段线路的平顺性、有效控制填筑质量、在保证工程安全的同时准确合理确定预压土的卸除时间,须对该工程典型的路基段进行施工期和工后沉降观测以及后期沉降预测。由于篇幅限制对具有代表性的断面DK481+195、DK481+245、DK481+295中心地基顶面沉降板进行沉降分析。
图1为时间-沉降-填土曲线,可以看出填筑期由于荷载的逐步施加沉降量和沉降速率均较大,随着路基本体的填筑完成沉降量和沉降速率迅速变小;预压土堆载后出现较大的沉降,堆载预压后期逐渐趋于平缓,可以看出填筑期和预压期曲线形状都类似于双曲线形式,因此采用组合双曲线法对其进行沉降预测。
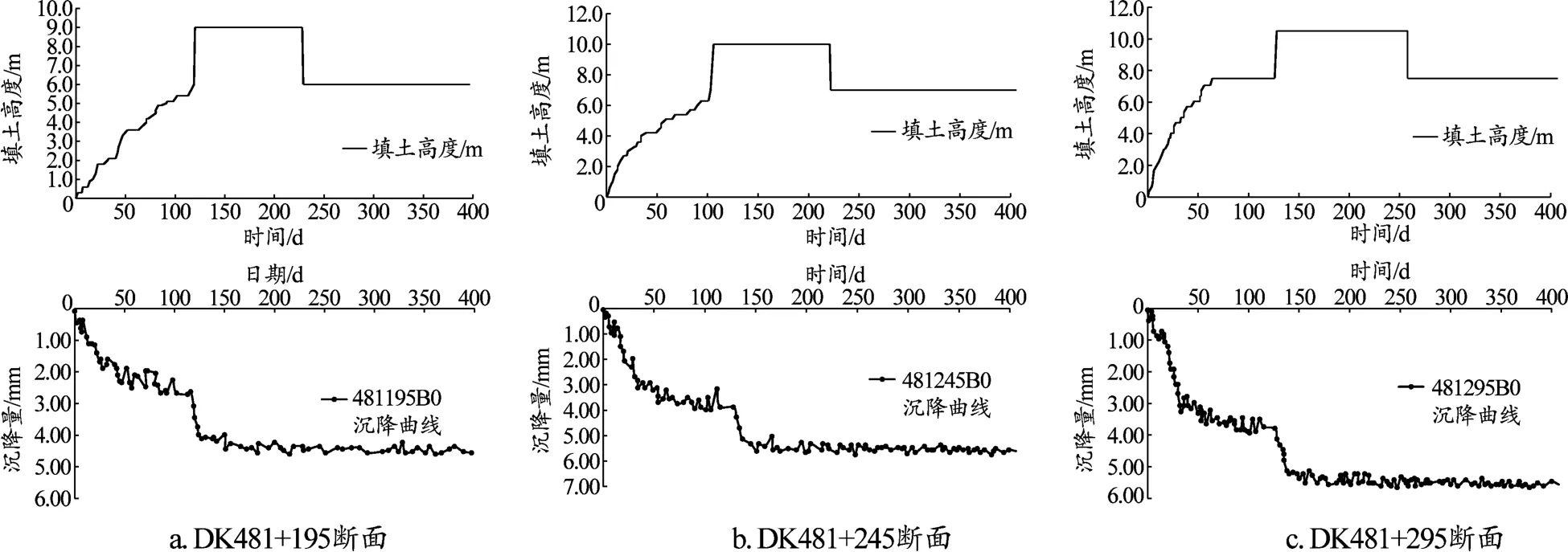
图1 时间-沉降-填土曲线
采用组合双曲线法进行曲线拟合所得计算结果见表1,可以看出采用组合双曲线计算的相关系数很高,分别为 0.96、0.97、0.98。
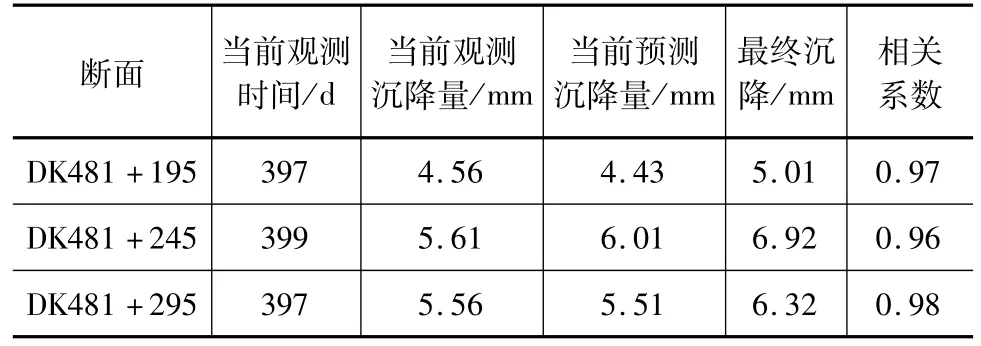
表1_组合双曲线_法沉降计算结果统计
为了证明组合双曲线法由于堆载预压产生带有“断层”沉降曲线的适应性,分别对比了双曲线法、指数曲线法、三点法的拟合结果,其沉降拟合图见图2。可以看出传统的双曲线法、指数曲线法和三点法在填筑初期和预压土卸除后期可以较好的拟合,但是对于td时刻之前大约40 d,之后大约60 d的数据均无法较好的拟合;组合双曲线法计算所得相关系数较高而双曲线法、指数曲线法和三点法相关系数普遍较低。因此,组合双曲线法相较于文中其他沉降预测方法预测精度较高。
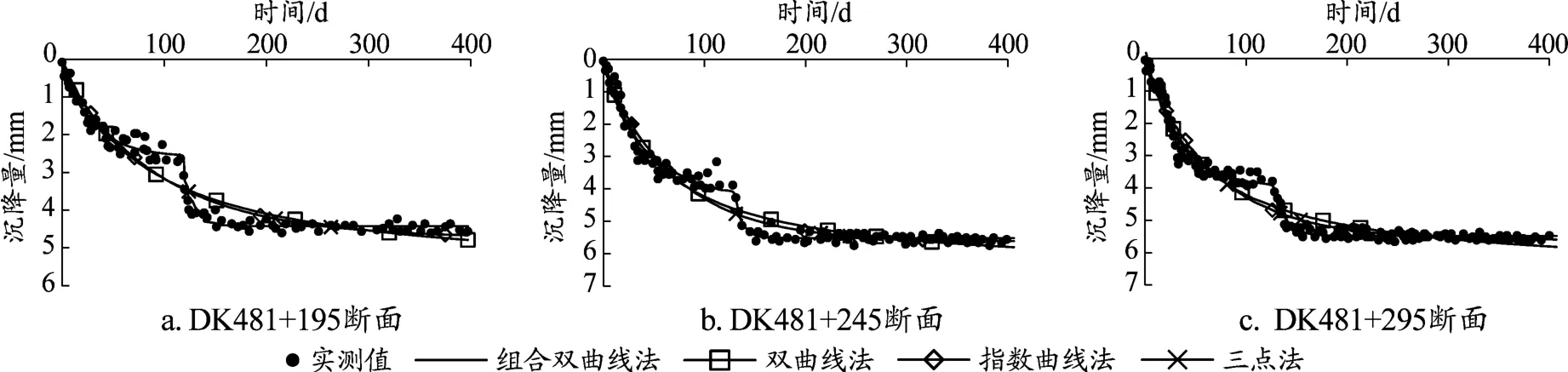
图2 不同预测模型沉降预测结果
4 结论
(1)综合分析三点法、指数曲线法、双曲线法模型特点,表明对于带有明显“断层”的沉降曲线该类方法不具有适用性。
(2)给出了组合双曲线法的求解过程,采用分段进行参数拟合的方法可以解决沉降曲线出现“断层”的现象。
(3)将不同沉降预测方法应用于京沈高铁路基工程,组合双曲线法相对于其他沉降预测方法具有较高的相关系数,且可以较好地对存在“断层”的沉降曲线进行拟合。
[4] 中国铁道科学研究院.高速铁路无砟轨道线路维修规则(试行):TG/GW 115-2012[S].北京:中国铁道出版社,2012:95-96.
[5] 刘钰.CRTSII型板式轨道早期温度场特征及其影响研究[D].成都:西南交通大学,2013:42-48.
[6] 车晓娟.轨道板配筋对温度裂缝的影响分析[D].成都:西南交通大学,2007:34-35.
[7] 林波.混凝土收缩徐变及其效应的计算分析和试验研究[D].南京:东南大学,2006:7-9.
[8] 邵永健,翁晓红,劳裕华.混凝土结构设计原理[M].北京:北京大学出版社,2015:13-15.
[9] 王玉镯.ABAQUS结构工程分析及实例讲解[M].北京:中国建筑工业出版社,2010:31-33.
[10]曹金凤,石亦平.ABAQUS有限元分析常见问题解答[M].北京:机械工业出版社,2009:88-92.
[11]赵坪锐.客运专线无砟轨道设计理论与方法研究[D].成都:西南交通大学,2008:71-72.
[12]铁道第三勘察设计院集团有限公司,中铁第四勘察设计院集团有限公司.高速铁路设计规范:TB 10621-2014[S].北京:中国铁道出版社,2015:88-89.
[13]铁道第三勘察设计院集团有限公司.铁路桥涵设计基本规范:TB 10002.1-2005[S].北京:中国铁道出版社,2005:56-57.
[14]中铁一局集团有限公司.高速铁路轨道工程施工技术指南:铁建设〔2010〕241号[S].北京:中国铁道出版社,2011:34-35.
