三维摄影测量技术在土工离心模型试验中的应用
2019-07-18贾程宏侯瑜京魏迎奇张雪东张紫涛梁建辉
贾程宏,侯瑜京,魏迎奇,张雪东,张紫涛,梁建辉
(中国水利水电科学研究院 岩土工程研究所,北京 100048)
1 研究背景
土工离心模型试验是将模型置于特定的离心机中,使1/n缩尺的模型在ng离心加速度的空间进行试验。由于惯性力与重力绝对等效,且高加速度不会改变工程材料的性质,从而使模型与原型的应力应变相等、变形相似、破坏机理相同,能再现原形特性[1]。土工离心模型试验技术的发明大大推动了岩土工程的学科进步,目前土工离心模型试验技术被应用于岩土工程领域的诸多方面,侯瑜京等[2]在离心机中研究了垃圾土边坡的失稳特性;魏迎奇等[3]基于LXL-4-450离心试验平台,对新型机载设备及相应的试验成果进行了总结。张雪东等[4]通过土工离心模型试验研究了水下爆破对大坝的影响。近年来岩土力学的发展对土工离心模型试验的设计提出了更高的要求。在土工离心模型试验中,模型的变形监测是很重要的一部分,传统的测量手段有:(1)差动变压器式位移传感器。它是线性可变差动变压器(英文简称:LVDT)的一种,属于接触式传感器。工作原理简单地说是铁芯可动变压器,在离心模型试验中,需要严格控制LVDT与模型表面的接触,以保证测得数据的准确性,这必然会对模型的物理性能产生一定的影响,且传感器的量程和布设个数限制了位移的测量范围和数量[5]。再加上高重力场的影响,使得它不能在试验过程中及时跟踪被测表面的沉降,抗干扰能力较差。(2)激光传感器。离心模型试验中的激光传感器采用高分辨率CMOS线性阵列和DSP技术工作并借助测量角度确定距离,它的测量精度高,抗干扰能力强,但是它的光强会受到多种因素的影响,且只能测量事先布置好的有限个点的数据。不同于以上两种测量手段,摄影测量技术通过电子摄像设备获取模型在加载过程中的图像,从而获得模型表面任意时刻的位移场[6-7]。
因为摄影测量技术具有非接触、直观、测量范围广等优点,许多土工离心机技术研究人员提出了研制摄影系统的要求。摄影测量技术的基本原理是通过分析模型图像中关键点的位置变化,计算模型对应位置的位移量。这种基于数字图像的位移测量技术因其无需人为标点等优点已在土工试验、离心模型试验以及现场试验中得到了一些应用[8-9]。清华大学张嘎教授团队应用摄影测量技术对土坡的变形发展直至破坏的全过程进行了测量[10]。应用摄影测量技术可以根据具体要求,计算模型表面各点在任意方向上的位移,从而分析出模型在任意方向上的变形。中国科学院武汉岩土力学研究所的任伟中教授等应用数码像机数字化近景摄影测量技术对采矿过程中地表及上、下盘岩体中的位移进行了量测[11]。以上研究主要是对模型表面各点平面位移的测量以及对非离心状态下模型三维变形的测量。基于这些研究成果,本文提出了三维摄影测量技术,该技术应用两台摄像机实现了对土工离心模型变形的三维测量,并且扩大了测量的范围。
2 三维摄影测量技术原理
刘怀忠等从摄像设备成像的透视原理出发,对物-像坐标的对应关系进行推导,获取像坐标到物坐标的表达式[8]。这种方法通过模型箱坐标系、摄像机视点坐标系、物像坐标系、像素坐标系4个空间坐标系建立物-像坐标之间的关系,由已知坐标的参考点对各坐标系之间的转换参数以及摄像机的内置参数进行标定。参照这种方法,本文建立了可以应用于土工离心模型试验变形监测的三维摄影测量技术。
在土工离心模型试验中,摄像机采用的是CCD(Charge-coupled Device)成像技术,因此建立世界坐标系、相机坐标系(光心坐标系)、图像坐标系和像素坐标系4个坐标系,摄影流程如图1所示,4个坐标系之间的关系如图2所示,其中,M为三维空间点,m为M在图像平面投影成的像点。世界坐标系是客观三维世界的绝对坐标系,在土工离心模型试验中,世界坐标系即为模型箱坐标系,X轴、Y轴和Z轴分别沿模型箱的长边、宽边以及高边建立,不随模型箱的转动而改变。在此坐标系中,用(Xw,Yw,Zw)表示各点的坐标值。相机坐标系以相机的光心为坐标原点,X轴和Y轴分别平行于图像坐标系的X轴和Y轴,相机的光轴为Z轴,用(Xc,Yc,Zc)表示此坐标系中各点的坐标值。图像坐标系以CCD图像平面的中心为坐标原点,X轴和Y轴分别平行于图像平面的两条垂直边,用(x,y)表示此坐标系中各点的坐标值,用物理单位(例如毫米)表示像素在图像中的位置。像素坐标系以CCD图像平面的某一个顶点为原点,X轴和Y轴分别平行于图像坐标系的X轴和Y轴,用(u,v)表示此坐标系中各点的坐标值。

图1 摄影流程图
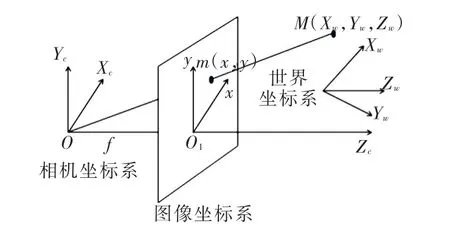
图2 四个坐标系的关系图
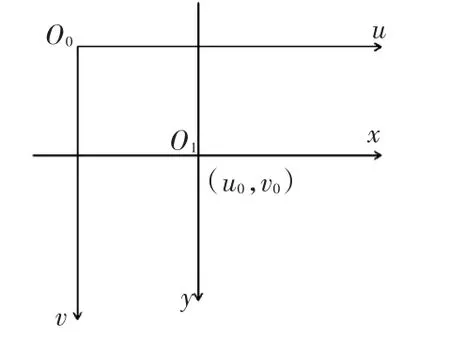
图3 图像坐标系与像素坐标系的关系
数码相机采集的图像首先形成标准电信号的形式,然后再通过模数转换为数字图像。每幅图像的存储形式是M×N的数组,M行N列的图像中每一个元素的数值代表的是图像点的灰度。这样的每个元素叫像素,像素坐标系就是以像素为单位的图像坐标系。像素坐标系与图像坐标系的关系如图3所示。利用齐次坐标可将它们之间的关系表示为矩阵形式:

其中(u0,v0)是图像坐标系原点在像素坐标系中的坐标,dx和dy分别是每个像素在图像平面X轴和Y轴方向上的物理尺寸,且大小相等。图像坐标系与相机坐标系的转换关系式为:

其中f为焦距,也就是像平面与相机坐标系原点的距离。可用齐次坐标阵将上述关系表示为矩阵形式:

相机坐标系与世界坐标系的转换关系式为:

其中,R为3×3正交旋转矩阵,t为三维平移向量,综合起来可得像素坐标与世界坐标之间的转换关系,用矩阵形式可表示为:

在上述转换式(6)中,共含有7个参数,分别是三维状态下相机的3个位置参数,构成三维平移向量t,3个角度参数,构成正交旋转矩阵R,以及由相机焦距和像素在图像坐标轴上的物理尺寸决定的无量纲参数a。根据式(6),可由已知像素坐标和世界坐标的标记点标定出摄像机的这7个参数。若已知一点的像素坐标(u,v),则式(6)中含有Zc、Xw、Yw、Zw共4个未知量,故无法求解。若使用两台摄像机拍摄到的结果,方程可以增加3个,未知量只增加了1个Zc,这时就有6个方程,只包含5个未知量,可以进行求解。
3 三维摄影测量技术在土工离心模型试验中的应用
3.1 试验简介在对三维摄影测量技术的原理进行探究后,本文将该技术应用于具体的土工离心模型试验中进行了计算与验证。离心模型试验的原型是西南某软土地基土石坝,软土地基的含水量高,天然空隙相对较大,具有较高的压缩性[12-14]。由于软土地基工程性质较差,施工期和工后期地基土的持续沉降、变形会造成其上的构筑物损坏、失稳[15]。
土石坝模型坝体土料的基本参数如表1所示,坝基淤泥土的基本参数如表2所示。
试验布置如图4所示,软土坝基模型长1.28 m,宽0.715 m,土石坝模型高0.12 m,坡比为1∶2.7。试验前在土石坝模型表面用石灰及颜料绘制了50个标记点,试验过程中用这些标记点表示坝基及土石坝的位移状态。为了尽可能的拍摄到所有的标记点,且能够计算出它们的实时三维坐标,将两台型号为208C的摄像机1号、2号对称地架设于模型箱的顶部两端,其拍摄效果如图5所示(试验前)。

表1 坝体土料基本参数

表2 坝基土料基本参数
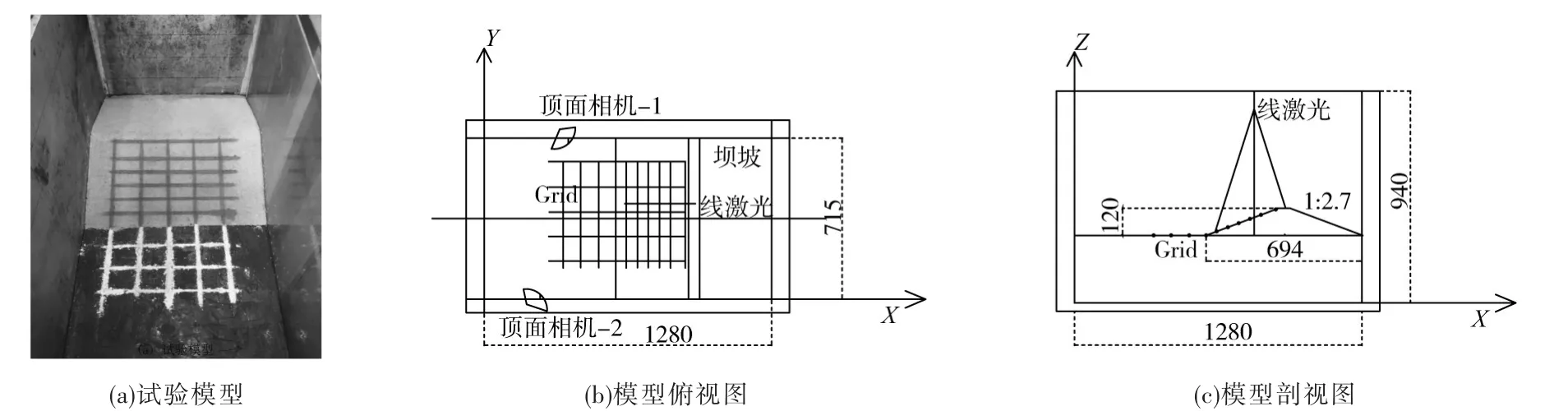
图4 试验布置图

图5 两台摄像机拍摄效果
离心模型试验过程如图6所示。离心模型试验共分为5个阶段,试验过程全部被两台摄像机记录下来,试验后模型效果如图7所示。由图7可以看出,离心模型试验后土石坝模型发生了明显的沉降,尤其是坝顶,这种沉降沿着坝坡面逐渐减小,坝底及与坝坡相交处的坝基甚至有向上拱起的趋势。为了描述土石坝模型在离心模型试验过程中的变形,从录像中选取了离心加速度分别为0g(试验前)、20g、40g、60g时对应的图像。由于离心加速度为40g和60g时,有较长时间的稳定期,故各选取了3张图像,分别是40g稳定期开始、运行145 s、结束时以及60g稳定期开始、运行90 s、结束时对应的图像。
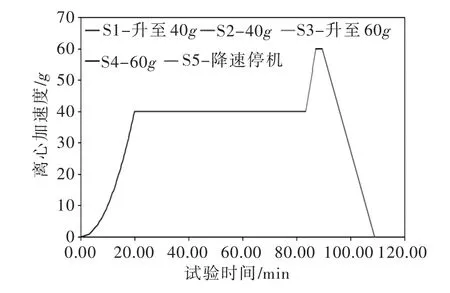
图6 试验过程图

图7 试验后模型效果
3.2 参数标定所有选取图像的像素大小相同,宽度方向上的像素大小为352,高度方向上的像素大小为288,选取离心加速度为0g时的图像,找到各个标记点在图像中的像素坐标。确定各个标记点像素坐标的具体操作方法是先找到每个标记点四个角点的坐标,再计算出其形心坐标作为该点的像素坐标。以模型箱的长边、宽边以及高边为世界坐标系的X轴、Y轴、Z轴,计算出初始时各个标记点的世界坐标。在已知这些标记点的像素坐标和世界坐标的前提下,通过Matlab程序分别迭代计算出1号摄像机和2号摄像机的参数。经过计算,得到1号、2号摄像机的参数如表3所示。

表3 摄像机1号、2号的参数
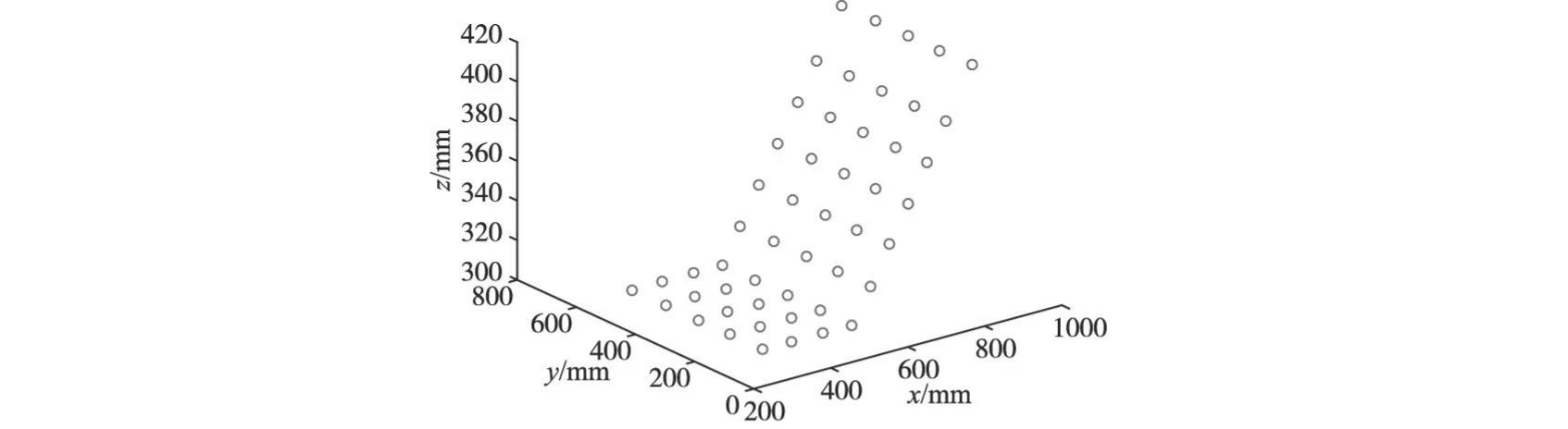
图8 离心加速度为0g时各个标记点的理想世界坐标
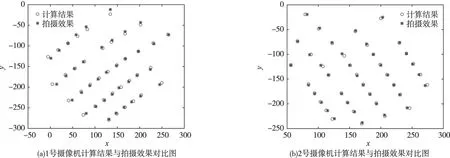
图9 两台摄像机计算结果与拍摄效果对比图
利用求得的相机参数,由离心加速度为0g时各个标记点的理想世界坐标计算出其像素坐标。之所以称为理想世界坐标,是因为试验过程中,各个标记点实际的世界坐标因模型制作不平整,必然会与理想中的世界坐标有所出入。将计算得到的像素坐标与1号、2号摄像机拍摄到的结果进行对比,如图8~9所示。图8采用世界坐标系,即模型箱坐标系,图9采用像素坐标系,像素单位为1。
经过计算,标记点的像素坐标在由计算得到的结果与由图像得到的结果之间,图9(a)中,像素坐标系X轴上的平均偏差是0.06个像素坐标,Y轴上的平均偏差是0.07个像素坐标;图9(b)中,像素坐标系X轴上的平均偏差是0.01个像素坐标,Y轴上的平均偏差是0.02个像素坐标。综上,两个方向上像素坐标的平均偏差相对于该方向上像素大小的比均小于0.3%,引起偏差的主要原因是模型表面并非理想平面。计算结果说明相机参数合理有效,可以用于计算分析模型的变形过程。
3.3 变形计算由离心机加速度为0g时两台摄像机拍摄到的图像,计算出此时各个标记点的世界坐标。需要说明的是,在同一时刻,摄像机1号与2号拍摄到的标记点可能不同,为有效计算,这里只统计计算两台摄像机共同拍摄到的标记点。将计算结果同模型的理想世界坐标进行对比,如图10所示。
测得所有标记点的世界坐标同其理想世界坐标的平均偏差,在模型箱长度方向上为0.08 mm(绝对值,下同),在模型箱宽度方向上为0.30 mm,在模型箱高度方向上为0.35 mm。相比于模型尺寸,三个方向上的偏差比均小于1%,且偏差在三个方向上的标准差分别为5.50 mm、5.69 mm、5.41 mm,有一定的波动,但波动幅度接近,主要原因是模型表面非理想平面,个别标记点的实际世界坐标与理想值偏差较大,但这些偏差并不会影响对于模型整体变形的判断。在本试验中,我们主要关注模型的沉降变形,即各个标记点的z值变化,故下文中提到的各坐标数值默认为z值。
接下来,选取两台摄像机拍摄到离心加速度分别是20g、40g、60g时的模型图像,其中,20g时1张,40g、60g时各3张,计算统计出每张图像上各个标记点的像素坐标。利用这些像素坐标,通过Matlab程序计算出对应离心加速度时各个标记点的世界坐标,并与离心加速度为0g时(初始状态)计算出的各个标记点的世界坐标进行对比,如图11所示。

图10 0g时各个标记点的世界坐标同其理想值的对比
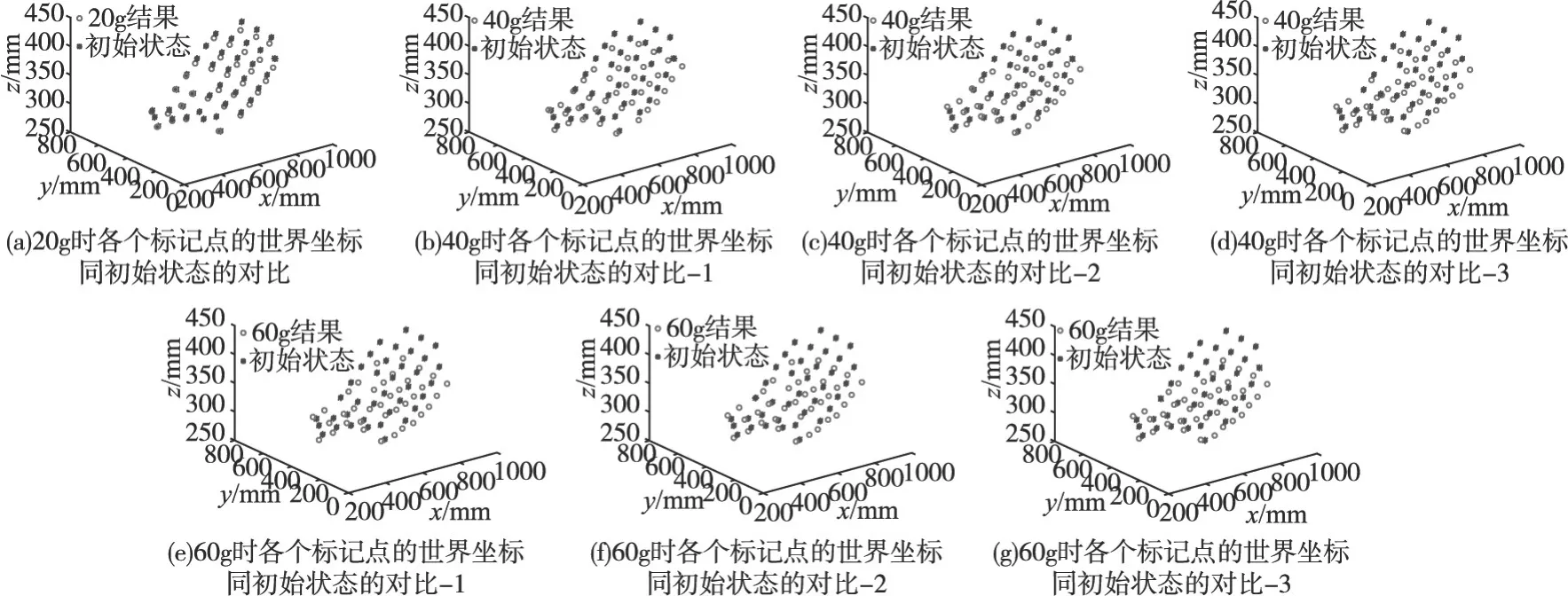
图11 不同状态下各个标记点的世界坐标同初始状态的对比
计算结果表明,在离心模型试验过程中,随着离心加速度的增大,坝体逐渐下沉,且坝顶沉降最明显,坝顶中部沉降超过50 mm,两侧沉降略小于50 mm,可能与模型箱侧壁的摩擦限制沉降有关。最大沉降变形超过坝体高度的40%,最终发生了变形破坏。离心试验结束时的坝顶沉降如图12所示,靠近坝顶的4个标记点的平均沉降量为50.99 mm,沉降量标准差为1.00 mm。
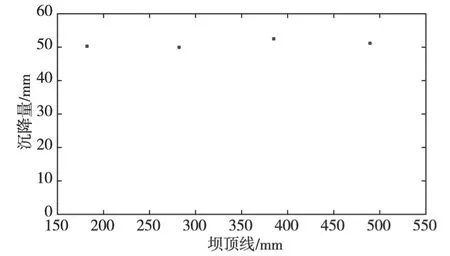
图12 沿坝顶线的最终沉降量

图13 沿坝坡与坝基相交线附近的最终沉降量
坝坡表面沉降量沿着坝坡向下逐渐减小,在接近与坝基相交处,沉降量变得很小,局部出现向上拱起的现象。由于坝坡与坝基相交处已知标记点较少,因此以接近相交线的一组坝坡上标记点为研究对象。这一区域的沉降量均小于10 mm,如图13所示。已知4个标记点的平均沉降量为5.74 mm,沉降量标准差为2.02 mm。
随着距离坝坡与坝基相交处越来越远,坝基的沉降也越来越明显,但本次试验所测范围有限,可测范围内沉降量均小于10 mm。为研究土石坝模型在整个试验过程中的变形,取最具代表性、数据最全的模型中轴线上的一系列数据进行研究,如图14所示。

图14 试验过程中土石坝模型中轴线上的变形
图中实线是根据试验开始前各个标记点位置拟合而成的,可以看出,前文所陈述的结果在此图中也有所反映。离心模型试验过程中,坝顶沉降最大,且沉降量沿着坝坡向下逐渐减小,在坝坡与坝基相交处,沉降量很小,局部区域出现向上拱起的现象,远离坝体的坝基也发生了明显的沉降。由图14还可以看出,在下沉过程中,坝体逐渐向坝基一侧移动。
3.4 对照分析在试验过程中,模型箱顶部用金属架固定了一台激光传感器。激光传感器是型号为CP08MHT80的高精度测距传感器,直线性为0.1%,具有8 μm的高分辨率。
由于激光传感器测量范围是模型中轴线附近的坝坡,所以可将激光传感器测得对应时间的坝坡沉降变形过程与前文结果进行对照。由激光传感器测得土石坝模型中轴线附近坝坡的沉降变形如图15所示。
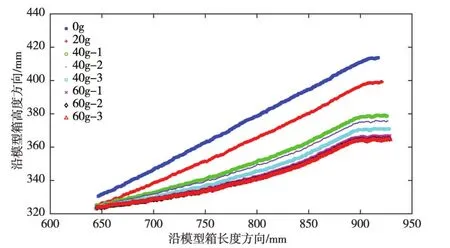
图15 试验过程中土石坝模型中轴线附近坝坡的沉降变形
由图15可以看出,在离心模型试验过程中,模型中轴线附近坝坡的沉降随着离心加速度的增大而增大。数据表明,最终坝顶沉降为49.11 mm,且沉降量沿着坝坡向下逐渐减小,在与坝基的相交线处,沉降量小于10 mm,变形不明显。对照图14,由激光传感器和三维摄影测量技术测得的模型沉降变形过程一致,说明三维摄影测量技术可用于对该离心模型进行变形监测。
试验中由激光传感器测量的区域与三维摄影测量的标记点不重合,选取激光传感器测量区域周围的3组标记点,求取各组标记点试验结束时(60g-3)沿模型箱高度方向上的坐标平均值,并将它们与由激光传感器测量得到的结果进行对比,如图16所示。数据表明,由三维摄影测量技术与激光传感器测得数据的最大偏差是8.89 mm,占土石坝模型高度的7.4%,平均偏差是0.56 mm,占土石坝模型高度的0.5%。造成偏差的主要原因是两种方法测量的点不重合,模型表面并非理想平面且在试验过程中发生不均匀变形。
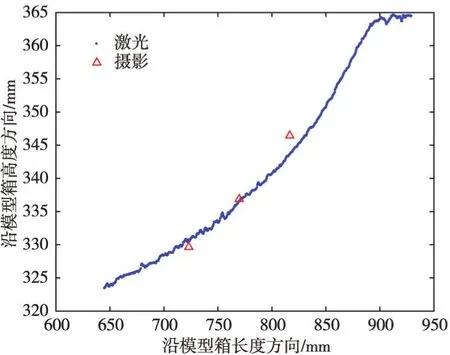
图16 由激光传感器与三维摄影测量技术测量得到的结果对比
相比于激光传感器,三维摄影测量技术除了可以监测模型的沉降,还可以得到模型表面标记点在其它方向上的位移,这对分析模型的整体变形乃至破坏过程具有指导性的意见。由三维摄影测量技术得到的模型中轴线上各标记点在沿模型箱长度、高度两个方向上的最终位移如图17所示,说明坝体在向下沉降的同时,还会侧向移动,坝体变形不均匀,最终发生破坏。
因此,本文提出的三维摄影测量技术可适用于土工离心模型的变形监测,应用该技术可以实现对模型某个区域变形过程的监测,为分析模型的变形以及破坏提供依据。
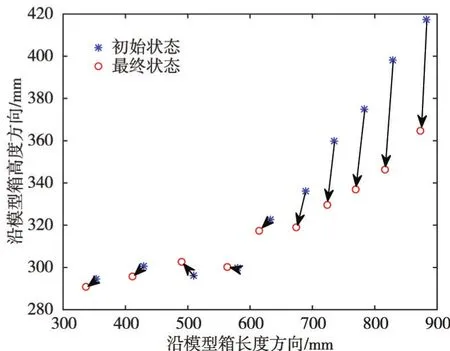
图17 土石坝模型中轴线上各标记点的最终位移
4 结论
(1)本文提出了三维摄影测量技术并将其应用在离心模型试验中,可以实现变形的三维监测,目前在土工离心模型试验中应用的摄影测量技术仅限于对模型平面变形的测量。(2)本文提出的三维摄影测量技术应用到软基土石坝的离心模型试验中,试验中还采用了激光位移传感器进行模型监测,试验结果表明两种方法测得的变形趋势一致,数值相近。表明本文提出的技术可以应用于离心模型试验。(3)为了进一步在土工离心模型试验中推广应用三维摄影测量技术,还需要提高测量精度,具体措施有:将用于标定摄像机参数的标记点设在模型箱壁上,每一步计算前均重新标定摄像机的参数;试验中架设3台摄像机,校正计算结果;考虑并解决由于摄像机畸变而引起的系统误差。
