基于水动力模型的花园湖行洪区优化调度研究

马娇娇，李瑞杰，宋昊明，谭炳卿，李 奎

（1.中工武大设计研究有限公司安徽分公司，安徽合肥230000；2.中水淮河规划设计研究有限公司，安徽合肥230601；3.合肥工业大学土木与水利工程学院，安徽 合肥230009）

淮河干流行蓄洪区在防洪体系中发挥着重要作用，运用后能够有效降低河道洪水位、减轻上下河段防洪压力。但随着区内经济发展、人口密度增加，淮河干流行蓄洪区在历年的洪水调度中运用困难，大多数行蓄洪区都存在超指标运用或超指标仍未启用的情况，一定程度上影响了行蓄洪时机。为充分发挥行蓄洪区的作用，2008年开始实施《淮河行蓄洪区调整规划（修订）》。其中淮河干流蚌埠至浮山段原有4处行洪区进行调整：方邱湖改为防洪保护区，区内开挖分洪道；临北段退堤后改为防洪保护区；香浮段局部退堤后改为防洪保护区；花园湖局部退堤并建进、退水闸，改为有闸控制的行洪区。蚌埠至浮山段河道及行洪区平面示意见图1。通过规划调整，减少了淮河干流上的行洪区，扩大了河道滩槽泄量，提高行洪区启用标准，保证行洪区行洪效果。调整规划中部分工程已实施完成，为更好地发挥行蓄洪效果，研究制定规划实施后花园湖行洪区调度运用方案具有重要意义。

图1 蚌埠至浮山段河道及行洪区

1 洪水演进数学模型

淮河中游河势较为复杂，有单一河道、行洪区和湖泊。水动力模型研究范围为淮河干流蚌埠至浮山段，规划实施后该河段包括花园湖行洪区，整个河段形成由河道和行洪区组成的复杂河网水系。干流河道建立河网一维模型，行洪区建立平面二维模型，通过对一、二维模型的耦合，将干流河道与行洪区进行连接，对干流河道向行洪区分洪及行洪区向河道退水的洪水演进情况进行模拟，建立行洪区不同启用条件下的水位—流量关系，从而对调整规划实施后行洪区启用条件进行合理性分析及优化。

1.1 河道一维水动力模型

1.1.1 模型构建

一维河网模型以蚌埠至浮山段河道为计算范围，经概化后河网总长93.3 km，断面数据采用吴家渡至浮山段规划河道断面资料，共设置断面443个，断面间距为200～450 m。计算边界选取吴家渡为上边界，并且给定吴家渡1954年型100 a一遇还原洪水流量过程线；浮山为下边界，同时给定浮山站历年实测水位—流量关系，当淮河干流流量为13 000 m3/s时，浮山达到设计水位18.5 m。

行洪区进、退洪闸闸门处分别设置2个分叉河道，用于模拟干流河道向行洪区内进洪以及行洪区向干流河道退洪的过程。闸门类型设置为底流，并且均以“时间”作为闸门控制方式，给定一个时间序列。此种方式能够较好地控制闸门开启的时间及速度，更加精确地模拟闸门的进洪及退洪情况。

该河段沿程分布的水文站见图2，图中使用1954北京平面坐标系（下同）。

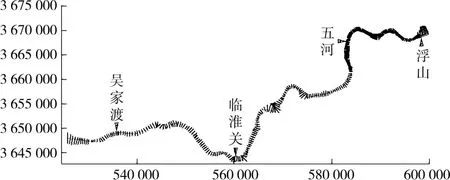
图2 淮河干流蚌埠—浮山段水文站分布

1.1.2 参数确定

模型参数的选取直接影响模型的模拟精度，河道糙率是建立水动力模型的重要参数，对计算结果影响较大，需以实测水文数据进行率定验证。模型参数选取参考相关研究成果［1］，并以典型年2007年实测洪水过程进行验证计算。通过选取沿程4个测站的计算水位过程线，与实测水位过程进行比较，以进一步确定糙率取值。选取糙率值见表1，验证计算的部分结果见图3。

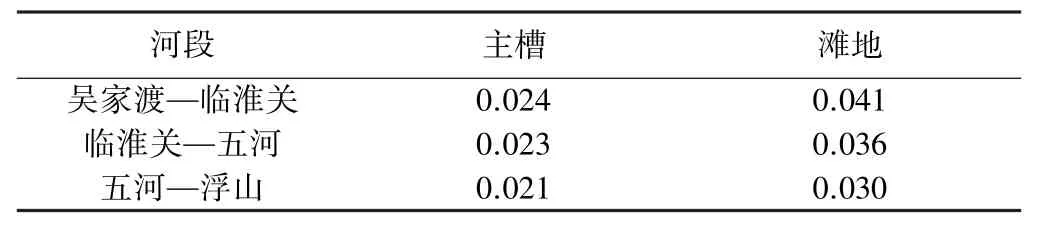
表1 蚌埠至浮山各河段糙率取值

由图3可知，沿程各测站水位计算值与实测值过程线的趋势是一致的，能够较好地反映2007年的洪水演进过程，模型的模拟精度较高，能够满足计算需求。

图3 2007年沿程测站水位实测值与计算值对比

1.2 花园湖行洪区二维水动力模型

二维水动力模型构建主要是mesh文件的生成及花园湖参数、模拟时间和初始条件的确定。根据花园湖地形资料，由网格生成器生成花园湖mesh文件，网格边长设置为100～200 m，共有约10 000个网格节点，能够满足模拟计算的需要。模拟时间步长60 s，时间步数86 400，计算时段与一维模型设置一致。初始条件中水面高程设置应与一维模型中进、退洪闸断面高程及初始水位相协调。行洪区二维网格地形图见图4。

二维水动力模型的主要参数是花园湖行洪区糙率，由于该行洪区1956年以后未启用过，缺乏实测水文资料，因此根据相关研究成果［1］以及本研究对花园湖二维模型的模拟计算，确定其糙率为0.04。

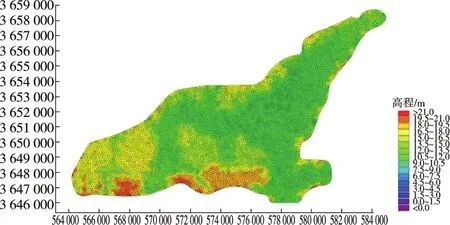
图4 花园湖行洪区网格地形

1.3 Mike Flood模型耦合

通过对干流河道建立一维模型、花园湖行洪区建立二维模型，进而用Mike Flood将一、二维模型进行耦合，连接方式采用标准连接，将一系列二维网格单元连接到一维模型中，既能够提高模拟精度和可靠性，又可以发挥一维模型快速方便的特点。一、二维模型耦合概化见图5。

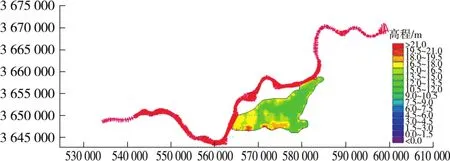
图5 研究区地形及河网一、二维耦合概化

2 规划实施后花园湖行洪区优化调度研究

2.1 调度方案选取

行洪区启用时机与方式对于其附近河道的水位、流量有较大的影响。花园湖行洪区的运用把控制站临淮关水位作为启用条件，为了对规划提出的启用条件进行合理性分析以及进一步优化，采用3种启用水位，分别是规划提出的21.1 m以及21.1 m±0.5 m；采用2种启用方式，模拟不同启用条件下的洪水演进过程。其中“先开启进洪闸，再开启退洪闸”的方式是进洪闸开启后，待行洪区内退洪闸处水位与退洪闸附近的干流河道水位一致时再开启退洪闸。不同组合情况下的花园湖行洪区调度方案见表2。

表2 花园湖行洪区调度方案

2.2 不同运用方案效果分析

在遭遇100 a一遇洪水情况下，按照不同启用时机及启用方式模拟河道及花园湖行洪区的洪水演进过程，对不同启用条件下行洪效果进行分析。各站计算水位过程线见图6～图8，行洪区启用后沿程测站计算峰值水位见表3。

表3 规划条件下行洪区不同调度方案计算峰值水位 m

由表3计算结果可以看出，方案三以临淮关水位到达21.60 m作为行洪区启用条件，开始进洪时，临淮关水位已接近洪峰，削峰效果比其他两种方案弱，洪峰水位较高。而采用方案一、二的启用条件对干流河道洪峰影响相同，其原因是方案一、二两种不同的启用条件对应进洪闸启用的时间分别是7月11日8：00、7月12日14：00，时间较为接近，两种不同启用时机对洪水过程的影响仅在行洪区启用初期差异较大，对洪峰水位的影响逐渐趋于相同。由于闸门启用方式相对于启用时机，对河道水位影响较小，且不同启用方式之间的差异在闸门启用初期较为明显，因此在方案一和方案二启用条件下两种启用方式沿程测站的洪峰水位相同。

2.3 调度运用方案的优化研究

2.3.1 启用方式分析

根据模拟计算结果，按照临淮关水位达20.6、21.1 m时启用花园湖行洪区，两种启用方式对沿程测站洪峰水位的影响相同，故进一步分析各站洪峰水位历时情况，以确定闸门最佳启用方式。按照规划提出的启用水位即临淮关水位达21.1 m时启用，由图9～图11可以看出，以进、退洪闸同时启用的方案开启闸门时沿程各站洪峰水位的历时较短。同样，按照临淮关水位达20.6 m时启用行洪区，经分析采用进、退洪闸同时开启的方式时各站洪峰水位的历时较短。而按照临淮关水位达21.6 m时启用花园湖，方案一相对于方案二，沿程各站洪峰水位较低。因此，在遭遇100 a一遇洪水时，淮河干流临淮关水位到达规定启用水位时，花园湖行洪区应当综合考虑进、退洪闸同时开启的闸门调度方式，此方式行洪效果相对较好。

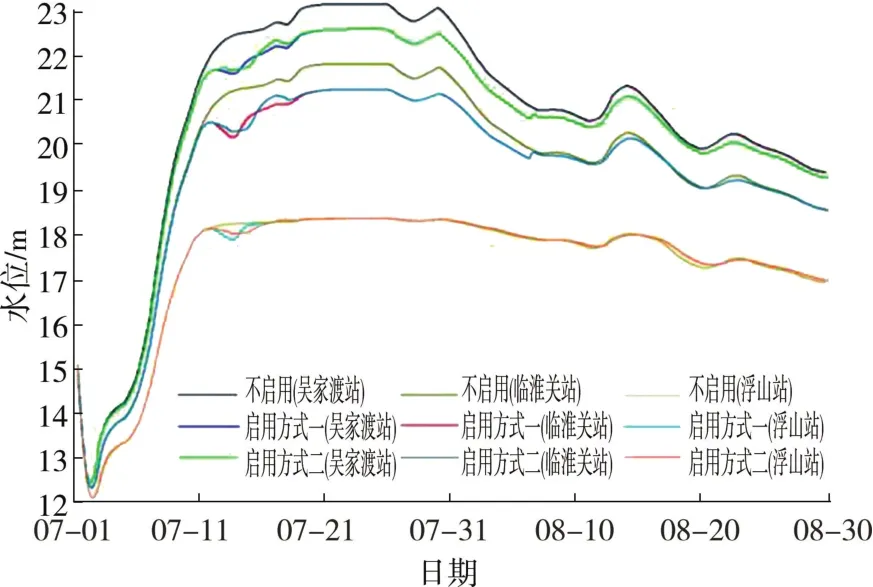
图6 1954年型100 a一遇洪水各站计算水位过程线（方案一）

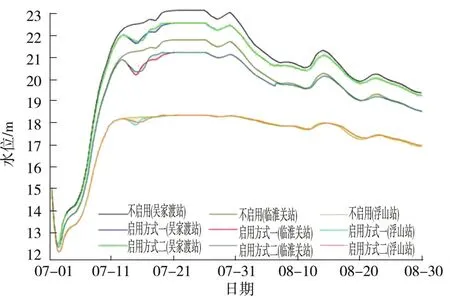
图7 1954年型100 a一遇洪水各站计算水位过程线（方案二）

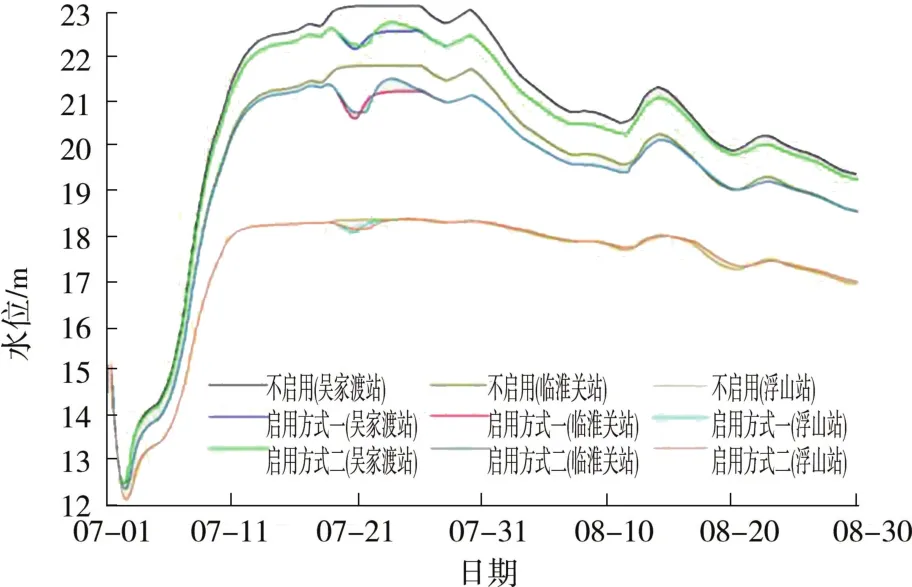
图8 1954年型100 a一遇洪水各站计算水位过程线（方案三）

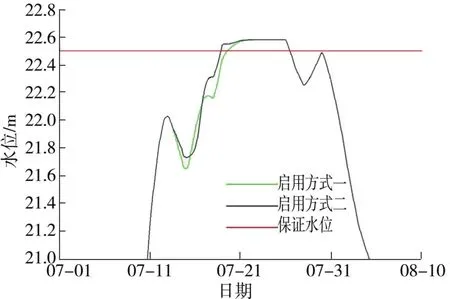
图9 规划条件下不同启用方式吴家渡水位过程线

图10 规划条件下不同启用方式临淮关水位过程线

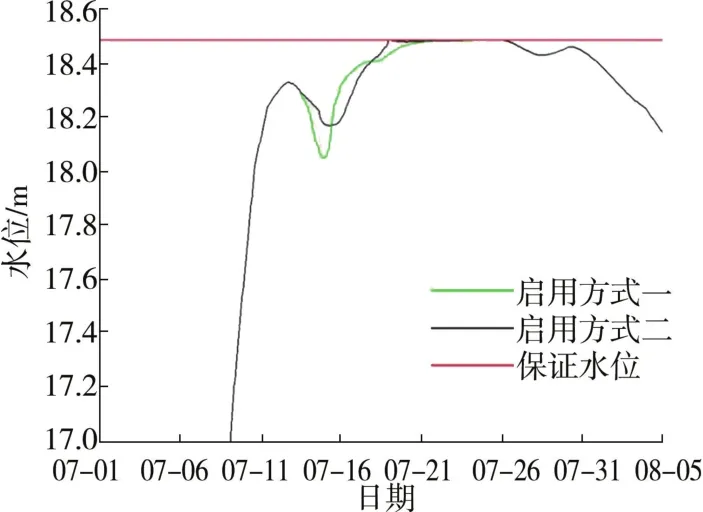
图11 规划条件下不同启用方式浮山水位过程线

2.3.2 启用时机分析

以方案三临淮关水位达21.60 m作为行洪区启用条件，行洪区运用后干流河道各站洪峰水位相对较高。采用方案一、二的启用条件对干流河道洪峰的影响相同，进一步分析两种不同启用水位下各测站高水位历时情况，对行洪区启用时机进一步优化。吴家渡选取21.70 m和22.10 m作为超高水位历时分析的水位，临淮关选取20.30 m和20.90 m，浮山选取18.10 m和18.30 m。根据上述分析，以进、退洪闸同时启用的方式进行闸门的调度运用。

表4为各站超高水位历时情况，在遭遇100 a一遇洪水时，按进、退洪闸同时开启的方式启用花园湖行洪区，方案一相对于方案二超高水位历时较短，行洪效果相对较好。

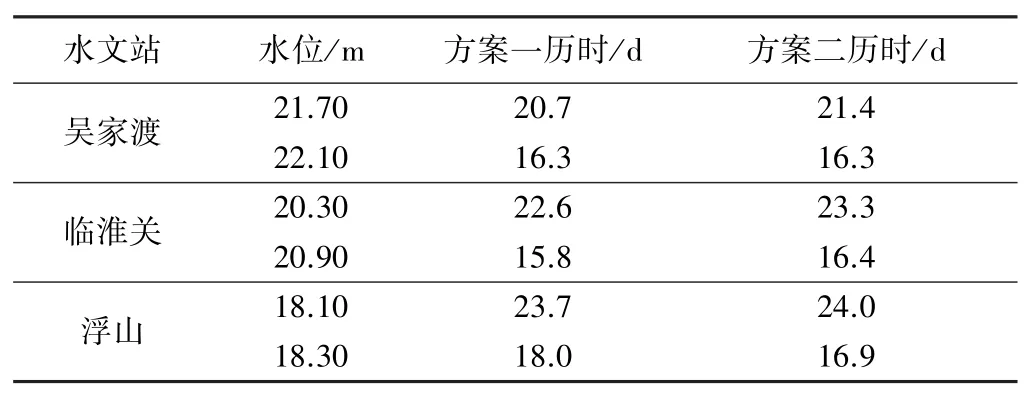
表4 规划条件下行洪区不同调度方案各站超高水位历时情况

3 结 语

对淮河干流河道建立一维模型，花园湖行洪区建立二维模型，通过耦合连接模拟100 a一遇洪水行洪区不同启用条件下的洪水过程。在规划河道条件下，利用典型年实测洪水过程对一维模型参数进行率定验证，模拟精度较高，模型可用于较复杂的洪水模拟计算。

研究结果表明，在规划条件下，遭遇100 a一遇洪水时，花园湖行洪区按照临淮关水位达20.60 m时启用，并且以进、退洪闸同时开启的闸门调度方式运用，行洪效果相对较好，能够较好地发挥行洪区的作用。但本次调度方案的优化研究未综合考虑行洪区启用后造成的经济损失、人员撤退转移等，在制定行蓄洪区调度运用方案时，应当充分考虑各方因素，处理好防洪与行蓄洪区发展的关系，使行蓄洪区受洪涝灾害的损失减少到最小。