“正方形中的圆”教学实录

2019-07-17张齐华

小学教学(数学版) 2019年1期

关键词：张老师正方形直径

◇张齐华

一回顾梳理，提出问题

师：今天这节课，我们一起来研究“正方形中的圆”（板书课题）。如何在正方形中画尽可能大的圆，相信同学们已经有了自己的认识。谁愿意和大家分享？

……

师：那么,你们能在正方形中画2 个尽可能大的圆吗？2个圆必须同样大，还不能有重合的部分。想不想试一试？

生：想！

二尝试探究，遭遇挫折

师：拿出作业单，先想象一下这2 个圆可能在哪里，大概有多大。有思路了，再动手试一试。如果独立完成有困难，也可以四人小组共同商量思路，然后给出你们的答案。

（学生独立思考后，组内交流，尝试着给出答案。随后，全班展示）

师：谁愿意带着你们小组的作品，和大家分享？

生：我们小组是这样的。先把这个正方形分成2 个同样的长方形，然后，在每个长方形里画了一个最大的圆（如图1）。这2 个圆不可能更大，而且也一样大。我们觉得，这就是正方形里能够画的2 个最大的圆。

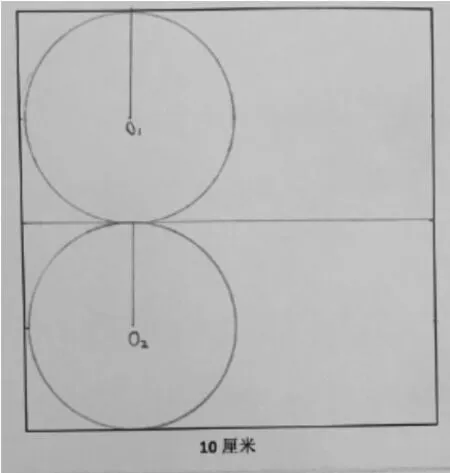
图1

师：还有不一样的思路吗？

生：我们小组是这样的。因为正方形不可能分成2 个同样大小的小正方形，所以，我们先把正方形分成了4 个同样的小正方形，然后，我们在其中2 个小正方形里画了最大的圆。我们觉得，这就是正方形里能够画出的最大的2个圆。（如图2）

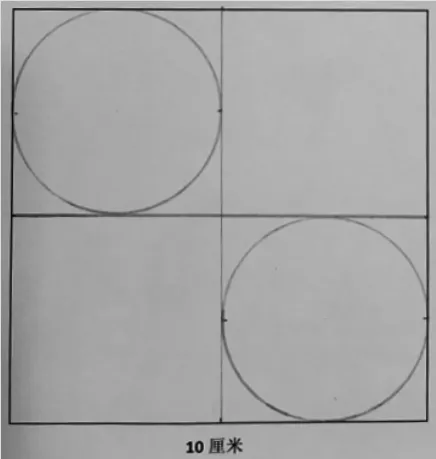
图2

师：还有不同的思路吗？（没有学生再举手。教师巡视全班，剩下的小组要么作业纸上一片空白，要么有一些画过的痕迹，但也被擦掉了）那行，关于屏幕上的这两种思路，有什么想法？谁来评价？

生：我觉得这两种思路都很好，画出来的圆，也都是正方形里最大的2 个圆。

生：我有不同意见。我觉得第一种方法不对，画出来的圆不是最大的。如果我们把这个圆（下面的）移到最右边，这时，2 个圆之间就会有很大的空隙。这样，我们就可以把这2 个圆画得更大一些！

师：闭上眼睛，在头脑里想象一下，你们觉得他的想法有道理吗？

生：有！

师：看来，这2 个圆，肯定不是正方形里所能画的最大的2 个圆。还有谁想继续评价？

生：我觉得第二种方法也不对。大家看，如果我们把这个大正方形中间的十字线去掉，就会发现，这2 个圆中间也有很大的空隙。也就是说，这2 个圆实际上还可以画得更大！

生：而且，第二种方法画出的圆和第一种方法画出的圆一样大。第一种方法错了，第二种方法肯定也是错的！

师：现在看来，这两种方法都是错误的。不过，老师希望大家先给这两个小组最热烈的掌声！（学生掌声）大胆猜一猜，明明错了，为何我们还要给他们热烈的掌声？

生：因为他们敢于尝试。

生：因为老师以前说过，错误也是一种资源，我们可以从别人的错误中学到东西。

生：我觉得至少他们已经开始思考了。

师：是的！刚才，张老师巡视了一圈，全班同学中，除了这两个小组给出了自己的思考，剩下小组的学习单上，要么什么都没有，要么只留了一些画过的痕迹，但最终也给擦掉了。老师很好奇，为何你们的作品上什么都没有？

生：因为我们不知道这个问题到底该怎么解答。

生：我们觉得，要想画出最大的2 个圆，必须得找到正方形。就像前面我们说的，正方形里之所以能够画出4 个或9 个圆，是因为正方形可以分成4 个或9 个小正方形。但现在，正方形怎么都不能分成2 个同样的小正方形。

生：我们小组其实一开始的思路和屏幕上的第二种方法一样。但画完以后，同桌就提出来，这2 个圆不是最大的，还有比它们更大的圆，就像刚才那位同学所说的那样。所以，我们最后还是把它们给擦了。

三再度探索，多样表达

师：因为找不到确切的思路而交了白卷；或者发现原有的思路不合适，又找不到更好的思路，而最终选择了放弃。这无疑是非常遗憾的！张老师送大家两点建议。第一，如果你实在找不到解决问题的确切思路，不妨回到最原始的方法——尝试，不合适就调整，再尝试，再调整。慢慢地，你就会发现，答案离你越来越近。第二，如果你实在找不到最准确的答案，没关系，你至少可以先找一个比较接近的答案。请大家一定记住，有总比没有好。愿意接受张老师的这两点忠告吗？

生：愿意！

师：那行，带着这两点忠告，再一次回到你们的学习单上，看看这一回，你们又可以获得哪些新的进展。

（学生再一次小组合作展开研究。研究过程中，有一个小组提出，想借助电脑进行探索，教师同意了他们的请求。研究结束后，全班汇报）

生：我们小组经过研究，发现这2 个最大的圆，它们的半径应该比2.8 厘米要大一点点。我们先画了2 个半径2.5厘米的圆，但发现它们还不是最大的，中间还有空隙。于是，我们把圆规的两脚稍微张大了一点，又画了2 个圆，发现好像还有点小。然后，我们又把圆规的两脚稍微张大了一点，这一次，我们感觉很接近了。我们量了一下，这2 个圆的半径大约是2.9 厘米。（如图3）

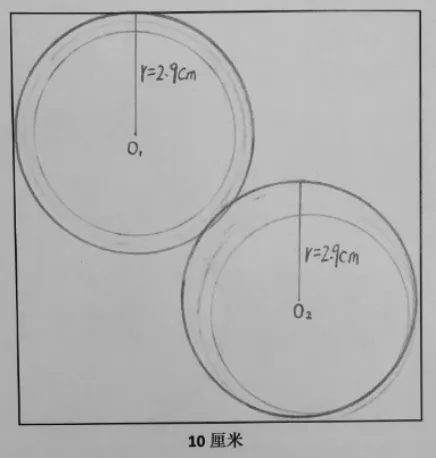
图3

生：我们小组也是这样尝试的。但是在调整的过程中，我们发现，一不小心，我们的圆就画到正方形外面去了。然后，我们就再调整，争取把圆画在正方形的里面。经过尝试，我们最后画出的圆，半径是2.8 厘米左右。

生：我们小组经过尝试发现，这2 个圆的圆心，肯定在正方形的对角线上。所以，我们就先画了一条对角线，然后在上面尝试着确定圆心（如图4）。画完后，发现不行，还嫌小，然后我们继续调整。最后，我们发现，这2个圆的半径都在2.9 厘米左右。

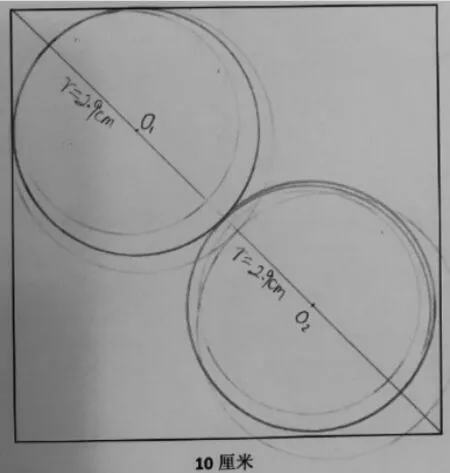
图4

生：我们的方法和他们有点类似。通过前面两个小组的交流，我们发现，这2 个圆的直径肯定比5 厘米大。于是我们就决定先试一试直径6 厘米。结果发现，直径6 厘米稍微大了点。于是，我们又决定试一试直径5.5 厘米，发现直径5.5 厘米又小了点。然后再试一试直径5.7 厘米。结果发现大小差不多了。所以，我们觉得，这2 个圆的直径差不多是5.7 厘米。

生：通过观察前面几个小组的汇报，我发现一个规律。其实，我们只要把这个正方形分成2 个同样大的三角形，（如图5）然后，只要想办法在每个三角形里画出最大的圆就可以了。

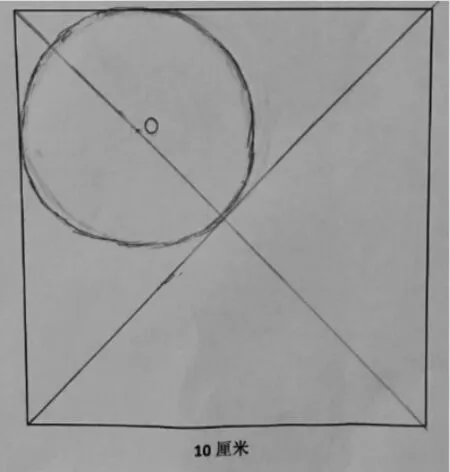
图5

师：把在正方形中画最大的2 个圆，转化成了在等腰直角三角形中画最大的1 个圆。真好！当然，只凭我们现在所学的知识，这个问题还是没办法解决。但是到了初中，利用平面几何的有关知识，这个问题就变得非常简单了！回顾刚才的学习过程，从一开始大家都无所适从，到现在，每一个小组都找到了属于自己的答案。虽然这个答案离准确的答案还有一点点距离，但至少已经相当接近了！张老师真心为大家点赞！不过，刚才还有一个小组借用了我的笔记本电脑，说可以在电脑上进行探索。你们又是如何探索的，有结论了吗？

生：我们在Word 文档里先画了一个边长10 厘米的正方形，这个尺寸是可以通过数据来设置的。然后，我们又画了2 个直径5 厘米的圆。画完后，我们一调整位置，果然发现直径5 厘米的圆不是最大的。于是，我们又通过调整数据，画了2 个直径5.5 厘米的圆，发现好像还不够大，还有空隙。然后，我们又继续调整数据，最终，我们发现，当圆的直径差不多是5.85 厘米时，这2 个圆才是最大的。

师：厉害！电脑作图，调整起来特别方便，数据也更精准。当然，这里的5.85 厘米可能还不是最后的答案，真正的答案究竟是多少，也许还有待于我们继续进行深入的研究。