基于验潮数据的全球平均海面高模型精度分析

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266590； 2.中国测绘科学研究院，北京 100830；3.海军工程大学 导航工程系，武汉 430033)

平均海平面(mean sea surface，MSS)是研究垂直基准、海图基准和海平面变化的重要参考面[1]。相对于参考椭球，它由大地水准面高和海面地形组成，被广泛应用于大地水准面、地壳形变[2]、中尺度涡探测和大洋环流[3]等问题的研究。因此，平均海面高的确定一直是大地测量学和物理海洋学研究[4]的基础问题，全球平均海面高模型精度及其分辨率的研究也显得格外重要。

卫星测高作为一种空间大地测量技术，因其全天候、可重复作业及覆盖范围广等优势[5]，极大提高了海面高数据的时空分辨率，从而改善了全球平均海平面高模型的精度及分辨率，提供了更为丰富的海洋信息[6-7]。自上世纪70年代中期，第一颗测高卫星Geos-3发射以来，国内外相关领域的学者及机构就开始利用卫星测高数据建立区域或全球平均海平面模型展开一系列的研究。Basic等[8]基于Geos-3和Seasat卫星数据建立了全球平均海平面模型MSS-9012，测高精度达到米级。随着ERS-1、 TOPEX/Poseidon(T/P)、Geosat、ERS-2、GFO、Jason-1、Envisat、IceSat、Jason-2、CryoSat-2、Saral、HY-2A、Jason-3等[9]测高卫星的陆续发射，测高数据的时间及空间分辨率也得到了极大改善。随着多源卫星测高数据融合技术的发展，平均海面高模型精度也逐渐提高到厘米级，如OSU95 MSS、GFZ MSS95、CLS01、DNSC08等[10]。目前，精度较高且常用的全球平均海面高模型主要有DTU13[11]、CLS15以及WHU2013[12-13]。三个模型所使用的数据都是从1993年到2012年跨度约为20年的多源卫星测高融合数据，其中WHU2013和CLS15模型测高卫星覆盖纬度均在80°S～84°N范围内，DTU13模型高卫星覆盖纬度在90°S～90°N范围内。WHU2013模型的格网分辨率为2′×2′，DTU13和CLS15模型的格网分辨率为1′×1′。

目前，在深海海域，卫星测高精度可达厘米级。但在近海，卫星接收的测高回波受陆地和地球物理环境的综合影响，数据质量大大降低，甚至无法使用[14-15]。验潮站分布于岸边，近海数据测量精度较高，但验潮数据的起算面是当地水尺零点，与卫星测高采用的大地高不同。因此，全球平均海平高模型近海精度的分析非常重要。本研究对比分析WHU2013、DTU13和CLS15三种全球平均海面高模型在全球海域的差异。从全球选取89个验潮站，利用GPS观测统一验潮数据的高程基准。再通过参考椭球和参考框架的转化，在同一基准下对三种模型海面高与验潮站得到的海面高进行比较，并着重分析了三种模型在全球范围内的近海精度。

1 数据及方法

1.1 验潮数据的处理

全球范围内验潮站的实测水位数据可以从平均海面永久服务(permanent service for mean sea level，PSMSL)网站(http://www.psmsl.org/)下载得到。WHU2013、DTU13和CLS15三种全球平均海面高模型的建立采用由T/P、Jason-1、Jason-2等多源测高卫星从1993年到2012年测高数据。月球近点轨道周期为8.847 a，月球轨道升交点运动周期为18.621 a，因此验潮数据至少要有18.6 a的资料[16]。本研究所用的验潮数据均选取各验潮站从1993年到2012年共20年的月平均观测数据。T/P卫星的轨道倾角为66°，考虑到T/P卫星的覆盖范围，在全球66°S～66°N区域范围内选取89个验潮站，其中太平洋56个验潮站，大西洋20个验潮站，地中海13个验潮站，其分布如图1所示。

有些验潮站数据有缺失，从PSMSL网站上下载的验潮月数据的缺失值皆以极值-999 99填充。当验潮站20年的月平均观测数据有缺失值时，对缺失数据进行线性插值。然后对插值后的验潮月数据进行粗差处理。正常情况下，海平面的变化比较缓慢，相邻两个月的验潮数据变化不大，当某个月的验潮数据突然增大或减少，此月的验潮数据就可以看作由某种原因造成的粗差。所以本文以三倍标准差作为极限误差对粗差进行探测并剔除，剔除率为1.56%，再对剔除的数据进行线性插值。最后对验潮月数据取平均值，得到每个验潮站验潮数据的年平均值。

验潮数据是海平面相对于验潮零点的变化量，结果受到陆地沉降和近海地形的严重影响，因此单独利用验潮资料无法得到绝对海平面[17-19]。WHU2013、DTU13和CLS15三个模型是采用大地高表示海面高。本文利用验潮站附近的GPS观测，计算各验潮站零点的大地高，然后加上验潮数据所计算得到的月平均海平面高，从而求得验潮站附近海面的大地高。

图1 选取的验潮站分布

1.2 全球平均海平面模型

WHU2013模型所使用的测高数据包括T/P、Jason-1、Jason-2、ERS-2、ENVISAT、GFO等卫星重复周期观测数据，为了提高空间分辨率还利用了ERS-1和Jason-1的大地测量任务数据、Cryosat-2的低分辨率观测模式的观测数据[13]。DTU13模型是由丹麦技术大学构建的(ftp://ftp.space.dtu.dk/)，使用的测高数据包括T/P、Jason-1、Jason-2、ERS-1、ERS-2、ENVISAT等卫星重复周期观测数据，为了提高空间分辨率还用到了Jason-1大地测量任务数据、Cryosat-2的合成孔径干涉雷达测量模式的观测数据[11]。CLS15模型数据可以从AVISO网站(https://www.aviso.altimetry.fr/en/home.html)下载得到，该模型数据包括T/P、Jason-1、Jason-2、ERS-1、ENVISAT、GFO、CryoSat-2等观测数据，并对其白噪声、长波长偏差以及海洋变率的不确定性进行了噪声预处理[20]。所有卫星测高数据都进行了海洋时变校正，这大幅度减少了海洋变率的影响，使得任意时期的平均海洋变化均匀化。

验潮站分布在岸边，一般不在全球平均海面高模型格网点处。通过验潮站的坐标，找到相应的模型格网，采用三次样条插值方法由格网点平均海面高计算得到各验潮站处的模型值。验潮站大部分都处于陆地与海洋的交界处，为了提高插值精度，所使用的格网点的数据需要来自海洋。本研究所使用的验潮站有89个，采用人工判别，根据验潮站在地图上的实际地理位置，从WHU2013、DTU13和CLS15三种全球海面高模型中选取相应的海面格网点进行三次样条插值。

1.3 验潮数据与平均海面高模型数据的基准统一

由于卫星测高数据所采用的T/P参考椭球与验潮站附近GPS所采用的参考椭球GRS80不同，所以本文将卫星测高提供的海面高数据转换到GRS80参考椭球上，转换公式为：

(1)

(2)

其中：a和e分别为T/P参考椭球的长半轴、第一偏心率；B和h分别为T/P参考椭球下的大地纬度、海面高；BG和hG下标分别表示GRS80参考椭球下的大地纬度、海面高；N为卯酉圈曲率半径；M为子午圈曲率半径；da=aG-a=0.7 m，aG为GRS80椭球长半轴；dα=αG-α=0，αG为GRS80椭球扁率，α为T/P椭球扁率之差[21]。

卫星测高数据所采用的参考框架与验潮站附近GPS所采用的参考框架ITRF08不同，需要进行参考框架转换，转换公式为

HT/P=HITRF08+Δxcosφcosλ+Δycosφsinλ+Δzsinφ+f。

(3)

其中，HT/P为卫星测高得到的海面高，HITRF08为ITRF08框架下验潮数据计算的海面高，λ和φ为对应点的经度和纬度，Δx、Δy、Δz和f分别为原点的三个平移参数和一个偏差因子，利用最小二乘法求得这4个参数[3]。

2 结果与分析

2.1 三种全球平均海面高模型比较

2.1.1 海域差异及原因

为了比较WHU2013、DTU13和CLS15三种全球平均海面高模型在海域范围内的差异，三种模型在全球海域进行比较分析。对三个模型计算的海面高求差，并剔除大于3倍中误差的模型差值以避免粗差的干扰，其差值结果如图2所示。

图2(a)～(c)分别为WHU2013、CLS15、DTU13三种全球平均海面高模型在66°S～66°N海域内的海面高差异。从图中可以看出，WHU2013与CLS15差异最小，两种全球平均海面高模型的一致性最好，WHU2013与DTU13的差异最大。造成这种现象的原因总结如下：

1) 从三个模型采用的测高数据来看，WHU2013与CLS15均采用了相同的重复周期观测数据(T/P、Jason-1、Jason-2、ERS-2、Envisat、GFO)，相比于 WHU2013与CLS15采用5种重复周期观测数据，DTU13在此基础上还采用了Icesat和Geosat的重复周期观测数据；

2) 从模型数据的处理方式来看，三种模型虽然采用了相同的非重复周期观测数据(ERS-1、Jason-1、Cryosat-2), 但WHU2013与CLS15对非重复周期观测数据进行了海面高时变校正，而DTU13没有对非重复周期观测数据进行海面高时变校正，直接通过交叉点平差对非重复周期观测数据进行处理；

3) 从模型格网的划分来看，WHU2013格网分辨率为2′×2′，DTU13与CLS15的格网分辨率为1′×1′。WHU2013与 CLS15的覆盖范围为80°S～84°N，且两种模型测高数据格网化的方法均采用最小二乘配置法。WHU2013模型的格网点与CLS15模型的格网点重合，而DTU13的覆盖范围为90°S～90°N，与WHU2013和 CLS15模型均没有重叠格网点。所以本研究对DTU13模型进行比较分析的数据点均由模型格网点线性插值得到，数据处理结果可能引入插值误差。

从图2(a) ～ 2(c)还可以看出，三种模型在日本海域、墨西哥湾、菲律宾群岛海域、阿古拉斯海流区域的差值均较为明显。这是由于这些区域靠近陆地，岛屿较多，地理环境复杂，且受洋流(如黑潮、墨西哥湾流等)、厄尔尼诺/拉尼娜现象等影响较大，测高精度明显下降，从而海面高模型在这些区域的精度低于其他海域。

2.1.2 近海、远海及全球海域差异

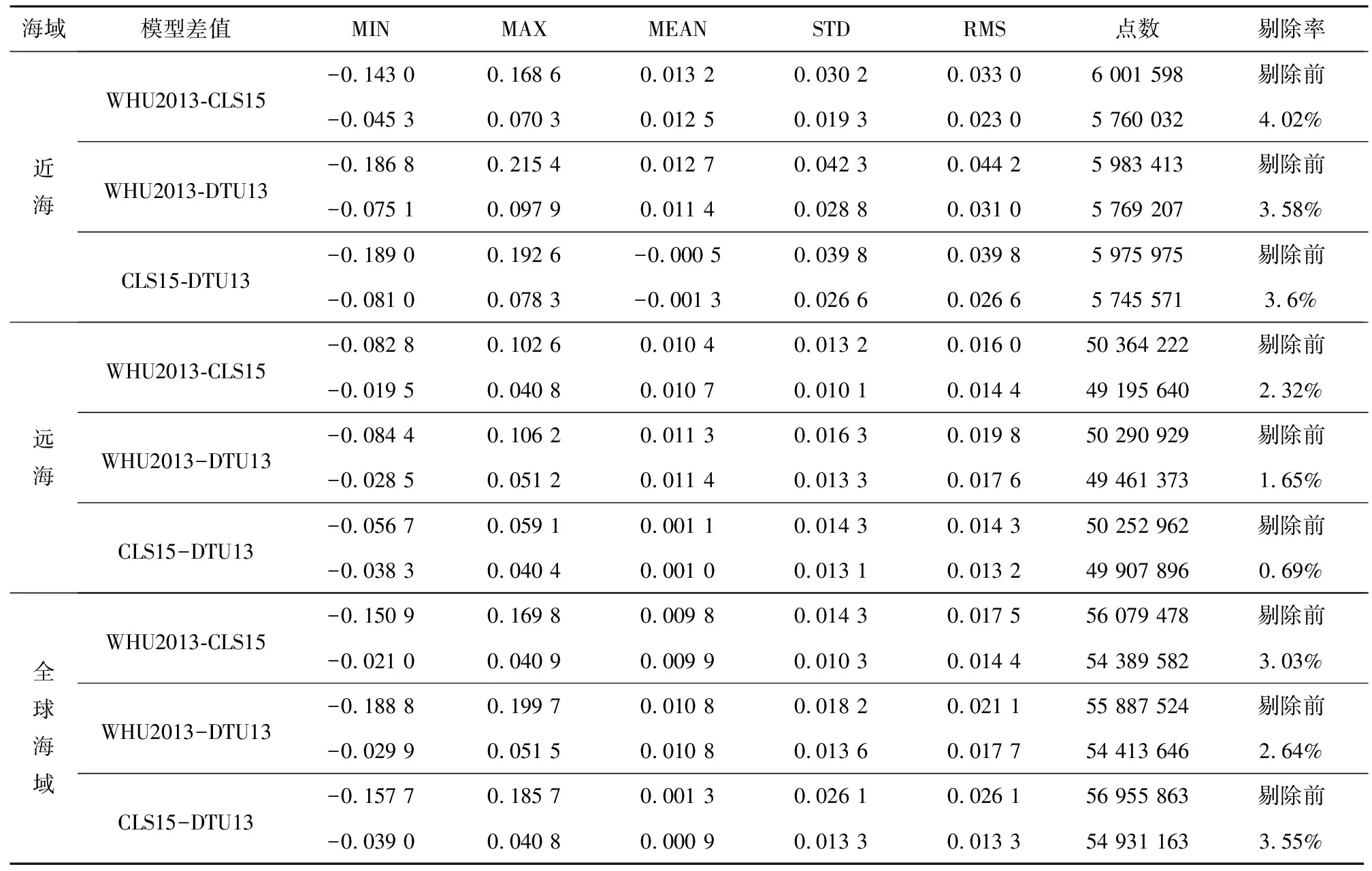
为了更加清晰直观地分析三种全球平均海面高模型在近海、远海及全球海域的差异，对三种模型分别在近海、远海及全球海域进行比较分析，其中近海区域选择的是海岸线平行向外100 km的海域。为避免粗差的干扰，剔除了大于3倍中误差的模型差值，差值统计结果如表1所示。

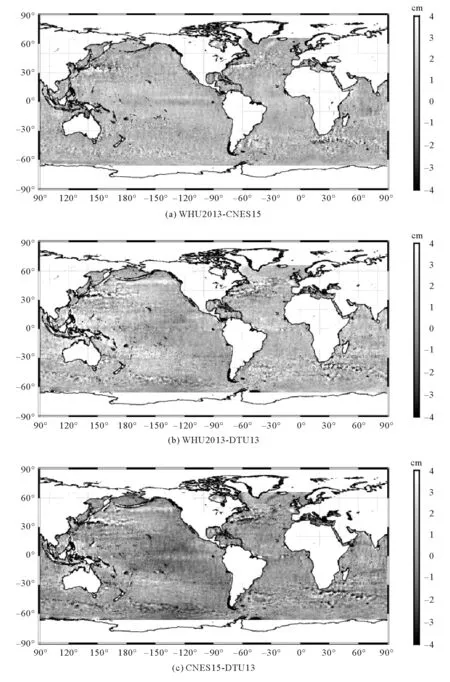
图2 三种全球平均海面高模型海面高差异

表1 三种全球平均海面高模型间海域差异统计

Tab.1 Statistics of differences of sea surface height between three global mean sea surface height models m

海域模型差值MINMAXMEANSTDRMS点数剔除率近海WHU2013-CLS15-0.143 00.168 60.013 20.030 20.033 06 001 598剔除前-0.045 30.070 30.012 50.019 30.023 05 760 0324.02%WHU2013-DTU13-0.186 80.215 40.012 70.042 30.044 25 983 413剔除前-0.075 10.097 90.011 40.028 80.031 05 769 2073.58%CLS15-DTU13-0.189 00.192 6-0.000 50.039 80.039 85 975 975剔除前-0.081 00.078 3-0.001 30.026 60.026 65 745 5713.6%远海WHU2013-CLS15-0.082 80.102 60.010 40.013 20.016 050 364 222剔除前-0.019 50.040 80.010 70.010 10.014 449 195 6402.32%WHU2013-DTU13-0.084 40.106 20.011 30.016 30.019 850 290 929剔除前-0.028 50.051 20.011 40.013 30.017 649 461 3731.65%CLS15-DTU13-0.056 70.059 10.001 10.014 30.014 350 252 962剔除前-0.038 30.040 40.001 00.013 10.013 249 907 8960.69%全球海域WHU2013-CLS15-0.150 90.169 80.009 80.014 30.017 556 079 478剔除前-0.021 00.040 90.009 90.010 30.014 454 389 5823.03%WHU2013-DTU13-0.188 80.199 70.010 80.018 20.021 155 887 524剔除前-0.029 90.051 50.010 80.013 60.017 754 413 6462.64%CLS15-DTU13-0.157 70.185 70.001 30.026 10.026 156 955 863剔除前-0.039 00.040 80.000 90.013 30.013 354 931 1633.55%

从表1可以看出，在近海区域，粗差未剔除前三种模型间差值最大值与最小值在0.2 m左右。三种模型所采用的海陆界线也不完全相同，在近海有部分模型值的陆地海洋归属不明确。为了避免粗差的干扰，利用3倍中误差对模型差值数据进行了剔除。粗差剔除后，在近海，WHU2013与CLS15差值的STD为0.019 3 m，WHU2013与DTU13差值的STD为0.031 0 m，DTU13与CLS15差值的STD为0.026 6 m，说明在近海区域WHU2013与CLS15的一致性最好。在远海，WHU2013与CLS15差值的STD为0.010 1 m，小于WHU2013与DTU13差值和DTU13与CLS15差值的STD，同时三个模型在深海区域的差值的STD都小于在近海区域模型间差值的STD。在全球海域，WHU2013与CLS15差值、WHU2013与DTU13差值和DTU13与CLS15差值的STD分别为0.010 3 m、0.013 6 m和0.013 3 m，模型间差值STD都大于其在深海区域，小于其在浅海区域。

从全球海域来看，无论是在近海还是远海，WHU2013与CLS15差值的STD都是三个模型间最小的，WHU2013与DTU13差值的STD最大。这说明在海域范围内，WHU2013与CLS15一致性最好，其次是DTU13与CLS15。剔除粗差后，三个模型间差值最大值与最小值都在厘米级，且差值的STD都在0.01～0.02 m左右，说明三个模型在全球海域具有较好的一致性，海面高模型数据结果也是可靠的。

2.2 基于验潮的海面高模型比较

2.2.1 差值范围统计

为了对WHU2013、DTU13和CLS15三个全球平均海面高模型在全球范围的近海精度进行评估，从全球选取了89个验潮站，首先利用验潮站附近GPS观测计算大地高，通过水准资料求得验潮站水尺零点大地高，将验潮资料转换为海面的大地高。 然后，将验潮站位置相应的模型格网通过三次样条插值，得到验潮站相应的模型海面高。 将验潮得到的海面大地高和对应的模型海面高进行比较，其差值统计结果如表2所示。

表2 三种模型与验潮资料所得海面高差值范围统计

在选取的89个验潮站中，采用三次样条插值方法，把WHU2013、DTU13和CLS15三种模型插值得到的验潮站点的海面高与根据验潮资料求得的海面高的差值分成4个范围(表2)，有46%的差值分布在0～0.1 m，36%的差值分布在0.1～0.3 m，仅有18%的差值大于0.3 m。

2.2.2 近海精度评定

将89个验潮站和三种全球海平面模型数据分区域处理，分别判别三种全球平均海面高模型在太平洋、大西洋、地中海以及全球的近海精度。精度评定的指标分别是模型海面高与根据验潮资料求得的海面高差值的最小值(MIN)、最大值(MAX)、平均值(MEAN)、均方根(RMS)以及标准差(STD)，统计结果如表3所示。

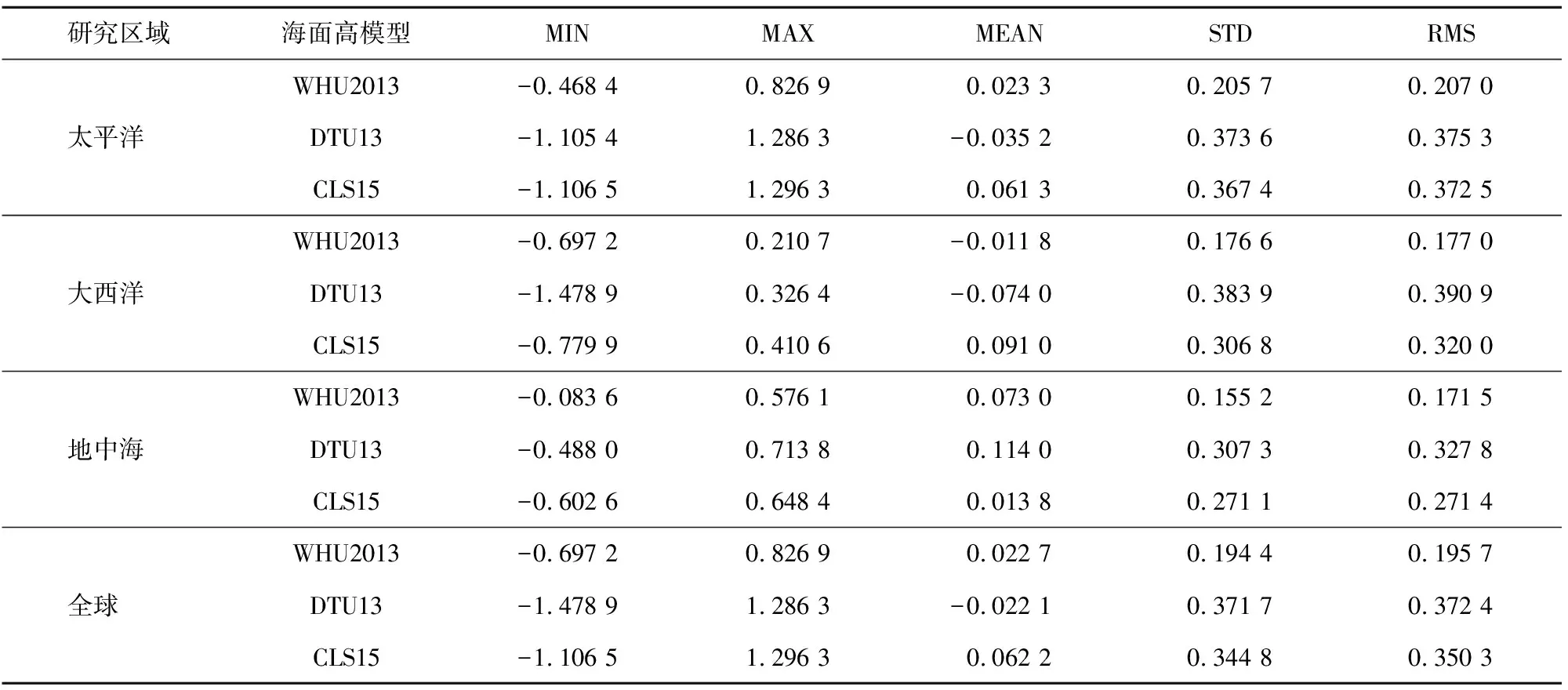
表3 基于验潮的三种模型精度评定统计

从表3可以看出，在太平洋海域，WHU2013模型的近海精度最高，其RMS为0.207 0 m，比DTU13和CLS15两种模型的RMS小约0.17 m。WHU2013模型的最小值为-0.468 4 m，最大值为0.826 9 m，而相比于WHU2013模型，DTU13和CLS15两种模型的最小值更小，最大值更大，说明DTU13和CLS15两种模型差值的振幅范围均大于WHU2013模型。CLS15模型的RMS为0.372 5 m，精度略高于DTU13模型。

在大西洋区域，WHU2013模型的RMS为0.177 0 m，精度最高；DTU13模型的RMS为0.390 9 m，精度最差。在地中海区域，WHU2013模型的RMS比DTU13和CLS15两种模型的RMS分别小约0.15 m和0.1 m，说明在此区域近海精度最高的模型同样是WHU2013模型，CLS15模型近海精度高于DTU13模型。在全球范围内看，WHU2013模型的RMS为0.195 7 m，精度最高，DTU13与CLS15两种模型的RMS分别为0.372 4 m和0.350 3 m，说明CLS15的近海精度略高于DTU13模型。

通过上述分析可以看出，三种全球平均海面高模型在太平洋、大西洋、地中海以及全球的近海精度研究结果是相同的，近海精度最高的是WHU2013模型，CLS15模型的近海精度略高于DTU13模型。WHU2013模型、DTU13模型和CLS15模型近海精度最高的区域都在地中海。

3 结论

研究了WHU2013、DTU13和CLS15三种全球平均海面高模型在66°S～66°N海域范围内的差异。并从全球选取89个验潮站，利用验潮站附近的GPS观测，统一验潮站的高程基准。通过参考椭球与参考框架的转化，将三种模型海面高分别与验潮站得的海面高在同一基准下进行对比分析，评定三种模型近海精度，为以后模型的使用提供一定的参考。结论如下：

1) 无论是在近海、远海还是全球海域，WHU2013模型与CLS15模型的一致性最好，WHU2013模型与DTU13模型差异最大。

2) 三种模型在远海的一致性均优于近海，且在气候及地理环境比较复杂的区域差异较大。

3) WHU2013模型的近海精度高于DTU13和CLS15模型，CLS15模型的近海精度略高于DTU13模型，三种模型近海精度最高的区域均为地中海。