基于非均匀变分节块法的pin-by-pin计算加速算法研究
2019-07-15张滕飞吴宏春曹良志李云召刘晓晶熊进标
张滕飞,吴宏春,曹良志,李云召,刘晓晶,熊进标,柴 翔
(1.上海交通大学 核科学与工程学院,上海 200240;2.西安交通大学 核科学与技术学院,陕西 西安 710049)
针对核反应堆三维全堆芯计算,传统的中子学模拟方法大多采用均匀化粗网的扩散理论[1]。相比于均匀化粗网的扩散理论,pin-by-pin计算既能更准确地描述组件内部的非均匀效应,又能获得栅元级别的高分辨中子学信息,有助于提高三维全堆芯模拟的计算精度和分辨率,是国内外反应堆物理研究的热点之一。近年来,pin-by-pin计算的相关均匀化理论已有长足发展,如SPH因子方法[2-3]、不连续因子方法[4]等,但另一方面,pin-by-pin计算的加速技术研究依然较少,大多情况下只能凭借并行计算手段提高计算速度[5-6]。实际的核反应堆堆芯由数以万计的棒束构成,采用pin-by-pin计算方法将产生百万量级的细网,对数值计算的收敛性和计算量提出了挑战,也制约了pin-by-pin计算方法的应用。研究表明,针对三维稳态压水堆堆芯问题的单核pin-by-pin计算,需约24 h的计算时间才能完成[5]。
为从算法层面上提高pin-by-pin计算的效率,基于三维扩散的非均匀变分节块法,本文分别从内迭代和外迭代两方面入手,应用粗网加速算法和粗网有限差分(CMFD)算法,研究加速pin-by-pin计算的方法。
1 理论模型
1.1 三维扩散的非均匀变分节块法
针对某一特定能群,在扩散近似下,偶阶中子扩散方程可写为:
(1)
式中:φ为节块内部中子通量密度;Ω为方位角向量;Σt为中子总截面;Σr为中子移出截面;q为中子源项。
根据变分原理,在由若干节块组成的整个求解域上,对应扩散方程的泛函可写作各节块内部及其表面上泛函的叠加贡献。在扩散近似下,各节块泛函可写为:
(2)
式中:Γ为外部边界;FV[φ,j]为各节块的泛函;V为节块体积;j为中子流;jn为每个节块表面的中子流。
利用x-y方向的有限元形状函数和z方向的正交多项式对节块内部中子通量密度、节块表面中子流分别展开,可得到节块内部的中子标通量密度矩求解方程及代表节块内部和表面响应关系的响应矩阵方程:
φ=-C(I-Π)j+Hq
(3)
j=(I-RΠ)-1Bq
(4)
式中:φ为中子标通量密度矩;q为中子源项展开矩;j为对应节块表面的中子流密度矩;I为单位矩阵;Π为转移矩阵,其中包含了问题中相邻节块的表面出射流和表面入射流的映射关系;H、C、B、R为响应矩阵,仅与节块的几何和材料分布相关。一般情况下,采用经典的红-黑迭代[7]格式求解式(4)以得到出、入射中子流密度矩,再代入式(3)得到中子标通量密度矩。
由于非均匀变分节块法在空间离散过程中采用了有限元形状函数,因此具备构造非均匀粗网的能力。图1示出3种不同的粗网剖分方案。以图1为例,1个17×17压水堆UO2燃料组件在径向上可有多种粗网剖分方案,即图1中的3种形式。图1中,灰色部分为控制棒导向管栅元,白色部分为UO2燃料栅元,黑色边界代表实际的栅元(材料)边界,红色边界为非均匀粗网边界。在各粗网中,所有栅元统一采用4个直角三角形有限元进一步剖分,并利用实际对应的栅元均匀化截面进行材料赋值。特别需要指出,17×17粗网剖分对应了传统pin-by-pin计算的均匀细网剖分方式,各粗网仅包含单一的栅元均匀化截面。
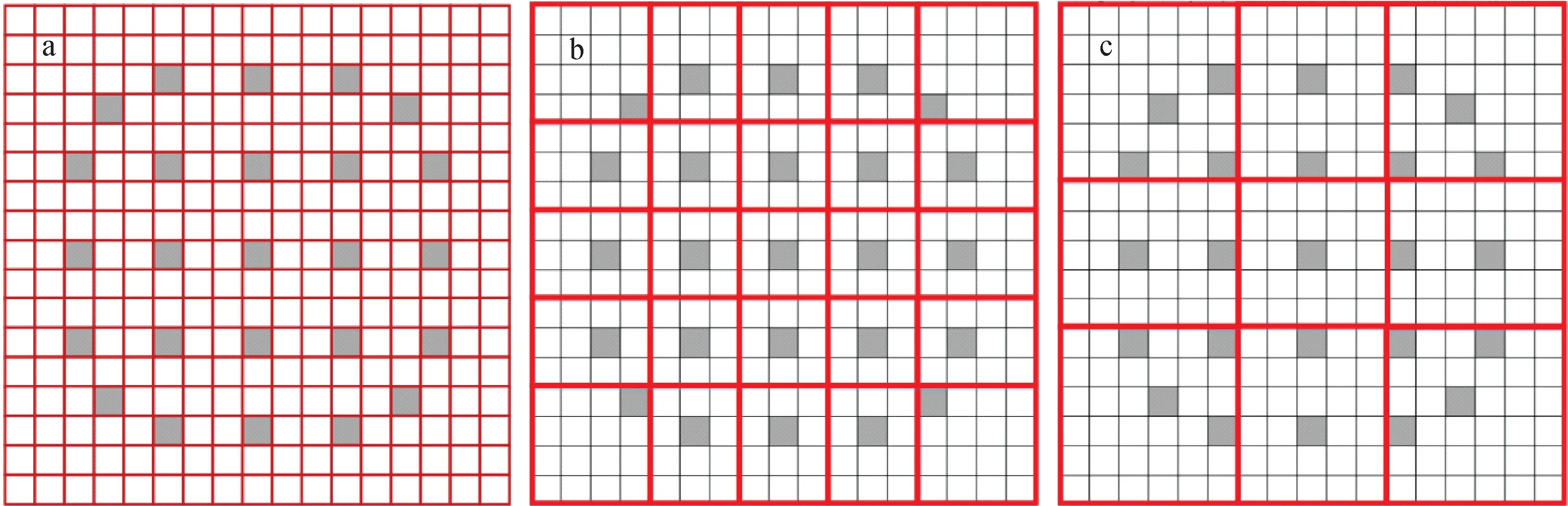
a——17×17;b——5×5;c——3×3图1 3种粗网剖分方案
1.2 内迭代的粗网加速方法
在非均匀变分节块法中,利用红-黑迭代格式求解式(4)的过程即为内迭代过程。内迭代处于整个求解过程的最内层,它的计算时间消耗由中子流展开向量j中所包含的未知量的个数决定,而未知量的个数与总的节块表面数目和表面展开阶数有关。将多个均匀化栅元合并为1个粗网能有效降低节块数目和节块表面数目,从而显著提高内迭代的计算效率。
1.3 外迭代的加速算法
粗网加速方法的使用会增加式(3)中更新中子通量密度矩的计算负荷。然而,一方面,不同于内迭代,每次外迭代仅进行1次中子通量密度矩的更新,其计算代价相对较小;另一方面,外迭代的加速技术较为成熟,容易实现高的加速比。因此,配合相应的外迭代加速算法,容易实现可观的加速效果。
众所周知,CMFD算法是最为常用且有效的外迭代加速算法之一,被广泛应用于非均匀计算方法如特征线方法(MOC)中[8-9]。CMFD算法利用有限差分假设下的粗网扩散计算结果来修正细网输运计算的结果,从而以较低的计算代价获得准确的计算结果。其中为了保证细网输运计算及粗网扩散计算之间的等价关系,利用细网输运的计算结果作为修正项对粗网扩散计算进行修正。本研究将CMFD算法[10]应用于非均匀变分节块法中,使每个非均匀粗网对应1个CMFD均匀粗网,并建立七对角CMFD矩阵方程进行求解。
矩阵分离(PM)算法[7]是变分节块法系列方法的经典加速方法之一,但传统PM算法仅能应用于内迭代的加速计算。本研究中重新建立了PM算法,将其同时扩展到内、外迭代中,称之为广义矩阵分离(GPM)算法[11]。PM算法和GPM算法的迭代流程对比如图2所示。其中,PM算法仅实现了对式(4)中响应矩阵方程的矩阵分离,因此只能加速红-黑迭代过程;而GPM算法则是将中子标通量密度矩求解方程和响应矩阵方程同时进行矩阵分离,不仅对加速红-黑迭代有效,且能加速裂变源项的收敛速度,从而起到加速外迭代的效果。
2 数值结果
采用栅元均匀化三维pin-by-pin问题对本研究的计算精度和计算速度进行验证。问题的三维几何与C5G7基准题[12]的不插棒布置相同,轴向等距离地划分为24层,截面为DRAGON产生的7群栅元均匀化截面[13]。在粗网加速计算中,采用图1所示的3种粗网划分方式进行计算。值得注意的是,非均匀粗网节块的表面中子流空间变化相比均匀细网计算更为剧烈,必须采用更高的径向表面展开阶数。经过对表面展开阶数的敏感性分析,本文针对17×17细网计算采用2阶表面展开,5×5粗网计算采用3阶表面展开,3×3粗网计算采用5阶表面展开,轴向统一采用2阶展开。以上离散阶数能保证3种粗网划分方式下的keff计算结果偏差低于10 pcm,栅元中子通量密度分布最大相对偏差不超过0.5%。此外,计算结果显示,CMFD和GPM算法并不会对计算结果产生不可忽略的偏差,故在本文中仅关注计算效率的对比。
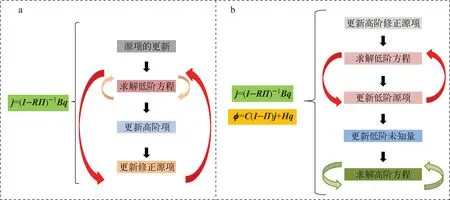
图2 PM算法(a)和GPM算法(b)的迭代流程对比
2.1 整体计算效率对比
pin-by-pin问题计算效率的对比列于表1。其中,CMFD/GPM计算时间代表求解CMFD或GPM算法所需的计算时间,整体求解时间代表求解整个三维问题所耗费的计算时间。由表1可见:不采用任何外迭代加速算法时,采用5×5和3×3粗网加速分别可将整体求解时间降低至细网计算的27%和34%;采用CMFD和GPM算法皆可有效地降低外迭代的次数。以17×17为例,采用CMFD和GPM算法分别将外迭代次数降低了88%和86%。然而,由于CMFD算法中需要直接求解耦合了三维粗网节块通量的七对角矩阵,在问题中节块数目过多时会严重影响计算效率:在17×17(pin-by-pin细网)的划分下,求解CMFD算法的计算时间甚至高达直接细网计算的12.70倍。此外,一方面,网格尺寸增大时,网格总数量降低,因此求解红-黑迭代(内迭代)的时间会有所减少;另一方面,网格尺寸增大时,外迭代收敛效果变差,外迭代次数增加。二者的平衡导致出现了5×5粗网加速效果最优的现象。综上所述,虽然GPM算法的外迭代加速效果稍差于CMFD算法,但其更适用于大规模问题的加速计算,且研究表明GPM算法的稳定性更优。当采用粗网加速时,CMFD和GPM算法皆可获得理想的加速比,最高可达10倍以上。
注:1) 计算时间按照17×17细网计算时间为1.00归一
2.2 外迭代的收敛趋势对比
不同算法外迭代收敛趋势的对比如图3所示。每次内迭代的时间体现为两次外迭代之间的时间差。由图3可见:粗网加速算法并不会对外迭代的总次数产生明显变化,但能有效减少每次内迭代所耗费的计算时间,从而加速整体的计算过程;两种外迭代加速算法均对减少外迭代总次数起到良好的效果,但显而易见,CMFD和GPM算法的求解过程将增加单次外迭代的时间。整体上,外迭代次数的减少仍占据主要影响,且可预见,当采用输运计算时,CMFD和GPM算法的求解时间占总计算时间的份额将进一步减小,从而实现更大的加速比。当采用GPM算法的5×5粗网和CMFD算法的3×3粗网计算时,加速效果最优。
3 结论与展望
基于三维中子扩散的非均匀变分节块法,本文提出一种加速pin-by-pin计算的思路,分别从内迭代和外迭代两个层面加速计算。利用非均匀几何的描述能力建立非均匀粗网剖分以加速内迭代,并应用了CMFD和GPM两种算法加速外迭代。数值结果表明,该方法能在保证精度的前提下,将pin-by-pin计算所耗费的时间降低10倍以上。后续的工作包括低阶输运计算功能及并行计算功能的实现。
