基于改进遗传算法的智能仓储多移动机器人协同调度

2019-07-15李文锋贺利军

武汉理工大学学报（信息与管理工程版） 2019年3期

范媛，李文锋，贺利军

(武汉理工大学物流工程学院，湖北武汉 430063)

随着电子商务行业的飞速发展，物流仓储内的订单拣选逐渐成为电商发展的核心环节。传统的“人到货”拣选模式中，60%～70%的时间都耗费在来回拣选货品上，且有较高的出错率。此外，当前电商行业订单结构的特点为品种多、批量小、批次多、周期短[1]，电商行业对物流仓储的拣选作业效率和准确率提出了更高的要求。现代智能仓储系统已采用“货到人”的拣选模式[2]，引入多移动机器人，将货品直接送至拣选台或拣选员，大幅度提高了拣选作业的效率，降低了拣选作业的出错率，减少了工人的劳动强度，降低维护成本并且使仓储空间布局具有良好的重构性。因此，构建基于多移动机器人的智能仓储系统已成为当下仓储物流研究的一大热点[3]。

多移动机器人的协同调度是实现构建基于多移动机器人智能仓储的关键。针对多移动机器人的协同调度问题，国内外学者已展开了较多的研究。蒋家志等[4]提出一种改进粒子群算法解决订单任务调度，考虑了多订单间的协同运输，提高了智能仓储的效率，但该模型未考虑多个移动机器人利用率的因素，导致其调度方案中单个机器人的能耗较高。沈博闻等[5]基于A*算法提出综合考虑路径代价和等待时间代价的机器人调度方法，实现多机器人的静态智能调度，但A*算法仅适用于小规模运算，无法解决多任务多机器人的情况。TRIGUI等[6]提出了扩展的分布式市场化算法来解决机器人任务分配问题，通过交换任务以提高工作效率，但其为局部调度，未考虑全局的最优性。MA等[7]根据仓库任务的特点，提出了全局任务先分组再重新分配的任务分组方法，将传统的静态分配算法应用于动态任务中，提高了全局任务路径均衡的性能。以上文献均是对多机器人进行任务分配和路径规划，但未考虑移动机器人电池的放电特性，以及移动机器人空载和载货时的耗电差异。

智能仓储多移动机器人在不饱和电量下进行“货到人”拣选作业，考虑移动机器人载货和空载时的耗电差异，将剩余电量作为机器人调度的约束条件，以多移动机器人作业总代价最小、作业代价均衡为优化目标，构建多移动机器人调度多目标优化模型。将改进遗传算法应用求解多目标优化模型，将多个任务分配至多移动机器人，实现多移动机器人协同调度，从而降低智能仓储多移动机器人作业成本，提高拣选作业效率。

1 智能仓储“货到人”拣选系统

智能仓储系统拣选作业为“货到人”模式，移动机器人接收上层控制系统(CCS)下发的任务序列，根据任务序列指令顺序搬运货架至拣选站台，待拣选人员将货物拣选完毕，再将货架搬运至原始位置。移动机器人的导航方式为二维码导航。移动机器人通过扫描货架上的二维码，获取货架坐标，扫描地面上的二维码，识别路径，并将自身位置信息和任务执行情况实时上传至CCS控制中心[8]。多个系统协同完成任务分配与多机器人调度的流程如图1所示。

图1 智能仓储任务分配与多机器人调度流程

智能仓储布局如图2所示[9]，从右向左依次为仓储货架区、高速运行区、排队等待区、拣选站台区，所有区域釆用网格排列的模式，多移动机器人在网格构成的环境中直线运行，每个巷道只能通过一个移动机器人。二维码位于每个网格的中心，移动机器人的步进距离为相邻两个二维码之间的直线距离，且通过二维码信息判断下一步的行驶方向。

图2 智能仓储布局图

图3 单机器人的行驶路径图

建立基于场景的坐标图，如图3所示。单个移动机器人分别搬运A、B、C、D、E这5个货架行驶至对应1～5号拣选台(纵轴上方框处)，每个机器人的移动单位为两个小圆点间的距离，箭头表示机器人的行驶方向。起点为坐标(0，1)，方案一的拣选顺序为A→B→C→D→E，方案二的拣选顺序为A→C→B→E→D。移动机器人运行过程中产生的自身代价定义为移动机器人从任务起点搬运货架至拣选台，再将货架搬运回原点产生的能耗代价，关联代价的定义为移动机器人以空载状态从一个任务节点行驶至下一个任务节点产生的能耗代价，其代价均与移动机器人的行驶距离成正比。两种调度方案产生的自身代价(方形内)和关联代价(圆圈内)如图4所示，其中a为自身代价系数，b为关联代价系数。

图4 两种方案的自身代价与关联代价

2 问题描述与多目标模型

2.1 问题描述

假设企业资源计划系统(ERP系统)接收来自电子商务平台的一批订单，完成这批订单的拣选工作需搬运n个货架，控制中心基于调度算法将任务分为m组，分配至m个空闲机器人，智能仓储共有e个拣选台，每个订单由一个拣选台单独完成。单个移动机器人执行任务序列的过程中分为空载和载货两个状态[10]，两个状态下行驶的单位距离耗电量不同，耗电量与机器人的行驶距离成正比。同时考虑锂电池的放电特性[11]，电池消耗比值与剩余里程量关系如图5所示，可见随着电池使用量的增加，剩余行驶距离也在加速下降。针对不同剩余电量的移动机器人调度问题，应考虑剩余电量与任务代价的关系。

图5 电池消耗比值与剩余里程量关系图

2.2 模型符号说明

2.3 数学模型

基于“货到人”的拣选作业模式，构建多机器人的代价优化模型。模型考虑多移动机器人作业总代价最少、多移动机器人作业代价均衡两个优化目标，其目标函数如式(1)所示，F(π)取值越小，表示多移动机器人调度方案越优，其中π为一种调度方案。式(2)表示所有机器人的总任务代价，包括任务自身代价、任务关联代价。式(3)为任务代价均衡值。式(4)表示两个子目标f(π)与h(π)对总目标影响的重要程度，当w1w2时表示总代价最小为优化主要目标。式(5)为单个机器人的任务代价。式(6)为总任务代价的平均值。式(7)表示机器人空载运行代价要小于机器人载货运行代价。式(8)表示机器人电池消耗与剩余里程数之间的关系[12]。式(9)表示每个机器人的行走里程均在电量约束范围内，且有预留的安全电量返回其充电区。因剩余相同电量时，L空载>L载货，保证载货机器人能安全行驶的电量，也能保证空载机器人安全行驶相同距离，故仅考虑载货状态的剩余里程数满足安全电量要求。式(10)表示一个任务仅被一个机器人执行。式(11)表示任务全部分配至机器人。

F(π)=min(w1f(π)+w2h(π))

(1)

(2)

(3)

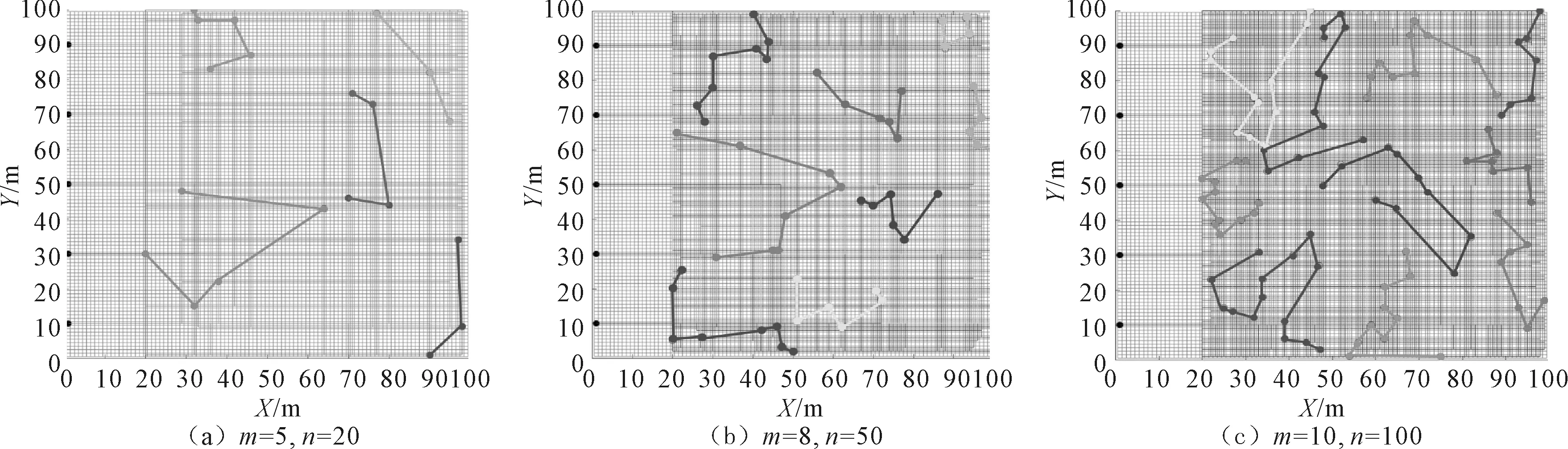
w1+w2=1,0

(4)

(5)

(6)

s.t.

θ1<θ2

(7)

L(x)=ax2+bx+c

(8)

L(1-k(r))-L(1-v)，

∀r∈{1,2,…,m}

(9)

(10)

(11)

3 面向多移动机器人协同调度的遗传算法

随着任务数量和移动机器人数量的增加，问题求解空间呈指数增长，经证明属于NP难题。针对此类问题的求解难度，遗传算法以生物进化为原型，具有很好的全局性，计算时间少，鲁棒性高，已被广泛应用于求解各类NP难题[13- 14]。故拟采用遗传算法求解多移动机器人协同调度模型。针对遗传算法在应用过程中出现的收敛慢和封闭竞争问题，将增加虚拟任务进行任务分配，快速排除不可行解，提高遗传算法的运行速度。基于虚拟任务的改进遗传算法的实现流程如图6所示。

图6 基于虚拟任务的遗传算法实现流程

3.1 初始种群与编码

在组合优化问题中，采用整数编码方式对求解问题进行直观描述。设所需完成的任务数为Ns，可调度的移动机器人数为Mr，设置虚拟任务数为Mr-1，故个体的染色体编码长度为Ns+Mr-1位。每位基因表示一个任务序号，基因的位置表示任务的执行顺序。除了第一组任务序列，其余任意两个虚拟任务之间的任务作为一个任务序列组。任务分配算法实现流程为：输入初始种群M、任务序列Ns=[Ns(1),Ns(2),…，Ns(q)]，其中q为任务的总数量，虚拟任务数组POS=[POS(1),POS(2),…,POS(k-1),POS(k),…,POS(Mr-1)]，随机分配方案，每个任务相邻位置为虚拟任务可选空位，虚拟任务数组POS表示Mr-1个虚拟任务选择的插入位置数组，Sk={NS[POS(k-1)+1],NS[POS(k-1)+2],…,NS[POS(k)]}表示插入虚拟任务后机器人k的任务序列，算法结束后输出Sk,k=1,2,…,Mr。

例如一批订单的拣选作业需搬运10个货架，即生成10个任务，可调度5辆移动机器人，增设4个虚拟任务(任务11、12、13、14)，则每个个体的编码由14个数组成。任务编码与分配方案示例如表1所示，M1～M5分别为分配后多的5组任务组。遗传算法中，将虚拟任务与实际任务之间的关联代价设置为0，将两个虚拟任务之间的关联代价设置为无穷大，则虚拟任务相邻的方案(如方案2和方案4)就会被淘汰。

表1 任务编码与分配方案示例

3.2 适应度函数

在遗传算法的运行过程中，需要通过适应度函数值来评价个体在种群中的优劣程度。个体的适应度值越大，代表个体越优秀。将适应度函数选取为：

(11)

其中，F(π)为方案π的目标函数，即方案π的总代价。

4 实验结果与分析

为了验证模型的准确性及遗传算法的有效性，采用Matlab进行仿真实验。实验设置100 m×100 m的栅格地图为实验环境，d=1 m，拣选站台的数量e=5，机器人的安全电量为总电量的10%，即v=10%可以满足机器人在仓储中的任意位置返回充电区。机器人数量m=5，每个机器人的剩余电量如表2所示。

表2 移动机器人剩余电量

随机生成待分配的任务数n=20，随机生成任务的位置与任务需到达拣选台的编号如表3所示。

表3 随机生成任务信息表

改进遗传算法的种群M=50，进化代数G=450，交叉概率Pc=0.7，变异概率Pm=0.01，初代个体编码串为随机数产生。笔者将改进遗传算法与模拟退火算法做比较，两种算法求解模型的收敛结果分别如图7和图8所示,可以看出改进遗传算法与模拟退火算法最终的适应度值相差不大，但改进遗传算法迭代至150代左右就开始收敛，比模拟退火算法的收敛效果更好。

图7 改进遗传算法收敛图

表4所示为改进遗传算法求解的任务序列、随机分配的任务序列及两种求解方法下的单个机器人代价值，其中，w1、w2均取0.5。改进遗传算法得到的调度方案中，移动机器人执行任务的代价值大幅减少，且满足电量要求。随机分配的调度方案中，单个移动机器人执行任务的代价值均较高，且3号和4号移动机器人执行任务的代价值超过了安全电量值，不符合实际工程情况。

图8 模拟退火算法收敛图

机器人编号改进遗传算法求解的任务序列随机分配的任务序列单个机器人代价值(f)改进遗传算法随机分配11-2-3-4-51-3-4-141 618.081 972.6026-7-20-85-7-10-91 260.731 624.38311-12-14-1311-6-8-201 852.702 378.08416-20-10-916-13-12-151 589.692 048.22517-18-19-1517-18-19-21 484.491 912.68

为了进一步评估模型和算法，令机器人个数分别取8、10，分别对50、100个任务进行分配。任务分配结果如图9所示，分配至同一个机器人的任务用同一连线相连，不同的机器人接收任务的结果用不同的连线区分。

投入3种不同数量机器人时，模型求解结果如表5所示，可以看出与模拟退火算法、任务随机分配方法相比，改进遗传算法优化后的各项函数值均小于模拟退火算法、随机分配方法的各项函数值，即优化后的协调调度方案在满足电量安全的情况下，有效减少了机器人执行任务代价且任务分配均衡。改进遗传算法优化函数值大多比模拟退火优化函数值更小，且改进遗传算法收敛速度优于模拟退火算法的收敛速度。故改进后的遗传算法可快速得到机器人协同调度的优化方案。

图9 任务分配结果

(m,n)算法[F,f,h]w1=0.2,w2=0.8w1=0.5,w2=0.5w1=0.8,w2=0.2m=5n=20遗传算法[7 877.92, 7 805.70, 72.22][7 877.92, 7 805.70, 72.22][7 346.79, 7 279.44, 67.35]模拟退火[8 198.32, 8 120.20, 78.20][8 301.32, 8 230.12, 71.20][8 770.21, 8 701.01, 69.20]随机分配[13 005.77 , 12 489.12 , 516.65][10 231.61, 10 057.15, 174.46][12 149.15, 11 647.10, 502.05]m=8n=50遗传算法[21 931.79, 21 855.96, 75.83][1 7661.08, 17 600.02, 61.06][20 453.15, 20 382.43, 70.71]模拟退火[22 081.43, 22 010.22, 71.21] [19 093.35, 19 013.05, 80.30][21 861.80, 21 789.61, 72.19 ]随机分配[35 497.02, 34 969.54, 527.48][28 643.21, 28 160.03, 483.18][33 124.03, 32 611.89, 512.14]m=10n=100遗传算法[46 915.45, 46 834.20, 81.25][37 779.74, 37 714.32, 65.42][43 752.41, 43 676.64, 75.77]模拟退火[47 194.68, 47 102.38, 92.30][39167.26, 39 087.46, 79.80][57 039.67, 56 958.04, 81.63]随机分配[75 478.46, 74 934.72, 543.74][60 839.18, 60 342.91, 496.27][70 409.92, 69 882.62, 527.30]

5 结论

笔者针对智能仓储环境中多移动机器人协同调度问题，构建了多移动机器人协同调度的多目标优化模型。该多目标优化模型考虑了机器人空载行驶与载货行驶的耗电差异约束条件，以及多机器人执行任务的自身代价与任务间的关联代价两个优化目标。为求解该多目标优化模型，提出了面向多移动机器人调度问题的改进遗传算法，算法通过引入虚拟任务，以构造任务分配序列。将随机分配方法、模拟退火算法与笔者的算法进行对比实验分析，结果表明，采用改进遗传算法求解文中模型可获得更好的求解结果，多移动机器人执行任务的总代价小且任务分配均衡，同时改进遗传算法的收敛性优于模拟退火算法，证明了模型的准确性及改进遗传算法在解决智能仓储多移动机器人协同调度问题的有效性。