高耸结构位移风振系数
2019-07-13钱昆
钱昆
(华东建筑设计研究院有限公司 上海200002)
引言
风振系数可分为荷载风振系数和位移风振系数,现行荷载规范采用考虑荷载风振系数的计算方法,只考虑一阶振型影响时,位移风振系数与计算点的高度位置无关,给计算带来方便。以前由位移求内力没有由外力求位移那么方便,所以规范只列出荷载风振系数,简称风振系数,但是随着有限元软件的广泛普及,由位移求内力也变得十分简单。文献[1]计算了玻璃幕墙的荷载风振系数和位移风振系数,同时引入等效位移风振系数的概念,证明了荷载风振系数与位移风振系数的内在统一性,并建议对玻璃幕墙这种结构,宜采用荷载风振系数。对于高耸结构,结构设计由结构刚度控制,按照《高耸结构设计规范》(GB50135 -2006)规定,塔顶最大位移不超过塔高的1/100,在满足这一条件下时,可以初步确定结构的高宽比,所以在高耸结构的选型设计或者初步设计时,仅需通过位移风振系数计算位移作为控制指标。本文诠释了风振系数的概念,根据随机振动理论,由位移风振系数的定义,推导出只考虑第一振型影响的表达式,引入一个参数θ,并对其进行参数分析,根据规范给出的振型公式编制出一般截面的空间相关性折算系数和参数θ的计算用表。
1 位移风振系数
工程上常将平均风响应乘以一个系数以表示平均风和脉动风共同作用的总响应,这个系数称为风振系数,等于风的总响应与平均风产生的响应之比,即:
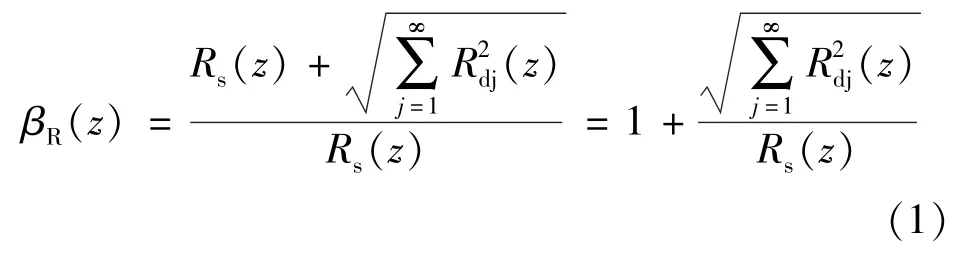
式中: R(z)、Rs(z)、Rd分别代表总响应、平均风的响应、脉动风的响应,分别代表z 高度处的位移、内力或者荷载。随着R 所表示的意义不同,而有不同的风振系数,如果把R 理解为位移,则可求出位移风振系数。
当仅考虑第一振型时,由动力学知识可得平均风位移表达式[2]为:
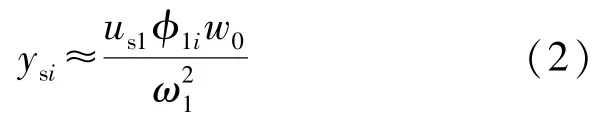
式中: us称为静力影响系数; w0为基本风压;ω1为第一振型圆频率; ϕ1i为第一振型系数。
2 高耸结构位移风振系数
由位移风振系数的定义[3],可得:

式中: βyi为位移风振系数; ydi为脉动风位移; ξ1为脉动增大系数,μ1为振型系数; m(z)为随高度变化的线质量; μs(z)、μz(z)、lx(z)、ϕ1(z)、ps(z)分别为z 高度处的风荷载体型系数、风压高度变化系数、结构宽度、第一振型系数、静力风荷载。
高耸结构仅考虑竖向相关性,可得:

式中: μf(z)为z 高度处脉动系数; ηz1为一般截面的空间相关性的折算系数; H 为结构高度; μf(z′)、μz(z′)、lx(z′)、ϕ1(z′) 分别为z′高度处的风荷载体型系数、风压高度变化系数、结构z′高度处的宽度、第一振型系数; ρz为相关性系数。
为方便应用,这里引入一个参数θ,并假定μs(z)为常数; 其表达式如下:

则式(3)可表达为:

《高耸结构设计规范》(GB50135 -2006)[4]将非等截面变化的高耸结构的体型假定为:
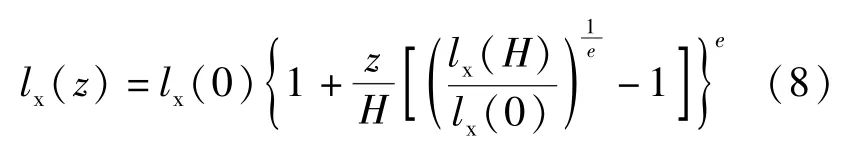
式中:e代表结构外形,e=1、e >1、e <1 分别代表结构外形为直线、内凹和外凸; lx(H)、lx(0)、lx(z)为结构顶部宽度、底部宽度、z高度处的宽度。
《建筑结构荷载规范》(GB50009 -2012)[5]将地面粗糙度分为A、B、C、D 四类,任意地貌梯度风高度HTa分别取300m、350m、450m、550m,地面粗糙度 α 分别取0.12、0.15、0.22 和0.30,故得风压高度变化系数:
由《建筑结构荷载规范》(GB50009 -2012)知脉动系数μf(z)为:
式中: g 为峰值因子,可取2.5; I(z)为z 高度处的湍流强度; I10为10m 高度名义湍流强度,对应A、B、C、D 类地面粗糙度,可分别取0.12、0.14、0.23、0.39。
Shiotami 在试验基础上,竖向相关系数ρz建议采用只与两点间距离有关的简单表达式:
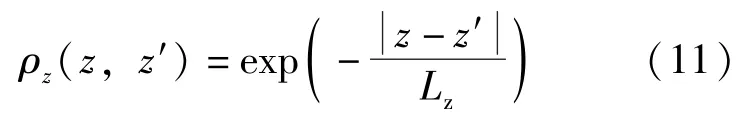
式中: ρz(z,z′)为脉动风压垂直方向的相干系数;为垂直两点间的距离。根据试验资料的统计分析可知,Lz 大部分落在40 ~60 之间,故建议取Lz =50m。对于结构的振型系数ϕ1(z),理应在结构动力分析时确定,为了简化,荷载规范在确定风荷载时,对等截面高耸结构,采用均布荷载下挠曲线为近似第1 振型,即:

3 计算分析
将式(9)的 μz(z)、式(10)的 μf(z)、式(11)的ρz和式(12)的振型公式代入式(6),采用matlab 编程,可得到ηz1随结构高度H、结构外形e、lx(H)/lx(0)和地面粗糙度的变化规律,如图1 所示。可以看出,ηz1受高度影响比较大,其他因素对其均无明显影响,将ηz1制成表格,如表1 所示。

表1 一般截面高耸结构ηz1计算用表Tab.1 Tables for calculation of tall structures with general sections
同样方法由式(7)可得到θ如图2 和表2 所示。计算表明,结构的外形e=10 时计算所得结果仅比e=0.25 时大约3%,lx(H)/lx(0) =0.1的计算结果也仅比lx(H)/lx(0) =1.0 时的计算结果大5%左右,故可忽略它们对θ的影响。式(7)的分子中多了一项脉动系数,主要由地面粗糙度决定,ηz1主要由高度决定,所以θ主要由地面粗糙度和高度决定。
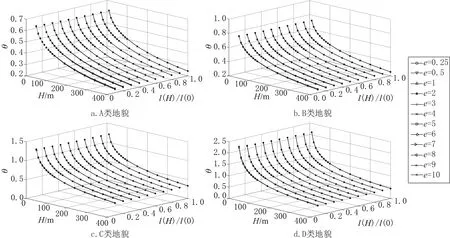
图2 系数 θ=μ1/μs1Fig.2 Coefficient θ=μ1/μs1
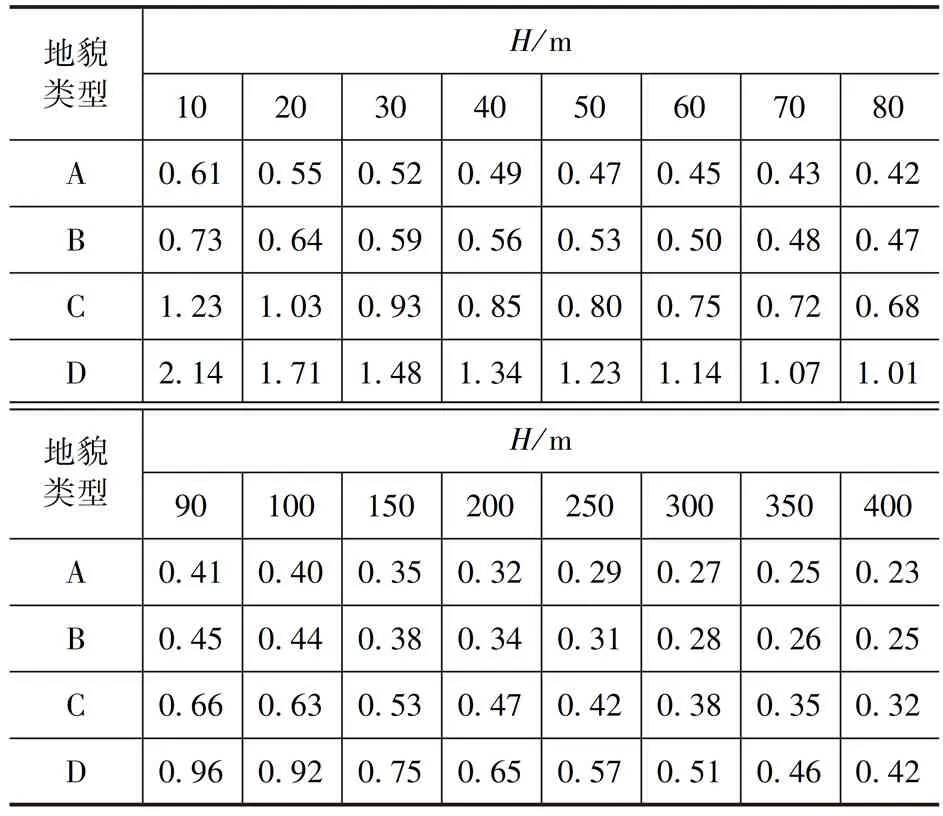
表2 一般截面高耸结构θ 计算用表Tab.2 Tables for calculating tall structures with general sections
4 结论
1.仅考虑第一振型时,根据随机振动理论,推导出高耸结构位移风振系数的一般表达式。
2.对空间相关性折算系数ηz1及参数θ进行编程分析,ηz1受高度影响比较大,结构外形e、lx(H)/lx(0)和地面粗糙度对其均无明显影响;θ主要由地面粗糙度和高度决定,结构外形e和lx(H)/lx(0)对其无明显影响。
3.将θ制成关于地面粗糙度和结构高度的表格,从而求出高耸结构位移风振系数,方便相关工程应用。
