聚乙烯燃气管道电熔接头熔区应力分析
2019-07-1244
44
(1.浙江大学 能源工程学院,杭州 310027;2.中国石油天然气管道科学研究院有限公司,河北廊坊 065000;3.浙江庆发管业科技有限公司,浙江余姚 315400;4.高压过程装备与安全教育部工程研究中心,杭州 310027)
0 引言
聚乙烯管道与传统金属管道相比具有耐腐蚀、寿命长、绝缘性好、便于运输等显著优点[1],广泛应用于城市管网。燃气管道系统作为现代城镇的重要基础设施,多分布于人口密集区域,因此管道系统的安全问题至关重要[2-3]。
管道装配现场连接过程会受到外界环境因素影响,接头质量难以保证,使焊接接头成为管道系统最薄弱的环节[4]。聚乙烯管的连接方式主要有电熔焊接、热熔焊接和机械连接。其中电熔焊接以其操作简单、易于掌握、可用于连接不同材质的管材、自动化程度较高而受人为因素和外界环境影响较小等优点,广泛应用于各种场合[5-6]。
研究表明[7],聚乙烯燃气管道失效事故中有一半以上是由于电熔接头的失效。含缺陷电熔接头主要有3种失效模式:(1)焊接界面失效;(2)电熔管件贯穿裂纹失效;(3)电阻丝界面失效[8]。其中,焊接界面失效是由于接头在内压和管道轴向力作用下,管材与管件界面剪切破坏所致。
电熔接头在服役过程中主要承受管道内压和由内压产生的轴向力。在内压作用下,管材与管件相互挤压,焊接界面受压,促使熔区闭合,不易发生失效。管道系统的轴向力在焊接界面处以切应力的形式传递,界面处产生剪切作用,切应力过大时会使界面处失效。因此轴向力是熔区长度设计时主要考虑的载荷,基于轴向力的熔区应力分析通常只考虑平均切应力。实际上,接头处轴向力不对中,管件与管材的壁厚和管径不同等因素导致切应力在界面处分布不均匀。因此,在内压与轴向力共同作用时,应力集中处成为电熔接头最危险的区域。
焊接界面上应力分布的一个重要影响因素是管件熔区长度,熔区长度的合理设置是保障电熔接头安全性的关键。目前,国内外均尚无聚乙烯管道电熔接头应力分布和熔区长度设计的相关研究,更没有相应的理论指导设计方法。
Lubkin等[9]给出了一种无限长胶接套管的理论计算方法,分析了胶层厚度、弹性模量、管材尺寸比以及搭接长度对胶接界面应力分布的影响;Goglio等[10]在此基础上进行改进,并给出公式推导过程,验证了该方法的可行性,并将模型中参数单位化,扩大此计算方法的适用范围;Troughton等[11]通过对电熔接头的拉伸试验和有限元分析,研究了接头界面应力分布情况。以上研究均发现搭接管结构界面处的切应力在搭接边缘处较大、中部较小。
关于聚乙烯燃气管道电熔管件的标准GB/T 15558.2—2005《燃气用埋地聚乙烯(PE)管道系统 第2部分:管件》中列出了不同公称直径管件所需的熔区长度最小值,但由于没有相关理论指导值可供参考,实际产品中熔区长度设计均远大于标准指导值,使得电熔管件长且制造成本高。熔区长度长,虽然焊接界面切应力较小,但是电熔管件制造成本提高;熔区长度短,虽然成本降低,但焊接界面切应力增加,接头容易发生强度失效。合理的熔区长度是电熔管件强度裕量和经济成本的均衡点。电熔接头焊接界面应力分布的准确分析是接头熔区长度设计的基础。
本文通过理论计算和有限元模拟两个方面,研究不同管道结构时聚乙烯电熔接头的受力情况,得到接头焊接界面的应力分布,探究实际焊接界面处切应力最大值与Mises应力最大值随熔区长度的变化规律。
1 理论模型计算
1.1 电熔接头轴向力的影响因素
聚乙烯管道电熔接头在服役过程中受到内压与轴向力的共同作用,内压为管道工作压力,轴向力的大小及产生的原因与接头附近管道的结构有关。如果接头附近有端盖或弯头,内压会使电熔接头处产生轴向封头力;如果管道长且直,则管材轴向应变为零,即平面应变情况[12],同时,当温度变化时会产生轴向温度应力。聚乙烯管电熔接头的结构如图1所示。
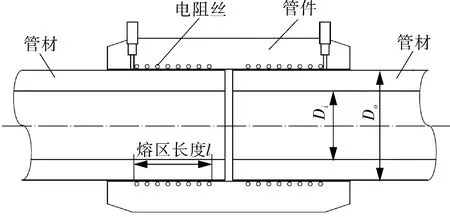
图1 电熔接头结构示意
(1)接头附近有端盖或弯头。
管廊内排布的聚乙烯管道有一定的活动空间,当接头附近弯头较多或有端盖时,内压会使得接头处产生轴向封头力。由于管道沿轴向可以发生变形,所以当温度变化时接头处不会产生温度应力。对于这种情况,只需要分析封头力在电熔接头焊接界面上产生的切应力。
内压产生的封头力为:
(1)
式中F1——内压产生的封头力,N;
P——管道工作压力,Pa;
Di——管材内径,m。
轴向封头力F1在焊接界面上产生的平均切应力为:
(2)
式中τm1——轴向封头力在焊接界面上产生的平均切应力,Pa;
Do——管材外径,m;
l——管材与管件连接处的熔区长度,m。
(2)接头两边为无限长管道。
埋地聚乙烯管大多为长直管,土壤会约束管道的活动范围,为平面应变情况。内压作用下,管道轴向应变为零,轴向应力为:
(3)
式中σz2——内压作用下管道的轴向应力,Pa;
μ——泊松比。
由于管道轴向应变为零,当温度变化时,管道会产生轴向温度应力。与管材安装闭合时的环境温度相比,当温度变化ΔT时,由GB 50253—2014《输油管道工程设计规范》,无限长管道的轴向力为:
(4)
式中F2——无限长管道在内压和温度变化作用下的轴向力,N;
α——线胀系数,℃-1;
E——弹性模量,Pa。
考虑温度变化影响的无限长直管道电熔接头焊接界面上的平均切应力为:
(5)
式中τm2——无限长管道在内压和温度变化作用下的轴向应力,N。
1.2 电熔接头焊接界面理论公式推导
本文以Lubkin模型[9]为基础,构建了电熔接头焊接界面应力理论计算模型,如图2所示。管道工作压力为P,接头处轴向力为F。取两管材交界面(即管件中心处)为轴向x坐标原点。管材与管件的厚度分别为t1,t2;中径分别为a1,a2;弹性模量分别为E1,E2;泊松比分别为μ1,μ2;管材内半径为a0。管件与管材焊接处的熔区厚度为η;中径为a;弹性模量为Ea;剪切模量为Ga;管材与管件焊接处熔区长度为l。
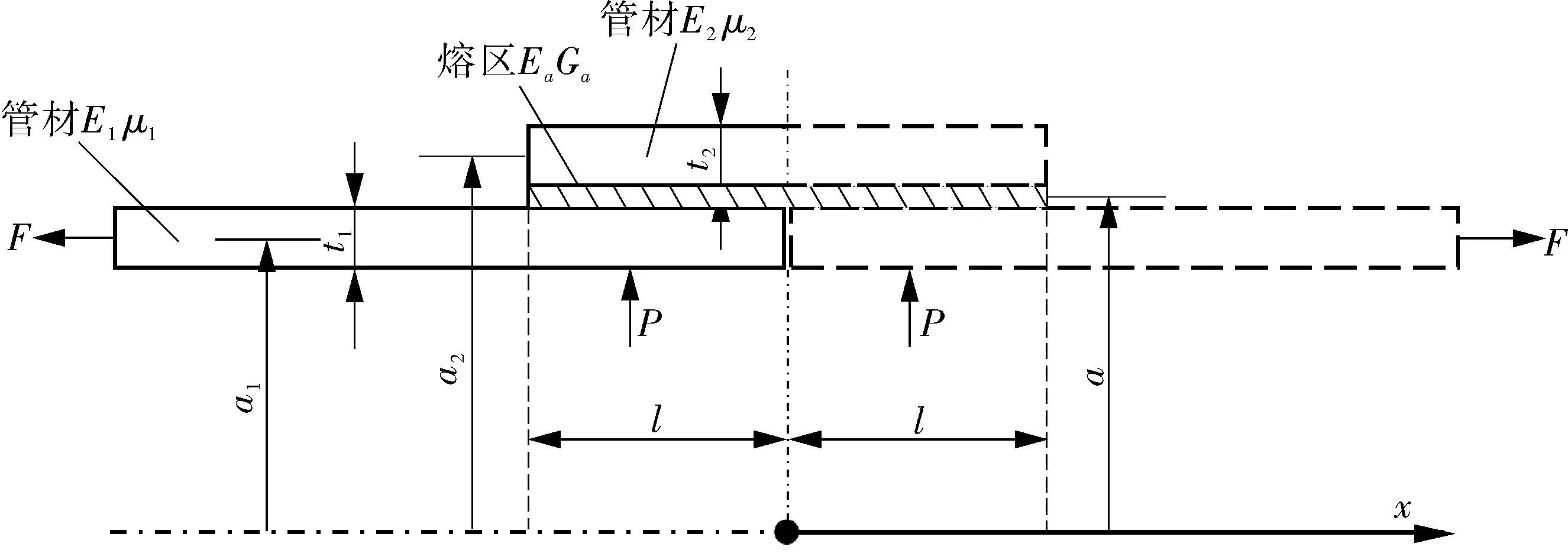
图2 电熔接头理论计算模型示意
电熔接头服役时受内压载荷与轴向载荷共同作用。管材与管件都是薄壁管,推导过程中采用薄壳理论。熔区与管材壁厚相比非常薄,因此,假设熔区内正应力与切应力沿厚度方向保持一致;假设弯曲变形很小,计算中不考虑几何非线性影响。


图3 电熔接头管材与管件微元受力分析示意
对微元进行受力分析,可以得到平衡微分方程:
(6)
(7)
(8)
(9)
(10)
对管材和管件分别列轴向与环向的物理方程以及挠曲线近似微分方程:
(11)
(12)
(13)
对熔区列几何方程,正应力和切应力分别满足以下方程:
(14)
(15)

(16)
(17)
(18)
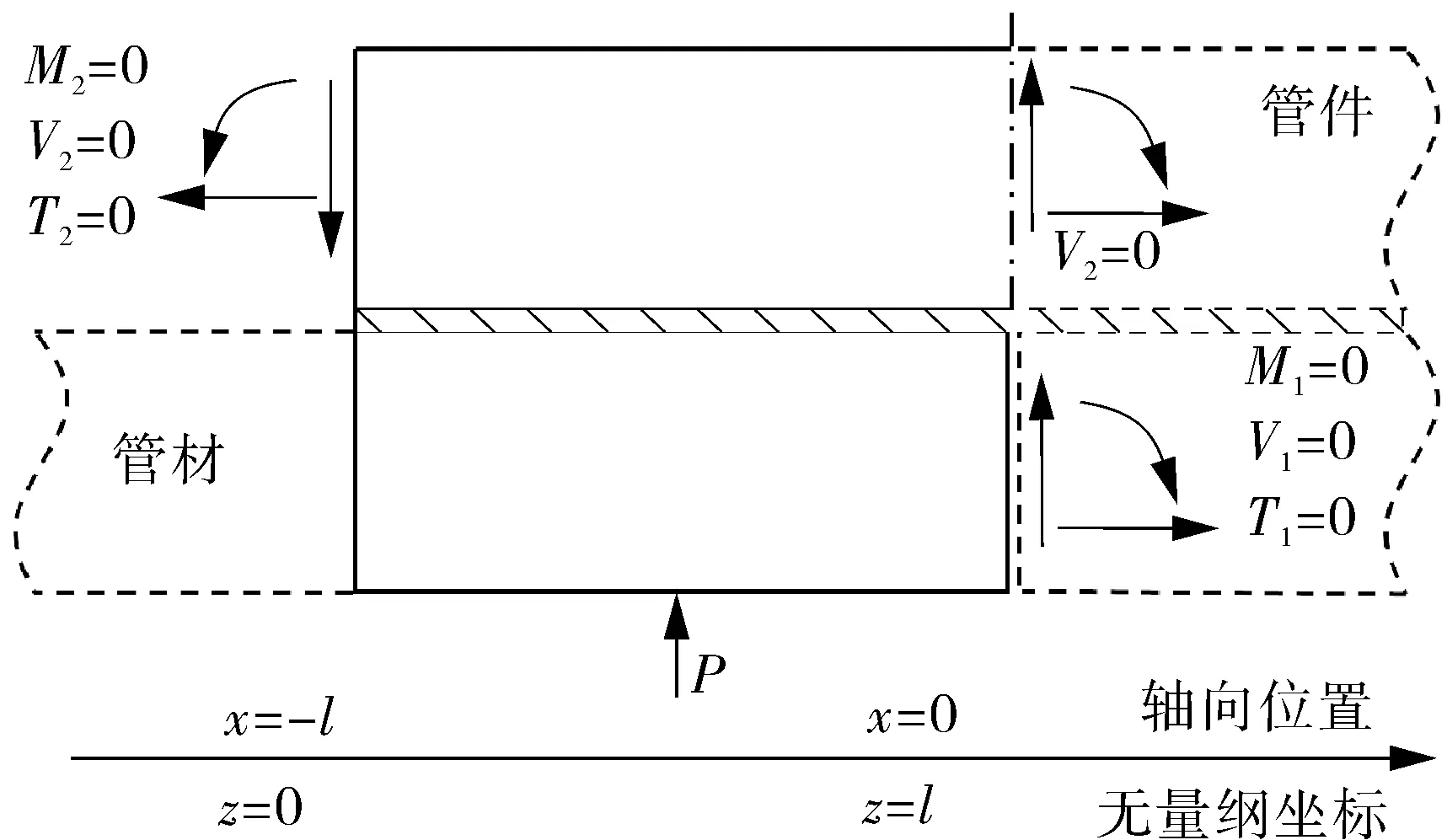
图4 电熔接头模型边界条件示意
式(16)~(18)为2个四阶微分方程与1个二阶微分方程,需要10个边界条件可求得唯一解。对于管材与管件单侧焊接部分,管件外侧、管材内侧和熔区两侧边缘处均为自由边界,如图4所示。
自由边界处的应力与力矩均为零,即:
(19)
接头结构关于管件中心处(x=0处)横截面对称,所以应力分布关于x=0处横截面也对称,管件在对称截面处的切应力与挠度的导数均为0,即:
(20)
根据变形连续性条件,管件与管材焊接区域的挠度与转角一致,结合管件无限长假设,可以得到:
(21)
其中:
式(19)~(21)提供了10个边界条件,此模型有唯一解。结合文献[9-10]中的计算方法,求解方程(16)~(18),可得到电熔接头焊接界面上应力大小。
计算过程中,令F=F1,可以得到电熔接头附近有端盖或弯头的情况下,轴向力与封头力共同作用在接头处时,焊接界面上的应力分布;令F=F2,可以得到接头两边为无限长管道的情况下,内压与温度变化在电熔接头焊接界面上的应力分布。
1.3 电熔接头有限元模型分析
以公称外径dn=110 mm,管材标准尺寸比为SDR11,材料PE100的聚乙烯燃气管为例,计算电熔接头焊接界面的应力分布。GB/T 15558.2—2005中规定,聚乙烯电熔管件材料与所连接的管材为相同最小要求强度(MRS)分级的聚乙烯材料时,管件的壁厚应大于等于管材最小壁厚。为了简化计算,取管件与管材壁厚相等,有限元模型的尺寸参数如表1所示。管材与管件使用高密度聚乙烯材料,燃气管道工作压力较低,认为材料处于线弹性范围内。材料参数取聚乙烯长时弹性模量E=400 MPa,泊松比μ=0.45[13]。熔区及附近网格尺寸为0.25 mm,如图5所示,管材施加内压载荷P,管材中心截面设置对称约束,管材外边缘横截面施加轴向载荷F。
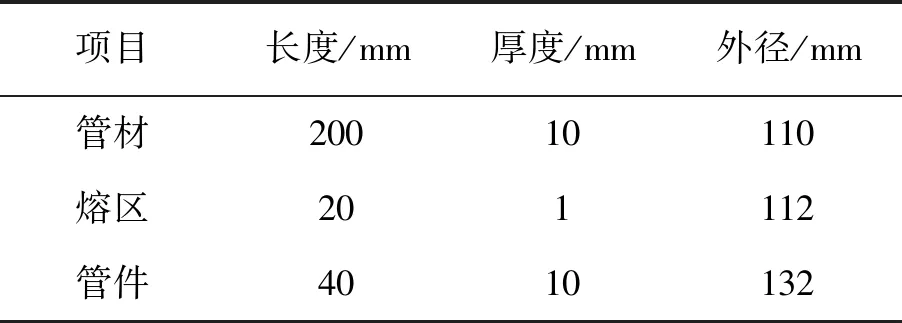
表1 有限元模型几何尺寸

图5 电熔接头有限元模型尺寸及网格划分示意
载荷P取管道最大工作压力,根据CJJ 63—2018《聚乙烯燃气管道工程技术标准》,聚乙烯燃气管道的最大工作压力(MOP)为:
(22)
式中MRS——最小要求强度,MPa,对于PE100材料,取MRS=10 MPa;
C——设计系数,燃气管取C=2.5;
SDR——标准尺寸比,即管材公称外径与公称壁厚的比值。
因此,模型内压载荷P=0.8 MPa。
载荷F为接头受到的轴向力,根据管道结构分为两种情况:
(1)当接头附近有端盖或弯头时,轴向力F=F1=5 089 N。
(2)当接头两边为无限长管道时为平面应变情况。一个地区一年内季节更替导致埋地管道处土壤的温度变化范围一般不超过20 ℃[14-17],计算温度应力最大的情况,假设管道在夏季埋入,冬季时产生的温度应力最大,取ΔT=-20 ℃,聚乙烯线胀系数α=1.5×10-4℃-1,泊松效应和温度变化共同引起的轴向力F=F2=8 916 N。
上述情况(1)中轴向载荷为管道服役过程中基本稳定不变的载荷,情况(2)中轴向载荷随季节周期性变化。对电熔接头有限元模型施加两种载荷,可以分别计算出两种管道结构接头焊接界面上的应力分布情况。
1.4 模型计算结果

取有限元计算结果的熔区中径处切应力作为界面切应力;将具体尺寸与材料参数代入第1.2节中的理论公式,可解得理论公式法的界面切应力。将理论公式法与有限元法的界面切应力做对比,两种方法计算出的两种轴向力条件下切应力结果如图7所示。理论公式和有限元两种方法计算得到的切应力沿轴向分布曲线均呈两边大、中间小的“U形”规律,切应力最大值出现在z=1处,即熔区内边缘处,两条曲线在两端边缘附近差别较大,中部比较吻合。
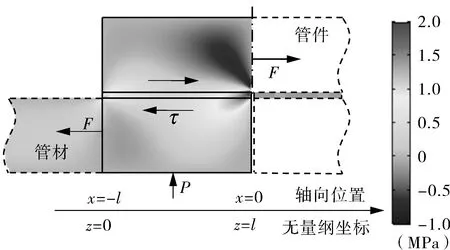
图6 电熔接头有限元模型切应力分布

(a)轴向力为封头力计算结果(F=F1)

(b)平面应变情况轴向力计算结果(F=F2)图7 理论计算与有限元计算的焊接界面相对切应力
熔区内外边缘处(z=0和z=1)为自由边界,表面切应力为零。由切应力互等定理,焊接界面上切应力在自由边界处(z=0和z=1)也为零,图7中有限元模型得到的切应力分布曲线两端突然减小至零,符合真实情况。本文第1.2节中理论公式计算的基本假设认为,熔区厚度与管材壁厚相比非常薄,熔区内切应力沿厚度方向保持一致,即熔区处应力分布不随径向变化。这一假设把熔区在z=0和z=1处的边界条件设置为非自由端,使得理论简化模型结果与实际情况有偏差,即理论公式计算出的熔区切应力在边缘处是不准确的。此外,理论公式推导中不考虑几何非线性的影响,也导致计算结果与有限元结果有差别。
因此,与理论公式法相比,有限元法计算出的电熔接头焊接界面切应力分布结果更接近真实情况。两种方法在远离边缘处区域计算结果较吻合,说明了有限元模型的合理性。本文第2部分将采用有限元方法进行分析,几何模型采用图1所示的结构。
焊接界面上平均切应力τm为轴向力与焊接面积的比值。当轴向力为封头力时,由式(2),τm=τm1=0.74 MPa;当轴向力为平面应变情况产生的轴向力时,由式(5)算得,τm=τm2=1.29 MPa。观察图7中焊接界面切应力相对值可知,切应力分布非常不均匀,尤其是在焊接界面边缘,数值明显大于平均切应力。为了定量表示焊接界面切应力分布不均匀程度,定义端部切应力集中系数k为最大切应力与平均切应力之比,即k=τmax/τm。图7中,有限元法计算得到两种情况轴向力对应的k分别为2.69和2.68,差别小于0.5%。两种不同轴向力情况的计算结果曲线形状相同,说明对于相同的电熔接头结构,轴向力对界面切应力的相对分布规律影响较小,主要影响界面切应力整体值,因此,下文对于界面应力相对分布规律的分析,仅考虑轴向力为封头力的情况。
2 电熔接头应力分布与熔区长度规律
2.1 切应力分布与熔区长度规律
保持有限元模型其他参数不变,改变熔区长度值,计算焊接界面上的切应力最大值和端部切应力集中系数k,其结果见图8。熔区长度越长,焊接面积越大,焊接界面上的平均切应力越小,切应力最大值越小,k值越大。k是反映界面切应力分布不均匀性的指标,k越大,应力分布越不均匀,承载切应力的部分主要为熔区两端边缘附近材料,熔区中间部分处于低应力状态,材料利用率较低。但是k较小时对应熔区长度较短,可能使接头无法满足强度要求。因此,熔区长度是聚乙烯管电熔接头焊接界面应力分布的重要影响因素。
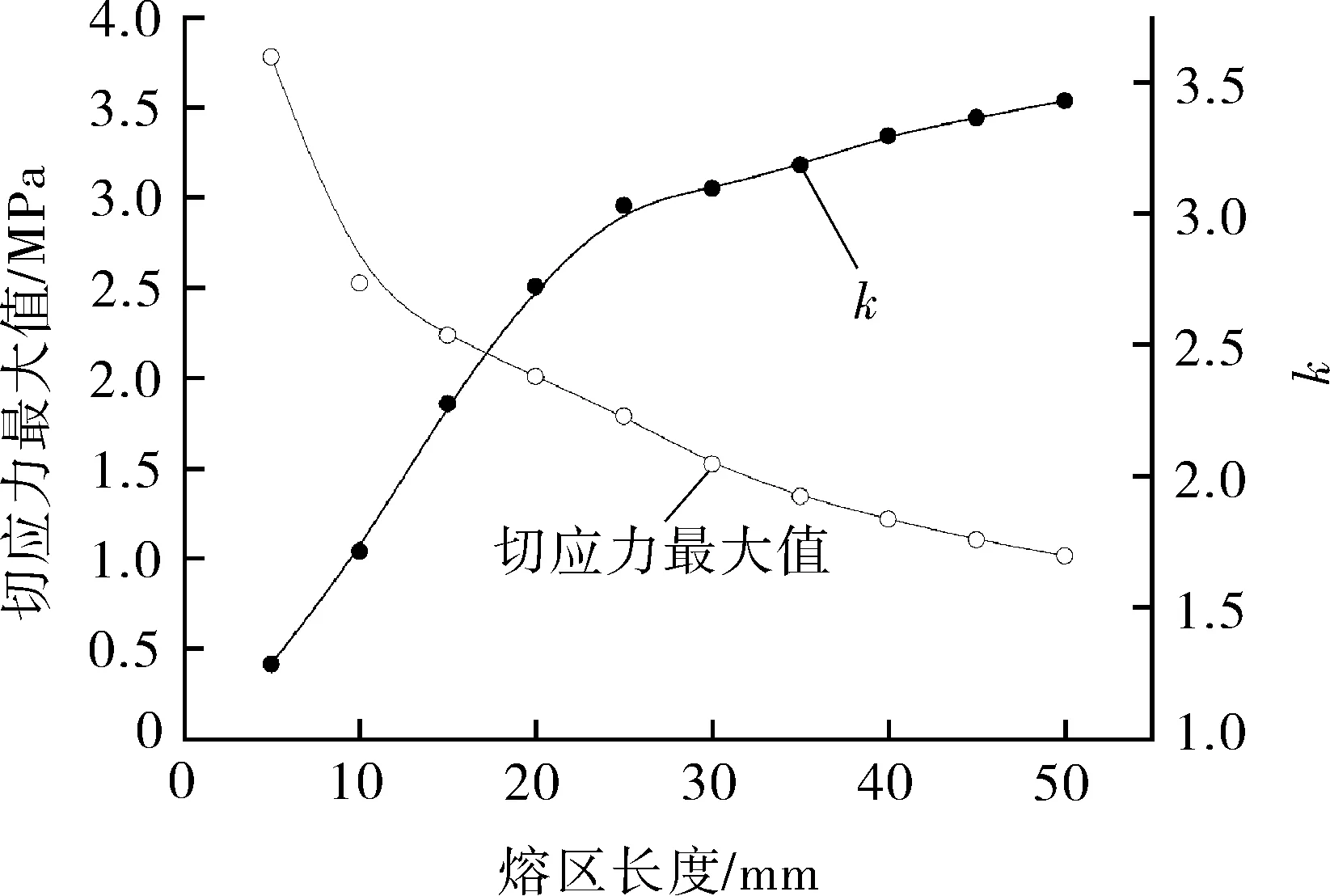
图8 切应力最大值和端部切应力集中系数k随熔区长度变化关系
2.2 Mises应力分布与熔区长度规律
聚乙烯电熔接头实际结构在熔区两侧存在内外冷焊区,内冷焊区会使接头焊接界面上的应力分布不均匀程度加剧;外冷焊区对界面应力分布影响较小。对有限元模型增加内冷焊区结构,计算焊接界面上的应力分布,仍呈两边大、中间小的“U形”规律,但端部应力值增加。由存在冷焊区的模型计算Mises应力与切应力,分布规律相似,图9(a)示出不同熔区长度时焊接界面上的Mises应力和切应力。当管材与管件尺寸一定、管道系统工作压力一定时,接头焊接界面上切应力最大值与Mises应力最大值均随熔区长度的增加而减小,切应力最大处与Mises应力最大处基本重合。电熔接头焊接界面上,环向切应力为零,径向力和环向力与轴向力相比较小,界面上主要受内压与轴向切应力。电熔接头结构在轴向力与内压共同作用在下,焊接界面边缘产生应力集中,Mises应力在熔区与内冷焊区交界处附近达到最大。类似地,定义端部应力集中系数Mk为焊接界面上Mises应力最大值与平均切应力之比,Mk与熔区长度有关。
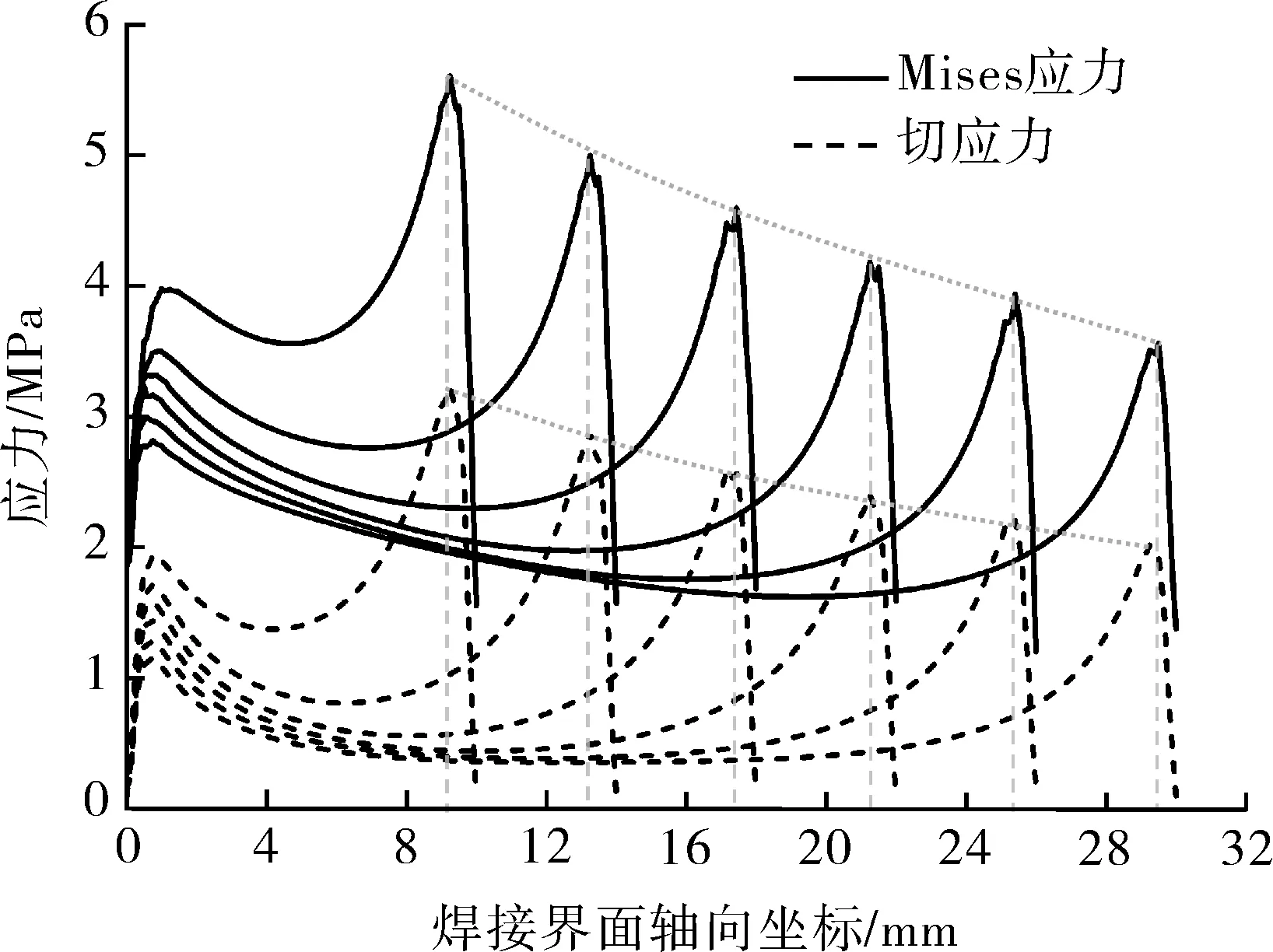
(a)

(b)图9 不同熔区长度应力分布与应力集中系数
端部应力集中系数Mk与切应力集中系数k随熔区长度的变化规律见图9(b)。Mk表征了电熔接头焊接界面上Mises应力的相对值,反映了焊接界面上应力分布不均匀程度。随着熔区长度的增加,Mk增加,并且Mk与熔区长度近似呈线性关系。熔区长度越长,电熔接头的强度越高,但是Mk越大,界面应力分布越不均匀,主要承载应力区域集中在熔区边缘处,材料的利用率降低。
2.3 不同管材规格电熔接头端部应力集中系数
目前,标准聚乙烯燃气管道主要使用PE80与PE100两种材料,管材标准尺寸比主要有SDR11和SDR17两种。计算不同材料、不同SDR、不同管径的管材在不同熔区长度时的端部应力集中系数Mk,绘制Mk随熔区长度变化图,发现不同规格电熔接头计算结果落在一条直线附近,如图10所示。说明Mk受管径、管材尺寸比和材料的影响较小,故焊接界面应力分布不均匀程度的主要影响因素为熔区长度。由最小二乘法拟合得到端部应力集中系数Mk与熔区长度l之间的函数关系:Mk=0.13l+2.79(其中,l的单位为mm,Mk为无量纲数)。
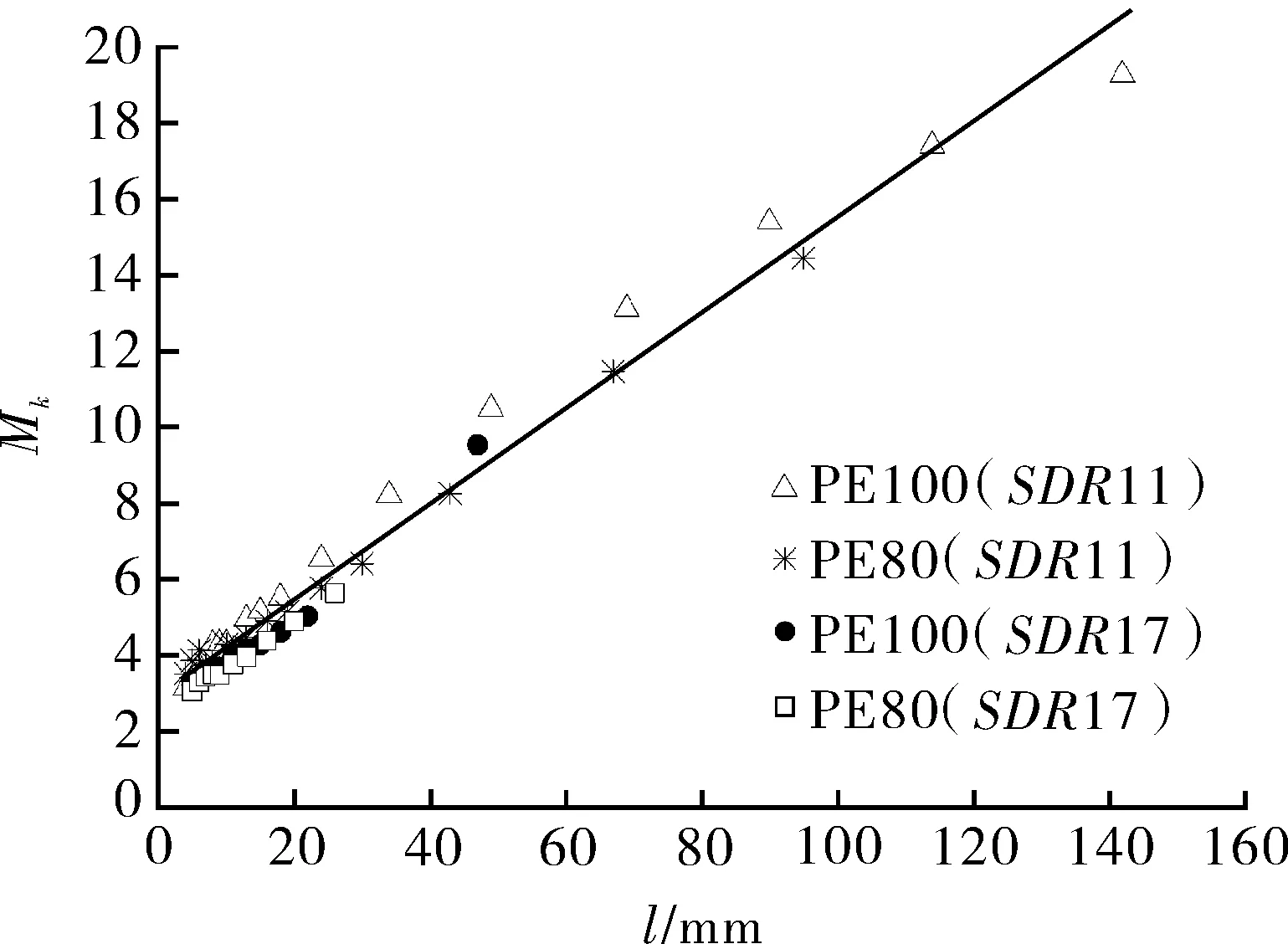
图10 端部应力集中系数与熔区长度的关系
由已知工作压力和管材尺寸等条件可以计算出聚乙烯管电熔接头焊接界面上的平均切应力,平均切应力与拟合函数Mk相乘可以计算出最大Mises应力,令最大Mises应力等于许用应力,即可解得满足电熔接头强度的最小熔区长度。本文方法可以计算不同载荷工况、不同管径的PE80和PE100电熔接头端部应力集中系数,为电熔接头熔区长度设计提供理论依据支撑,也可为核电等相关应用领域电熔接头设计[18]提供快速计算方法。
3 结论
(1)聚乙烯管电熔接头结构在内压与轴向力作用下,界面应力分布不均匀,切应力与Mises应力沿轴向为两边大、中间小的“U形”分布,在熔区与内冷焊区交界处附近达到最大值,切应力最大值的位置与Mises应力最大值的位置基本重合。
(2)电熔接头焊接界面上切应力分布不均匀程度主要与熔区长度有关,受轴向力大小、管径、管材尺寸比、材料等因素影响较小。
(3)电熔接头焊接界面的应力集中系数Mk随熔区长度l呈线性变化规律,其近似关系为Mk=0.13l+2.79,该式可为不同载荷工况、不同管径的电熔接头熔区长度设计提供快速计算方法。
