多重复合油藏探测半径计算与地层压力分布

邓 琪 张宏友 汪全林 谭 捷 靳心伟

中海石油(中国)有限公司天津分公司, 天津 300452

0 前言

某个时刻压力波在地层中传播的最大径向距离称作油井的探测半径[1]。探测半径是确认储层变化边界与井控储量的重要参数,研究不同时刻地层压力分布与探测半径,对于正确评价油藏具有十分重要的意义[2-14]。目前采用的主流软件在求取径向复合油藏探测半径时,没有考虑储层物性的变化,导致了计算结果不可靠。对于复合油藏中的压力变化,尹洪军、万贵春、李顺初等人[15-17]利用Stehfest数值反演方法分析了复合油藏的压力变化并得到了相应的数值解。对于复合油藏的探测半径,王新海等人[18]通过物质平衡方程研究了双重复合油藏调查半径与表皮系数,崔迪生[19]和李传亮等人[20]分别利用试凑法和增量法推导了不同的探测半径计算式。以上研究均未提出多重径向复合油藏的探测半径与地层压力分布解析计算式。

本文从直井不稳定渗流的数学模型出发,分析了径向复合油藏的压力分布特点,提出了虚拟探测半径的概念,并以此为基础得到了双重及多重径向复合油藏的探测半径与地层压力分布解析计算公式。

1 双重径向复合地层

当压力波未传播到储层物性变化边界时,压力波传播特点与在均质无限大地层时一致,此时平面径向流数学模型为:

(1)

导压系数计算式:

(2)

式中:pi为原始地层压力,MPa;t为生产时间,ks;h为储层厚度,m;r为径向距离,m;q为产量,m3/ks;K1为储层渗透率,μm2;φ为孔隙度,f;μ为地层流体黏度,mPa·s;Ct为综合压缩系数,MPa-1。

由式(1)可得不稳定渗流的压力解为:

(3)

相应的无限大地层平面径向流的探测半径计算公式可表示为[3]:

(4)

式中:β为常数。

为了更方便地理解探测半径随时间t的变化关系,将式(4)两边取平方,并对t求导可得[20]:

(5)

式(5)表明当储层物性一定时,探测半径的平方与测试时间呈线性关系,其中斜率为β2η1。

当储层物性发生变化时,可将储层简化为内圈和外圈,导压系数分别为η1和η2,内圈半径为r1。假设内圈与外圈的孔隙度与综合压缩系数变化不大,由式(1)可得,内外圈的流度比为:

(6)

到达外圈后,探测半径随时间的变化关系为:

(7)

假设此时外圈的物性与内圈相同,对应的虚拟探测半径为ri1,仍采用式(4)计算。联合式(4)与式(7)可得:

(8)

由式(8)可知,由于储层物性的变化,导致同一时刻探测半径平方的变化量变为均质储层情况下的1/M倍,对式(8)积分可得实际探测半径ri与虚拟探测半径ri1的关系式为:

(9)

进而可得不同流度比下的探测半径计算公式为:

(10)

由式(10)求得,某一时刻不同内圈半径、不同流度比下的探测半径变化曲线见图1。

图1 不同内圈半径下探测半径随流度比变化曲线

从图1可以看出:总体上随着流度比的增加,探测半径逐渐降低,且降低的幅度越来越小;当流度比小于1时,随流度比的增加,探测半径迅速下降;当流度比大于1时,探测半径随内圈半径的增加而增加。

由文献[3]可知,式(3)可近似表达为:

(11)

式中:γ为常数1.781。

式(11)进行微分变换可得:

(12)

由式(12)可知,不稳定径向流时,半对数坐标下,在探测半径内某一时刻某一位置处的地层压力,与单位时间径向距离的平方呈线性关系。对式(12)进行分段积分,得到双重径向复合下当ri>r1时,地层压力解析表达式为:

由式(13)求得,某一时刻不同流度比下的探测半径变化曲线见图2。

从图2可以看出,当第二圈储层变好时(M=0.6),压降漏斗变化更平缓,对应的探测半径越大,反之当第二圈储层变差时(M=2),压降漏斗变化更剧烈,对应的探测半径越小。

图2 不同流度比下双重径向复合地层压力分布图

2 多重径向复合地层

当地层为n重复合时,根据双重径向复合研究成果,每一次储层物性变化的影响,都导致压力的变化量被拉伸(或压缩),由水电相似原理,得到当ri>rn-1时,n重径向复合地层的地层压力分布式为式(14)。此时,设第n圈储层的渗透率变化为上一圈的1/Mn-1倍,可得n重径向复合地层的探测半径计算式为式(15)。

(14)

(15)

以n等于3为例,由式(14)计算求得r1=50 m,r2=100 m时某一时刻不同流度比下的地层压力分布曲线，见图3。

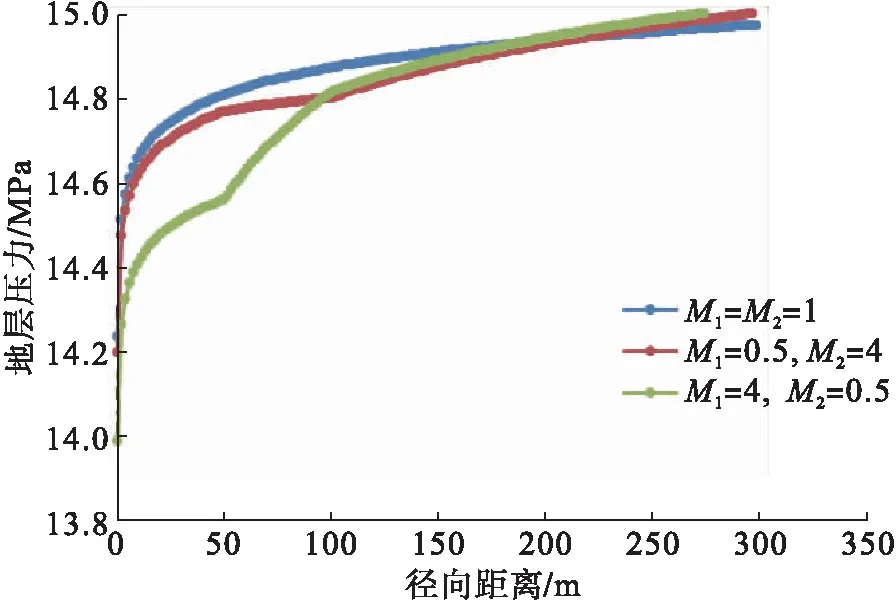
图3 不同流度比下三重径向复合地层压力分布图

从图3可以看出,总体上随储层物性的变化,地层压力呈现出不同的分布曲线。特别是,当第二圈流度变为第一圈流度的2倍时(M1=0.5),由于储层物性变好,同均质储层(M1=M2=1)相比,此时第二圈流度的压力损耗减少。当第三圈流度变为第二圈流度的0.25倍时(M2=4),由于储层物性变差,此时第三圈的压力损耗增加。

3 实例应用

以渤海油田评价井A1井为例,该井测试层位地层原油黏度0.63 mPa·s,产层厚度31.2 m,测试产量290 m3/d。图4为该井关井压恢的双对数曲线。根据相关认识,采用径向复合模型进行试井解释,拟合情况见图4。

由图4可知,该井外圈储层物性变好,压力传导能力增强。由软件直接得到的探测半径为126 m,利用本文方法计算得到的探测半径为265 m。目前的地质认识表明,本区块近井350 m以内为落实的储层区域,因此新方法分析结果与静态认识具有较好的一致性。

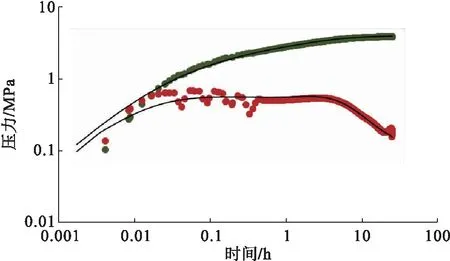
图4 A1井关井压恢试井曲线

4 结论

1)针对径向复合地层的实际情况,提出了虚拟探测半径校正法,进而推导了多重径向复合地层探测半径与地层压力分布解析计算式。

2)研究表明随着流度比增加,探测半径逐渐降低,且降低幅度越来越小;当流度比小于1时,复合地层探测半径随流度比增加迅速降低。

3)实例应用表明本文方法简单可靠,更能准确描述径向复合油藏的探测半径变化特点。