基于动态平差与静态平差的水准监测网精度分析与研究

赵新华 孙江涛 曹继如

【摘 要】论文采用动态平差与静态平差的方法对某水准监测网进行数据处理，解算两种不同平差方法下水准点高程的变化量及变化速率，认为在一些长期周期性的水准监测网中采用动态平差方法可以较为准确地表达监测点的变形信息。

【Abstract】This paper uses the method of dynamic adjustment and static adjustment to carry on the data processing to a certain level monitoring network， calculates the change amount and change rate of the leveling point elevation of two different adjustment methods， and thinks that the deformation information of monitoring points can be expressed more accurately by using the method of dynamic adjustment in some long-term periodic level monitoring networks.

【关键词】水准监测网;动态平差;静态平差;高程速率

【Keywords】 leveling monitoring network; dynamic adjustment; static adjustment; elevation rate

【中圖分类号】P624                                          【文献标志码】A                                【文章编号】1673-1069（2019）05-0161-02

1 引言

在常规的水准测量中，在进行数据处理前往往要首先确定水准网的位置基准信息[1]，然而对于一些精密工程测量中，如大型桥梁施工[2]、大型精密设备安装[3]等工程测量中为获取网中各个点位随时间变化的信息，在平差计算时，一般不需要提供位置基准信息。本文分别采用不设起算点的动态平差与静态平差两种方法，对某水准网中监测点的动态变化信息进行平差计算，并对比分析两种方法各自在体现点位位置随时间而发生变化的精度。

2 平差模型原理及其公式

2.1 动态平差

经过平差解算后，其单位权中误差为：

其中n为高差观测值总个数。

最后，求得各水准点高程及其速率中误差为：

2.2 静态平差

静态平差模型的计算公式主要如下所示[5]，其误差方程

为：V=BX+l（9）

平差模型的法方程为：NX+W=0（10）

式中，N=BTPB，W=BTPl。

因此，未知数X的解为：X=-N-1W（11）

协因数矩阵为：Qx=N-1（12）

3 案例分析与结果

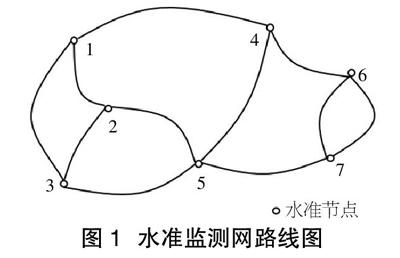
采用某一动态水准网分别采用动态平差和静态平差方法进行观测值数据处理，依据以上两种平差原理及公式进行解算，求得各水准点的变化量及其变化速率，并对计算结果进行对比分析。如图1所示为某水准路线图，该水准网中共有7个未知点，依据项目作业计划，对该水准网的不同时段开展了三次作业观测。

表2为动态平差方法与静态平差方法的水准网解算结果，从表中可以看出，两种平差模型的精度差异较大，其中动态平差模型解算的高程中误差分布较为随机，没有误差累积或者传递现象，然而静态平差模型的精度受到了很大影响，其中距离水准网的起算点也就是1号点越远，其高程中误差越大，说明点位精度越低，这说明静态水准测量在遇到基准点同步发生位置信息变形时，其不能精确地表示出水准点的变化规律。

4 结论

本文通过对某水准监测网进行实例分析，分别采用动态平差和静态平差的方法进行平差计算分析，获取了不同周期水准点的变形信息及高程变化速率，对结果进行分析后主要得出以下结论：

①采用静态平差方法进行数据处理时，如果基准点位置信息发生了变化，则不能准确表示出其他水准点的位置变化信息，同时也无法准确体现出水准网中各个水准点随时间改变的高程速率变化信息。

②两种平差方法进行比较，采用动态平差方法解算出的高程误差信息没有出现误差累积或传递现象，然而静态平差方法则影响较大，且结果显示，水准点距离基准点越远，高程中误差越大，点位精度越低，静态水准测量在遇到基准点同步发生位置信息变形时，其不能精确地表示出水准点的变化规律。

【参考文献】

【1】曾祥新，邱蕾，王泽民.南宁市二等水准网的数据处理与精度分析[J].地理空间信息，2011，09（2）：21-22.

【2】吴迪军，熊金海，熊伟.大型桥梁施工测量监控与管理方法研究[J].工程勘察，2012，40（1）：66-68.

【3】樊文静.高精度GPS数据处理及整周模糊度搜索算法的研究[D].西安：长安大学，2011.

【4】刘根友，郝晓光，柳林涛.参数约束平差法[J].大地测量与地球动力学，2006，26（4）：5-9.

【5】於宗俦.测量平差基础[M].北京：测绘出版社，1982.