柔性基、柔性关节空间机械臂的运动混合控制
2019-07-11陈志勇张婷婷
陈志勇 张婷婷
福州大学机械工程及自动化学院,福州,350116
0 引言
空间机械臂适于执行空间平台搭建、捕获大型目标物体等任务,其研究一直是人们关注的焦点[1-4]。因制造、技术等客观原因,现实中的空间机械臂各主要部件均具有一定的柔性,这些柔性不可避免地对系统的操作运动产生负面影响,如降低系统控制精度,影响系统稳定性。近年来,为提高空间机械臂的实时操控精度,人们除对空间机械臂的臂杆柔性问题进行研究外[5-7],还研究以往极易被忽视的关节柔性、基座柔性。如文献[8]提出一种柔性关节空间机械臂末端跟踪的反馈线性化控制策略;文献[9]研究了本体无控参数确定柔性关节空间机械臂在关节及工作空间下的控制问题;文献[10]讨论了外部扰动及参数不确定影响下,柔性关节空间机械臂的动力学建模与双时间尺度鲁棒控制问题;文献[11]探讨了一种自由漂浮柔性基机器人的零空间反应控制问题;文献[12]设计了一种柔性基空间机械臂自主目标捕获的速度分解控制算法。上述研究仅限于解决关节或基座主导柔性影响的空间机械臂主动控制问题。显而易见,若同时考虑基座和关节的柔性,则空间机械臂的动力学模型将变得更为复杂,控制难度更大[13-14]。现有探讨各类不确定性影响下柔性基、柔性关节空间机械臂末端运动控制问题的研究还尚不多见,且亟待更进一步地积累与完善。
本文旨在解决参数不确定、外部扰动并存的柔性基、柔性关节空间机械臂基座姿态与末端负载的轨迹追踪控制、基座与关节柔性振动的主动抑制问题。首先,依据奇异摄动分解技术及系统运动学关系,将系统动力学模型降阶为一个表征系统刚性运动的增广惯性空间慢变子系统、一个表征系统双柔性振动的快变子系统。其次,为消除系统不确定性的影响,针对增广惯性空间慢变子系统,提出一种基座姿态与末端负载协调运动,且基于等效控制、鲁棒控制、参数自适应调整算法的自适应鲁棒终端滑模控制律。为抑制柔性基及柔性关节在运动过程中的柔性振动,针对快变子系统设计了一种基于自适应观测的最优控制策略。仿真结果验证了所提方案在消除系统不确定性影响,抑制基座与关节柔性振动,实现系统预期轨迹跟踪控制上的有效性。
1 动力学模型的描述及分解
以图1所示柔性基、柔性关节平面两杆空间机械臂为例进行研究。据文献[14]并综合考虑系统存在外部扰动的情况,建立修正后的系统操作臂动力学子方程:
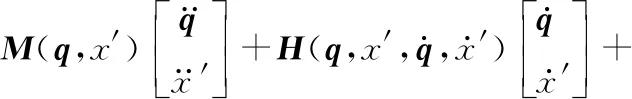
(1)
及相应的驱动电机动力学子方程:
Jmθm+kmσ=τm
(2)
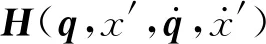
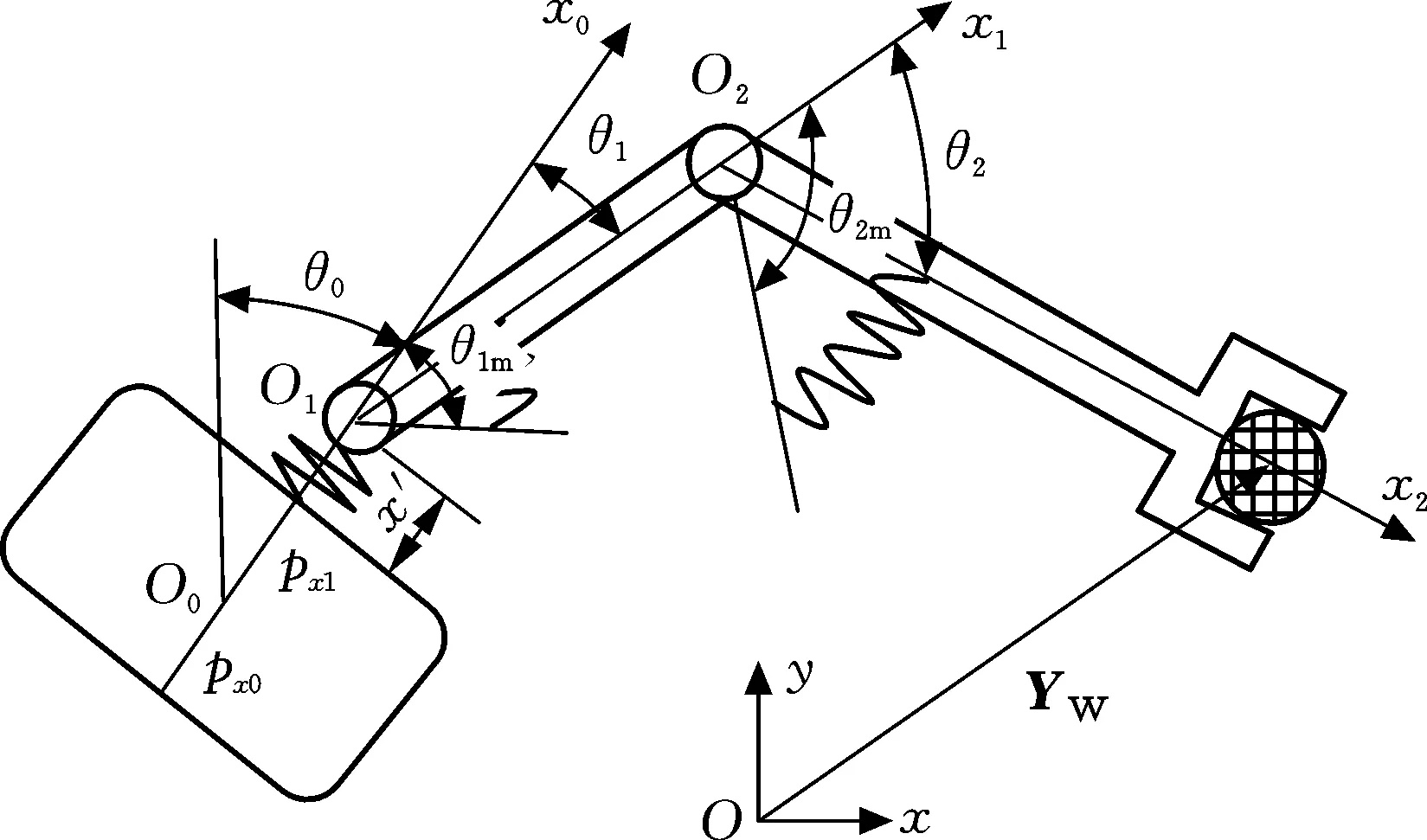
图1 柔性基、柔性关节空间机械臂的系统模型Fig.1 System model of flexible-base and flexible-joint space manipulator
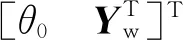
(3)
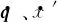
利用式(3)并结合基于等效刚度及奇异摄动技术,设计得到关节电机控制律[14]:
(4)
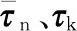
对动力学模型(式(1)、式(2))进行双时标分解,可导出增广惯性空间描述下的慢变子系统:
(5)
Im=diag(0,(kc+I2×2)-1Jm)
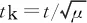
dXk/dtk=AkXk+Bkτk
(6)
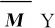
2 自适应鲁棒终端滑模混合自适应最优控制
为实现柔性基、柔性关节空间机械臂基座姿态的调整及末端运动的精确协调运动控制目标,基于奇异摄动模型(式(5)、式(6))设计得到的系统总控制器(慢变子控制器、快变子控制器组合而成)应同时满足如下要求:①慢变子控制器应能克服系统不确定性的影响,使基座姿态及末端运动的实时跟踪误差有效、稳定地收敛至0或一个接近于0的小邻域之内,以保证系统刚性运动具有预期的控制精度;②快变子控制器对基座、关节的振动具有良好的抑制作用。
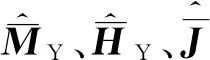
(7)
式中,ρ(t)为新定义的系统广义不确定性函数。
为便于控制器的分析、设计,现对上述系统作如下两个假设[15]:

(8)
假设2不确定函数ρ(t)与系统的控制输入相关,且ρ(t)的范数满足
(9)
式中,bi为系统的不确定上界值,bi>0(i=0,1,2)。
e1=Y-Yd
(10)
(11)
将式(11)代入式(7),得慢变子系统误差方程:
(12)
定义终端滑模函数
(13)
C=diag(c1,c2,c3)
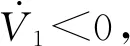
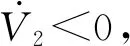
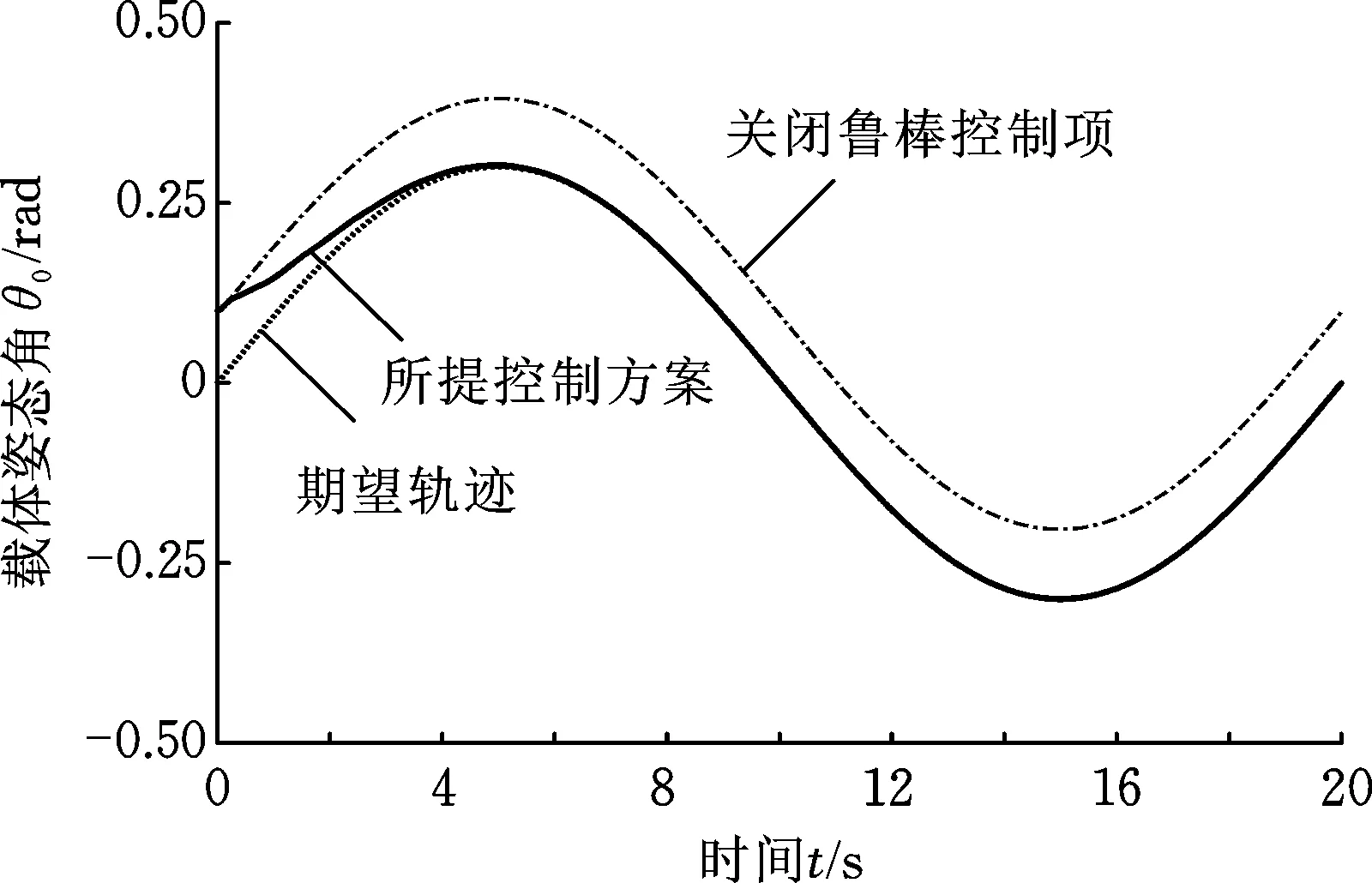
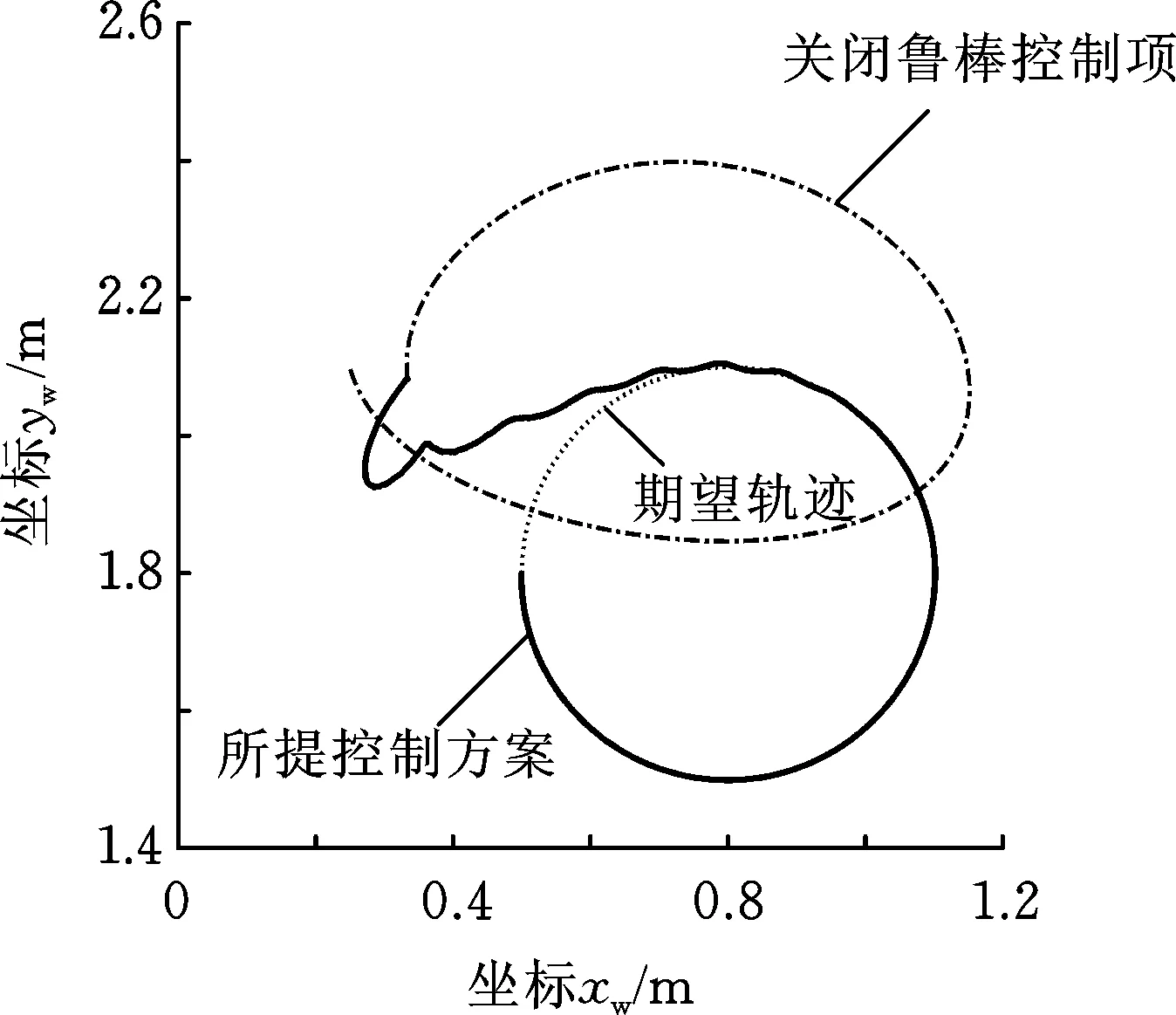
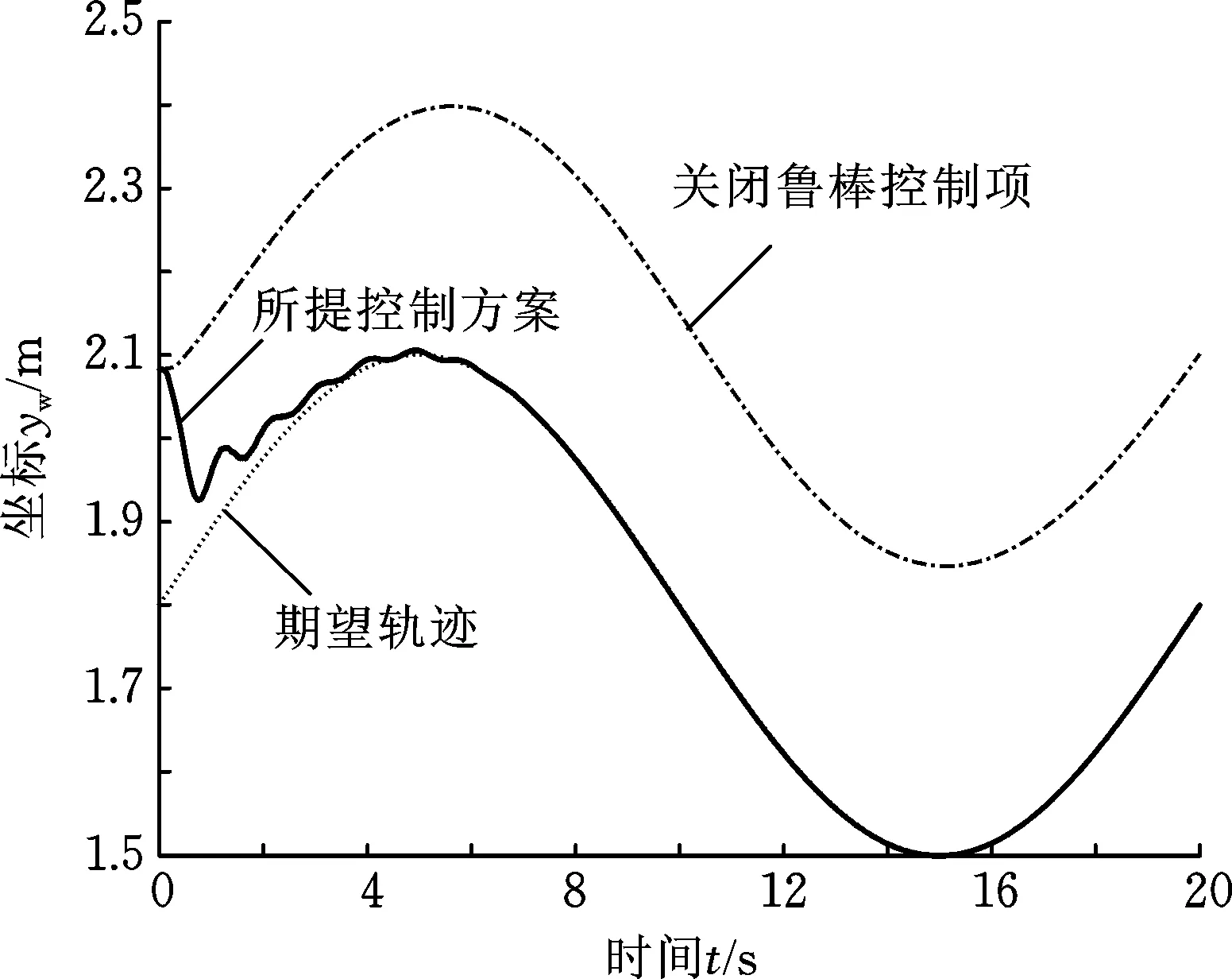
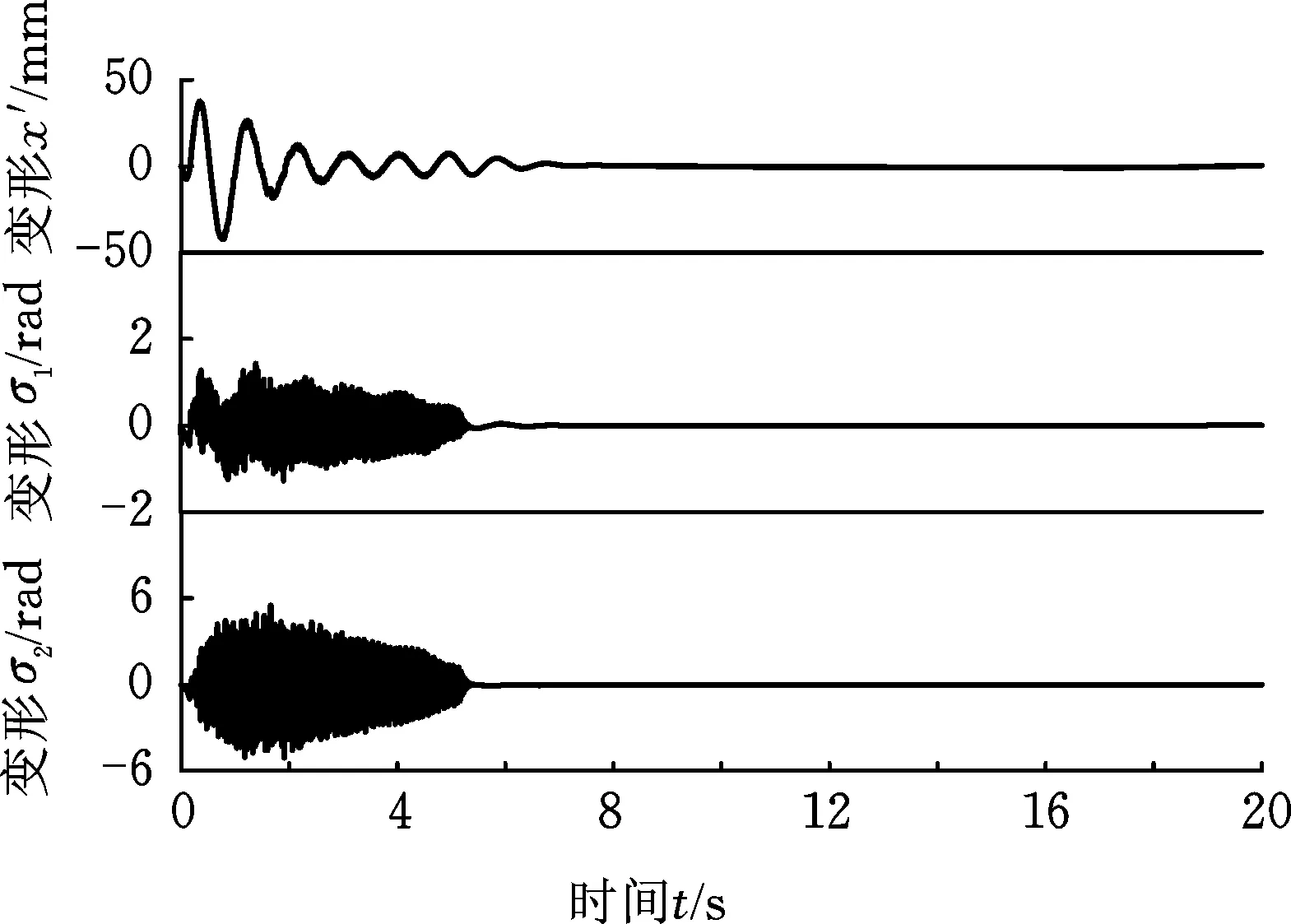
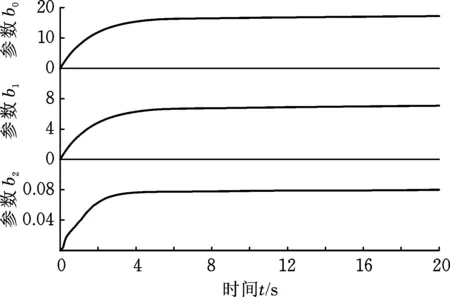
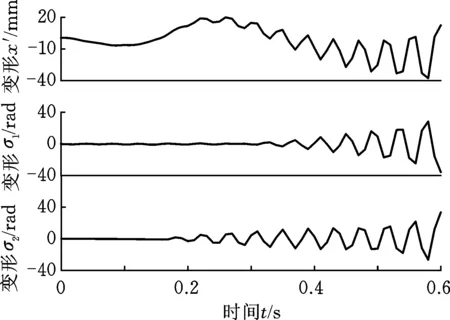
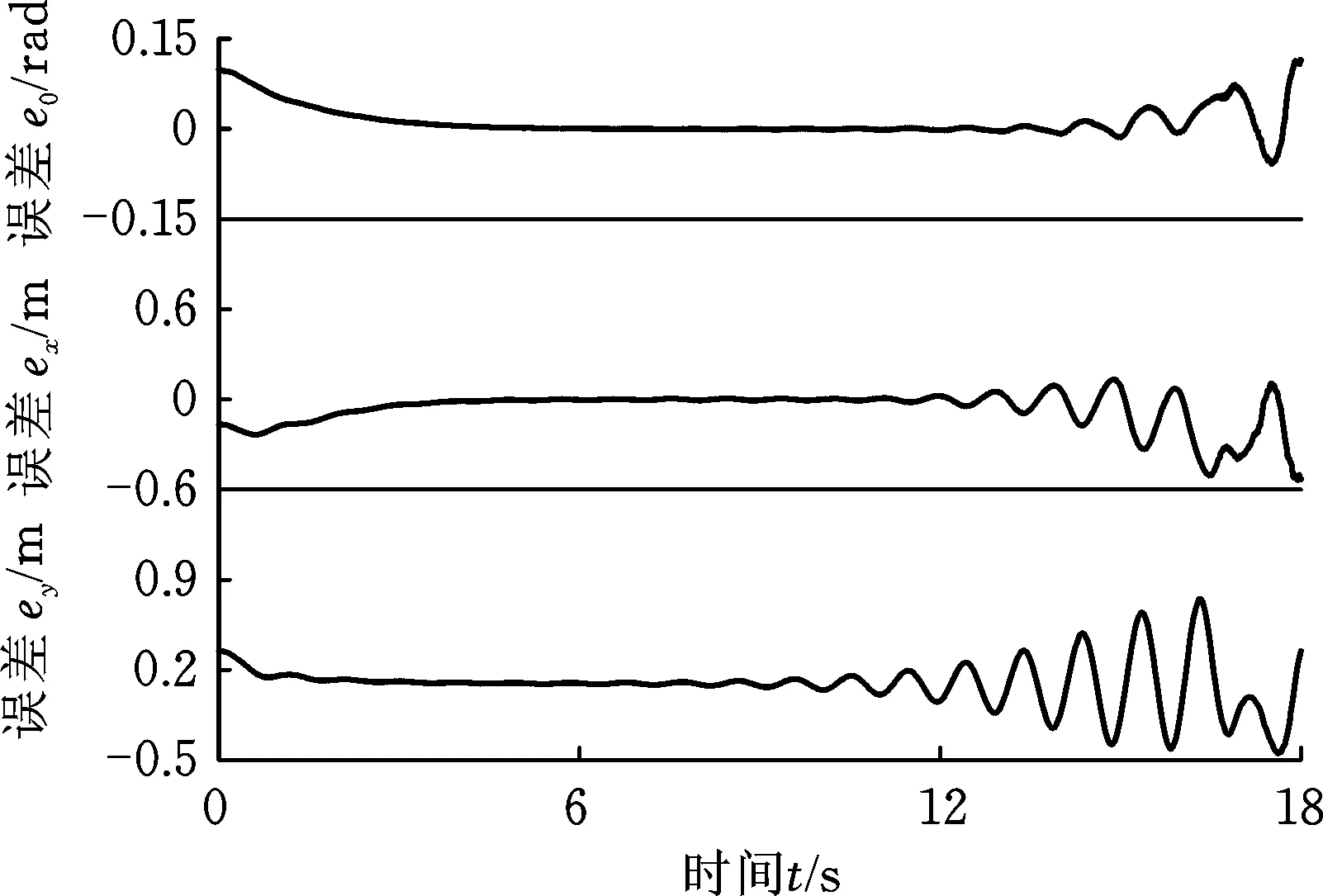
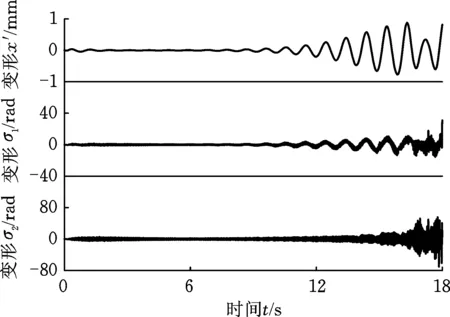
式中,c1、c2、c3为正常数;a、b均为正奇数,a 根据滑模控制理论,为保证控制系统的稳定性,所提控制律需满足滑模到达条件: (14) (15) 若将系统不确定性影响纳入考虑范畴,则需在式(15)的基础上附加设计离散鲁棒控制律: (16) 定理1 对于慢变子系统误差方程(式(12)),由低频等效控制律(式(15))、离散鲁棒控制律(式(16))线性叠加得到的慢变控制律 (17) 可确保慢变子系统跟踪误差渐近稳定地收敛至零。 证明:对李亚普诺夫函数 V1=STS/2 (18) 求导,并考虑式(12)、式(13),有 (19) 将式(15)~式(17)代入式(19),并结合式(9),有 (20) 上述控制律虽能保证系统轨迹的渐近跟踪,但仍存有改进之处:①式(16)给出的鲁棒控制律在系统跟踪误差趋近零点时会出现离散、高频的控制切换,此种不连续的控制极易激发系统基座、关节的柔性振动,反过来影响整个系统的刚性运动控制精度;②式(9)中的bi预估过小,慢变子系统的稳定性难以保证;预估过大,系统控制偏于保守。 为此,下面拟结合边界层法对离散鲁棒控制律(式(16))做如下连续化处理: (21) 式中,δ为小常数,δ>0。 (22) (23) (24) 式中,χi为自适应调节系数,χi>0。 定理2针对慢变子系统误差方程(式(12)),由等效控制律(式(15))、连续鲁棒控制律(式(21))、自适应调节律(式(22)~式(24))组成的慢变控制律(式(17)),可使慢变子系统跟踪误差收敛到零附近的小邻域内且最终一致有界。 证明:对李亚普诺夫函数 (25) 求导并结合式(19),可得 (26) (27) 结合式(22)~式(24)、式(9),式(27)可进一步简化为 (28) 为抑制系统基座、关节在运动过程中产生的柔性振动,采用基于系统能量性能指标函数的自适应最优控制器对快变子系统(式(6))进行主动控制。 (29) (30) 若Z1可测,则可利用自适应观测算法: (31) (32) 对高阶状态Z2进行在线观测[17]。 对式(31)求时间的一阶导数,并利用式(32),整理得 (33) 显然,为使上述观测系统保持稳定,需合理选取Λ以确保式(33)具有负实部的特征值。 (34) 为证实上述理论分析、结果的可行性,拟对图1所示柔性基、柔性关节空间机械臂进行系统仿真控制研究。假设mj、Jj(j=0,1,2,w)表示空间机械臂各分体(下标0对应载体基座,1对应臂杆1,2对应臂杆2,w对应负载)的质量及转动惯量;l0表示x0轴上点px0与px1的距离(载体基座的宽度),l1、l2分别为臂杆1和臂杆2的长度。系统真实参数如下:m0=60 kg,m1=m2=6 kg,mw=3 kg,J0=30 kg·m2,J1=J2=3 kg·m2,Jw=1.5 kg·m2,l0=l1=l2=2 m,J1m=J2m=0.09 kg·m2,k1m=k2m=50 N·m/rad,k0=500 N/m。系统的初始构形为q(0)=[0.1 1.4 3.9]Trad,θm(0)=[1.4 3.9]Trad,x′(0)=0。系统的期望协调运动任务如下: 基座姿态轨迹 θ0d=0.3sin(πt/10) (rad) 负载圆周轨迹 将式(15)、式(21)~式(24)得到的慢变控制律式((17))与基于观测器(式(31)、式(32))得到的快变控制律(式(34))进行线性叠加,可获得系统的混合控制方案。 图2 载体姿态的轨迹跟踪Fig.2 Trajectory tracking ofbase attitude 图3 负载的轨迹跟踪Fig.3 Trajectory tracking of load 图4 xw坐标的轨迹跟踪Fig.4 Trajectory tracking of coordinate xw 图5 yw坐标的轨迹跟踪Fig.5 Trajectory tracking of coordinate yw 图6 系统的柔性振动(所提控制方案)Fig.6 Flexible vibration of the system (the proposed control scheme) 为体现所提方案的控制优势,本文又给出了另外4种不同控制情形下的系统仿真控制结果。 (1)仅关闭方案中的快变最优控制律τk。 图7 参数的调整曲线(所提控制方案)Fig.7 Adjusting curves of parameter (the proposed control scheme) 图8所示为仿真得到的系统基座及两关节在前0.6 s内的柔性振动曲线。显然,若不使用快变控制律τk对系统进行振动的主动控制,基座及关节将在极短的时间内产生大幅度的振动,进而导致系统无法在预期仿真时间内保持稳定并最终发散。 图8 基座及两关节的柔性振动(情形1)Fig.8 Flexible vibration of the base and two joints (case 1) 图9 轨迹跟踪误差(情形2)Fig.9 Trajectory tracking errors (case 2) 图10 系统的柔性振动(情形2)Fig.10 Flexible vibration of the system (case 2) 图11 轨迹跟踪误差(情形3)Fig.11 Trajectory tracking errors (case 3) 图12 不同扰动作用下的跟踪误差(关闭鲁棒控制项Fig.12 Trajectory tracking errors from different disturbances (without the robust control item 图13 轨迹跟踪误差(情形4)Fig.13 Trajectory tracking errors (case 4) 图14 系统的柔性振动(情形4)Fig.14 Flexible vibration of the system (case 4) 本文为解决具有不确定参数和外部扰动的柔性基、柔性关节空间机械臂的控制问题,提出一种由自适应鲁棒终端滑模控制与自适应最优控制相结合的基座姿态、末端负载协调运动混合控制策略。自适应鲁棒终端滑模控制通过对系统不确定函数集中项上界值的自适应估计及控制信号的连续化处理,消除了系统不确定性、控制信号离散对系统刚性运动带来的负面影响,实现了系统期望轨迹的精确跟踪。自适应最优反馈控制可避免对系统高阶快变量进行实时测量,不但保证了快变子系统的稳定性,而且能有效抑制系统基座、关节的柔性振动。理论分析及仿真结果均证实了所提方案的有效性及鲁棒性。
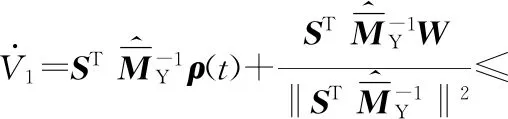
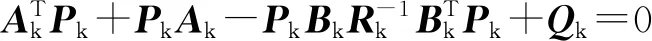
3 仿真结果
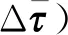

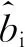
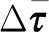
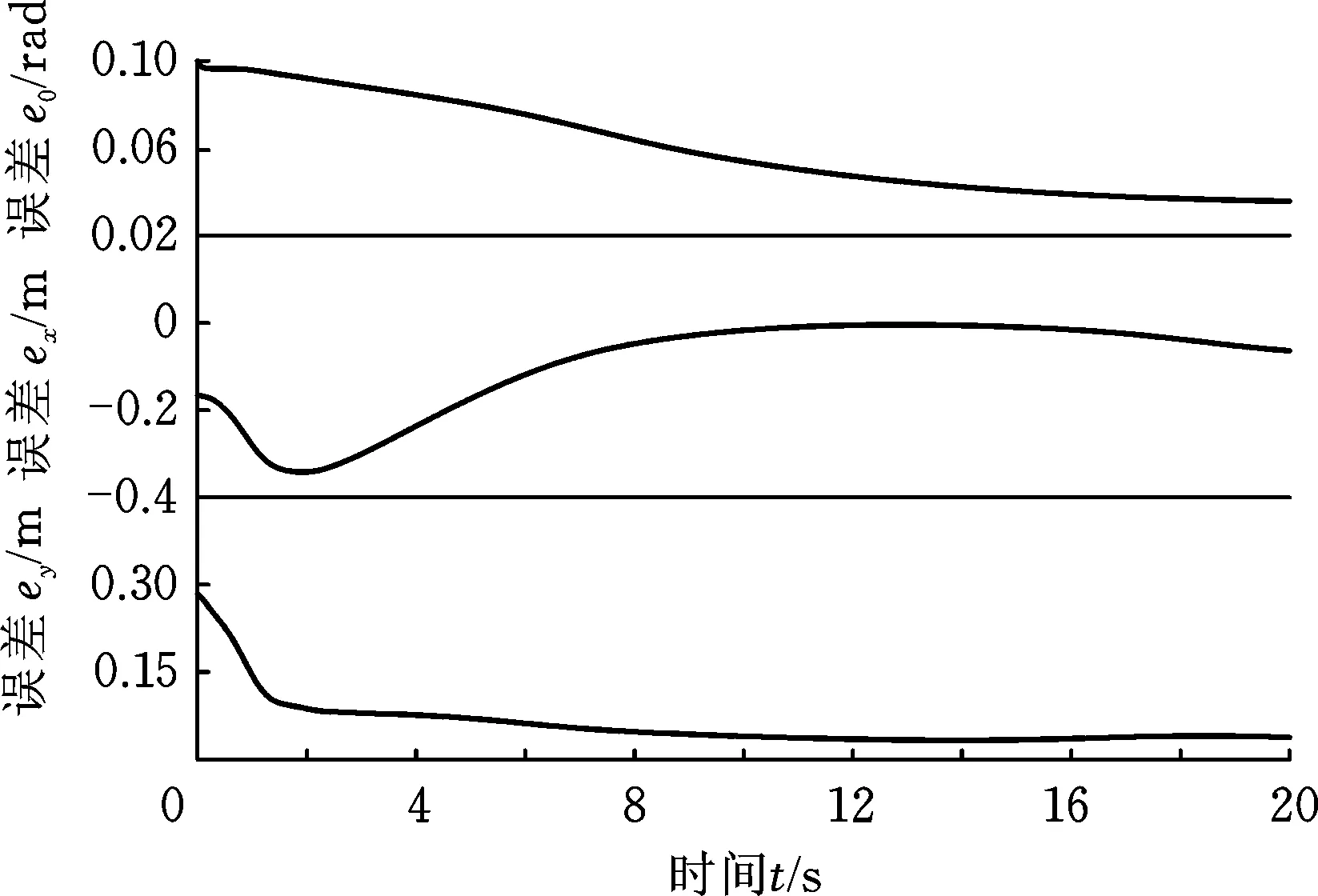

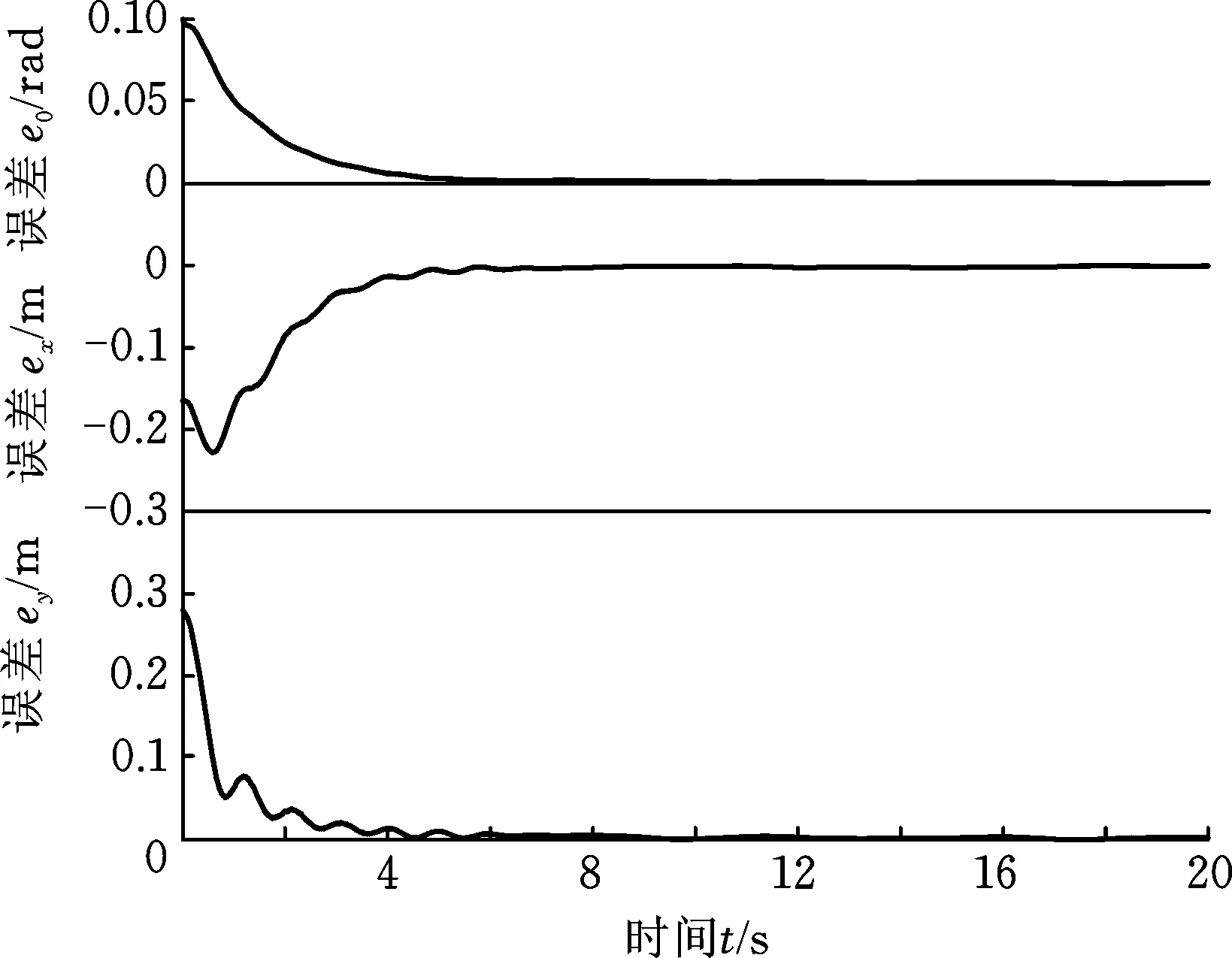
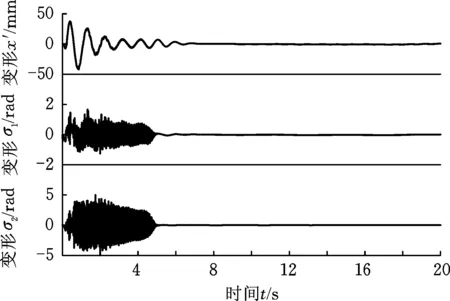
4 结论
