不同贯入度下TBM盘形组合滚刀切削性能分析
2019-07-10刘洪斌刘石头穆伟涛牟浩
刘洪斌 刘石头 穆伟涛 牟浩


摘要:为研究贯入度对TBM盘形组合滚刀顺次回转切削性能的影响,该文以Drucker-Prager塑性准则、岩石力学和滚刀破岩机理为基础,运用ABAQUS建立刀间距为60mm的17in盘形组合滚刀模型,分析不同贯入度下TBM盘形组合滚刀顺次回转破岩的复杂非线性动态响应过程。结果:刀间距一定,组合滚刀顺次回转切削存在一个临界贯入度使破岩区域相交,滚刀间岩石破碎程度最佳,比能耗最小,破岩效率最高;随着贯入度增加,组合滚刀所受三向力大致呈线性递增趋势;组合滚刀切削垂直力与滚动力之比约为4.5,TBM前进推动力约为刀盘旋转扭转力的4.5倍为宜,即需要控制TBM推进速度与刀盘转动速度合适比例关系。
关键词:盘形滚刀;ABAQUS;贯入度;切削性能;三向力
中图分类号:U455.43
文献标志码:A
文章编号:1674–5124(2019)02–0036–06
0 引言
近年来全断面岩石隧道掘进机(tunnel boring machine,TBM)广泛应用于各类隧道及地下工程施工领域,滚刀作为TBM重要组成部分,直接参与岩石破碎过程,其切削性能优劣直接影响到施工效率[1]。单一刀具切削效率低下,不能满足盾构施工快速发展的需要。因此,为提高切削效率,研究盾构组合刀具协同切削性能很有必要。
夏毅敏等[2]采用LS-DYNA模拟盘形滚刀破碎岩石过程,研究滚刀结构参数和工作参数对破岩力的影响特性,并在100t盾构刀具回转切削性能测试实验台上进行实验。M.Entacher等[3]对隧道掘进机刀具测力系统进行设计,监测刀具受力变化;C.Balci等[4]对V型盘形滚刀进行实验和现场调研,研究岩石力学性能对刀具切削的影响。龚秋明等[5]应用机械破岩试验平台研究不同贯入度对破岩效率的影响,研究发现贯入度增加到一定程度后再单纯地增加贯入度不能无限提高破岩效率。谭青等[6]利用离散元法研究在无围压条件下2把TBM刀具同时、顺次切削方式对刀具破岩机理的影響,发现切削顺序决定了岩石的破碎方式,当刀间距大于80mm时,顺次加载方式下的破岩效率不再高于同时加载方式下的破岩效率。程永亮[7]为研究TBM盘形滚刀的破岩效率及其最优贯入度,对双滚刀切削岩石的过程进行三维动态模拟,并利用回转式切削实验台进行双滚刀破岩实验。Mahdi Rasouli Maleki[8]和Isaac Madrid Vergara等[9]都建立了掘进机性能预测模型,并且Mahdi Rasouli Maleki指出隧道掘进机的性能预测是隧道工程补充调查中最重要的措施之一,也是评估某一施工作业所需时间的重要手段之一。综述发现前人并未研究贯入度对组合刀具顺次回转切削性能的影响,因此本文基于前人对滚刀破岩受力及贯入度对滚刀破岩效率的影响等研究,运用ABAQUS建立组合滚刀回转切削岩石模型,研究TBM组合盘形滚刀以顺次回转切削方式在不同贯入度下的切削性能。
1 建立组合滚刀破岩有限元模型
1.1 岩石模型
岩石模型厚度为100mm,宽度为600mm,圆角为13°。TBM工作主要依靠盘形滚刀对岩石进行挤压和剪切来切割岩石,由于岩石复杂力学性质特点,本文建立扩展线性Drucker-Prager模型,模拟岩石塑性本构关系[10-11],如图1所示。
线性D-P本构关系屈服准则:
式中:t——偏应力,MPa;
p——等效压应力,MPa;
β——线性屈服面在p-t应力平面中的斜率,通常指材料摩擦角;
d——材料粘聚力,MPa;
q——Mises等效应力,MPa;
r——偏应力第三不变量;
k——三轴拉伸试验屈服应力与三轴压缩试验屈服应力的比率,即屈服面与中间主应力关系(k=1.0时为曲线m,k=0.8时为曲线n)。
1.2 滚刀破岩动力学模型
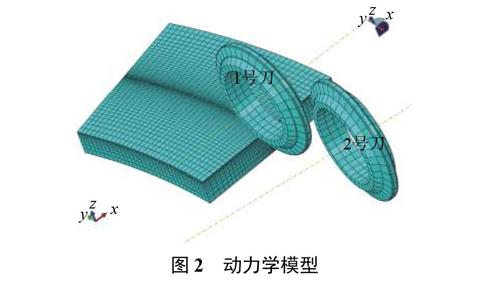
TBM在施工中常遇到各种复杂的地质条件,难以建立全因素模型,须对实际问题进行必要的简化[6]。因此本模型简化为两个17in盘形滚刀刀圈组合顺次回转切削岩石,刀圈间距为60mm,1号刀圈在刀盘上所处位置为半径2.5m处,其动力学模型如图2所示。
刀圈材料为各向同性的线弹性材料,岩石为花岗岩,表1为刀圈—岩石材料参数。岩石失效准则采用ShearDamage和DuctileDamage准则组合。刀圈与岩石采用表面与表面接触,刀刃为主面,岩石上表面为副面。设置罚函数摩擦公式定义切向接触行为,摩擦系数为0.2,法向接触采用ABAQUS默认值。刀圈与岩石形状较规整,故采用三维八节点(C3D8R)线性六面体单元减缩积分划分网格,细划刀圈与岩石接触面处的网格,其余部分粗划,既能提高仿真结果精度,又能节约计算机资源,减少仿真时间[12]。单个刀圈的单元数为1064,岩石的单元数为19200。
1.3 边界条件
对岩石底部施加X、Y、Z三向初始位移及旋转约束,即固定岩石底部,且不考虑岩石围压。在1、2号刀圈质心分别建立参考点RP-1和RP-2,并设置各自参考点与刀圈采用绑定约束,以定义刀圈自转角速度;在刀盘中心建立参考点RP-3,和刀盘中心Z方向上一定位置建立参考点RP-4,将1号刀圈与参考点RP-3设置为刚体约束,将2号刀圈与参考点RP-4也设置为刚体约束,以定义刀圈公转角速度。
ω0=V/R (3)
ω=V/r (4)
式中:R——刀圈安装半径,mm;
ω0——刀盘转速,r/min,即刀圈公转角速度,rad/s;
ω——刀圈自转角速度,rad/s;
v——刀圈平动速度,即线速度,mm/s;
r——刀圈半径,mm。
定义刀圈Z向速度为–5mm/s,即给定TBM推进速度;设刀盘转速ω0=1r/min=0.1047rad/s,即RP-3和RP-4绕Z轴旋转角速度为0.1047rad/s,由式(3),则刀圈平动速度为v=261.75mm/s,假设刀圈与岩石之间无相对滑动,由式(4),RP-1和RP-2绕X轴旋转角速度为ω=1.212rad/s。
2 仿真结果分析
2.1 岩石失效等效塑性应变云图
模拟盘形组合滚刀在2,4,6,8,10,12mm6种不同贯入度下顺次回转切削岩石过程,得到岩石应变云图如图3所示。分析云图可以发现:两把盘形组合滚刀刀间距一定,在贯入度较小时,如图3(a)、图3(b)所示,贯入度2mm和贯入度4mm,岩石发生很小程度的等效塑性变形,即滚刀滚压后中间形成微小破碎区,很少岩屑从母岩上剥落,并留有很大岩脊;随着贯入度增加,如图3(c),贯入度达6mm时,岩石发生较明显等效塑性变形,即两把滚刀间形成相应破碎区,但破碎区未贯通,可是滚刀间岩脊变小;如图3(d),贯入度达8mm时,岩石发生很明显等效塑性变形,滚刀间形成一定破碎区,破碎区基本贯通,即两把滚刀间的岩石已大部分破碎,但仍存在很小岩脊;如图3(e),贯入度增加到10mm时,滚刀间形成贯通破碎区,即滚刀间的岩石刚好完全破碎;如图3(f),贯入度增加到12mm时,由于滚刀间产生的侧向裂纹未能交汇,以致滚刀间的破碎区未能完全贯通,即两把滚刀间的岩石过渡破碎,且岩石破碎块度较大,与贯入度10mm时相比,滚刀组合顺次回转切削破岩效果不佳,切削效率趋于下降趋势,此时滚刀破岩贯入度超过临界值。
2.2 岩石临界贯入度处裂纹分析
由岩石应变云图,贯入度从4mm增加到6mm,岩石变形破碎趋明显。根据贯入度物理定义,随着贯入度增加,滚刀刀圈与岩石接触面积增大,接触应力也随之增大,再由滚刀破岩机理(滚刀绕刀盘中心公转和随自身质心自转,滚刀将会在刀盘转动和推动下产生扭转力和推动力[13]),岩石受到滚刀挤压和剪切作用力变大,因此会加大裂纹产生和扩展延伸。基于谭青等[14]对不同刀间距情况下相邻滚刀协同切削模式和非協同切削模式下破岩区域分析,刀间距为60mm,贯入度增加达到临界值10mm时,两滚刀间水平裂纹和侧向裂纹交汇,滚刀间岩石刚好完全破碎,如图4所示。水平裂纹交汇上方将会形成剪切破碎区,此区域岩石被剪切破坏,水平交汇裂纹下方和侧向裂纹交汇内部将会形成挤压破碎区,此区域岩石被挤压破坏。贯入度小于此临界值时,滚刀间裂纹不能交汇,中间留有岩脊;贯入度过大,能耗较大,滚刀刀刃深入岩石过深,刀刃易损伤,且中间侧向裂纹不能交汇,为过渡破碎状态。
2.3 滚刀下方岩石节点应力分析
选取岩石底部第557号节点,如图5所示,提取6种不同贯入度下1号滚刀破岩时该节点应力值,绘制曲线如图6所示。可以看出:因1号滚刀切削对周围岩石产生了一定损伤,随着贯入度增加,该节点应力总体呈上升趋势,且不会马上消失。仿真后处理发现,组合滚刀顺次回转切削,开始1号滚刀先行切削岩石,每一时刻滚刀最大接触应力都在1号刀上,当2号刀进行切削,每一时刻滚刀最大接触应力都转换到2号刀上,因为1号滚刀切削时留下的残余应力没有马上消失,2号滚刀切削时发生应力叠加。因此,当2号滚刀滚压时岩石存在较大残余应力,这部分残余应力会对2号滚刀切削提供良好的破岩条件。
2.4 组合滚刀所受三向力分析
通过ABAQUS有限元仿真分析和数值计算,
得到不同贯入度下组合滚刀顺次回转切削所受三向力平均值,绘制曲线如图7所示。从图中可以看出:1)在贯入度相同的情况下,1号滚刀(靠近刀盘中心,且先行切削破岩的滚刀)所受三向力都比2号滚刀(远离刀盘中心,且随后切削岩石的滚刀)所受三向力大,因为1号刀先行挤压剪切破岩,待2号刀切削时,滚刀左侧岩石围压变小,对刀具挤压力减小;2)随着贯入度增加,1号和2号滚刀所受三向力大致呈线性递增趋势,因为贯入度越大,滚刀与岩石接触面积越大,同样转速和推力下,滚刀受力越大;3)在贯入度相同的情况下,1号滚刀滚动力约为2号滚刀滚动力的1.5倍,1号滚刀垂直力约为2号滚刀垂直力的2倍,说明靠近刀盘内侧先行破岩的刀具对切削过程起着重要作用;4)在贯入度相同的情况下,滚刀所受三向力中,垂直力最大,滚动力次之,侧向力最小,说明滚刀破岩过程中主要是靠刀圈挤压和剪切联合破岩,即TBM前进推动力和刀盘旋转扭转力协同作用的结果;5)由图7(c)可以看到,滚刀所受垂直力Fv与贯入度h基本上成正比例关系,过大的贯入度会产生较大的垂直力,从而导致刀圈断裂,因此,贯入度不是越大越好;6)由图7(d)可知,组合滚刀顺次回转切削垂直力与滚动力之比约为4.5,说明TBM前进推动力约为刀盘旋转扭转力的4.5倍为宜。
2.5 比能与贯入度关系
对仿真结果进行处理,得到贯入度与比能的关系,如图8所示。从图中可以看出,随着贯入度增加,整体上组合滚刀顺次破岩比能呈递减趋势,在临界贯入度10mm时比能达到最低值,超过临界贯入度,比能随贯入度的增加而增加。说明贯入度增加使扭矩和破碎岩石的体积均增加,同时二者比值减小,从而减小比能,提高了TBM的破岩效率。HongsuMa等[15]分析了贯入度与比能的关系,随着贯入度不断增加,比能达到了过渡点的最低值,超过这一点,比能随贯入度的增加而增加,与图8曲线走势较符合,也间接说明本模型的合理性。
3 结束语
通过运用ABAQUS建立刀间距为60mm的17in盘形组合滚刀模型,分析贯入度分别为2,4,6,8,10,12mm时滚刀顺次回转切削性能,得到如下结论:1)刀间距一定的条件下,组合滚刀顺次回转切削存在一个临界贯入度使破岩区域相交,滚刀间岩石破碎程度最佳,比能耗最小,破岩效率最高。因此,在临界贯入度下TBM工作,会加快施工进度。2)随着贯入度增加,组合滚刀所受三向力大致呈线性递增趋势,说明TBM工作时贯入度不能太大。1号滚刀比2号滚刀所受同种三向力都大,因为1号刀先行挤压剪切破岩,待2号刀切削时,滚刀左侧岩石围压变小,对刀具挤压力减小,从而对刀具损伤减小,提高刀具耐用度,减少换刀。3)组合滚刀顺次回转切削垂直力与滚动力之比约为4.5,说明TBM前进推动力约为刀盘旋转扭转力的4.5倍为宜,即需要控制TBM推进速度与刀盘转动速度合适比例关系。
参考文献
[1]刘洪斌,穆伟涛,李萍瑛,等.刀圈线型对盾构滚刀破岩效率影响分析[J].煤矿机械,2015,36(10):125-126.
[2]夏毅敏,欧阳涛,陈雷,等.盘形滚刀破岩力影响因素研究[J].应用基础与工程科学学报,2012,20(3):500-506.
[3] ENTACHER M, WINTER G, BUMBERGER T, et al. Cutter force measurement on tunnel boring machines-System design[J]. Tunnelling and Underground Space Technology,2012, 31(11): 97-106.
[4] BALCI C, TUMAC D. Investigation into the effects of different rocks on rock cuttability by a V-type disc cutter[J]. Tunnelling and Underground Space Technology, 2012, 30(18): 183-193.
[5]龚秋明,何冠文,赵晓豹,等.不同贯入度对掘进机滚刀破岩效率的影响[J].现代隧道技术,2016,53(1):62-68.
[6]谭青,徐孜军,夏毅敏,等.2种切削顺序下TBM刀具破岩机理的数值研究[J].中南大学学报(自然科学版),2012,43(3):940-946.
[7]程永亮.TBM盘形滚刀破岩最优贯入度的数值模拟[J].中南大学学报(自然科学版),2017,48(4):936-943.
[8]MALEKIMR.RockJointRate (RJR); anewmethodforperformancepredictionoftunnelboringmachines (TBMs) inhardrocks[J].TunnellingandUndergroundSpaceTechnology, 2018, 73(22): 261-286.
[9]VERGARAIM, SAROGLOUC.PredictionofTBMperformanceinmixed-facegroundconditions[J].TunnellingandUndergroundSpaceTechnology, 2017, 69: 116-124.
[10]李辉,王树林,汪加科.TBM盘形滚刀受力分析[J].现代隧道技术,2012,49(3):193-197.
[11]王騰跃.TBM盘型滚刀关键技术及试验装置研制[D].沈阳:沈阳建筑大学,2011.
[12]张珂,王腾跃,孙红,等.全断面岩石掘进机盘形滚刀破岩模拟[J].沈阳建筑大学学报(自然科学版),2010,26(6):1209-1213.
[13]袁超,唐莉梅,余立新,等.盾构机盘形滚刀刀圈与地层适应性分析[J].隧道建设,2009,29(增刊1):9-11.
[14]谭青,易念恩,夏毅敏,等.全断面岩石掘进机滚刀最优刀间距计算公式研究[J].岩土力学,2016,37(3):883-892.
[15]MAHS, GONGQM, WANGJ, etal.StudyontheinfluenceofconfiningstressonTBMperformanceingraniterockbylinearcuttingtest[J].TunnellingandUndergroundSpaceTechnology, 2016, 57(20): 145-150.
