考虑可信度的犹豫模糊多属性决策方法研究

崔春生， 朱向琳， 任亚丹， 祝晓梦

(1.河南财经政法大学 计算机与信息工程学院，河南 郑州 460046； 2.西北工业大学 管理学院，陕西 西安 710129； 3.郑州工商学院 工学院，河南 郑州 451400)

0 引言

作为一项贯穿于日常生活的基本活动，决策在国家建设、政治、军事、贸易和农业等领域也发挥着不容忽视的作用和影响。在现实决策问题中，由于考虑因素较多，决策者容易出现犹豫不决、难以抉择的情形，因此无法直接用经典模糊理论描述和建立决策模型。针对决策过程中存在的问题，2010年，Torra和Narukawa提出犹豫模糊集的相关概念和思想，它容许一个元素的隶属度可以存在不止一个值[1,2]。在他们的文章中，一些犹豫模糊集的基本运算被提出，并将它与另外的几种拓展模糊集的区别与联系也进行了深入对比和讨论。犹豫模糊集的一个主要优点就是容许存在多个不同的隶属度，因此评价过程中各属性值可以用一个犹豫模糊数来表示，各决策方案则组成一个犹豫模糊集。为了能够处理不同犹豫模糊环境下的信息，人们提出了各种集成算子的实际需要。有序加权算术平均(OWA)算子是有关信息集成方式的最基础的研究，后来Chiclana F等学者在此基础上进行了拓展，提出了有序加权几何平均(OWG)算子，并基于此提出了一种应用于乘法偏好关系的决策方法[3]。OWG是一种基于几何平均的信息集成算子，后来学者Yager将其扩展为一种广义有序加权平均算子及诱导的有序加权平均算子[4]。在此研究基础上，Fodor J等学者在文献中基于指数和拟算术平均的概念，给出了广义对数有序加权平均(GOWA)算子和拟平均有序加权算术平均(QOWA)算子的概念和形式[5]。Merigo J M 等学者在文献中基于GOWA算子、IOWA算子以及QOWA算子的概念和特点，将三种集成算子结合起来，得到一种新的算子，即广义诱导有序加权平均(IGOWA)算子[6]。Yager详细介绍了连续有序加权算数平均(COWA)算子和连续有序加权几何平均(COWG)算子的定义和算法，通过决策问题的实际应用验证了其可行性和有效性[7]。

虽然集成算子的研究和应用一直受到学者们的广泛关注，但在复杂的现实决策问题中，往往存在决策专家犹豫不决的情形，且基于集成算子的决策问题具有一定的复杂性及深度，因此需要对其进行深入研究，探讨新的信息集成方法。

1 预备理论

1.1 犹豫模糊集的基本概念

在现实多属性决策问题中，往往存在不确定性信息。比如求职者在选择工作单位过程中，必须综合考虑每个工作单位的工资水平、晋升空间和企业文化等因素；又如供应商的选择问题。为生产单位选择合适的供应商时，不仅仅局限于对产品价格的评估，还应当同时考虑产品质量和供货能力等因素。但由于专家的背景知识领域或专业水平有所差异，导致一个属性存在多个评价值的情形，基于此Torra[1]给出的犹豫模糊集恰好准确的描述了这一问题。

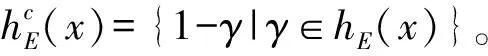
另外假设犹豫模糊数所含个数有限，可用hσ(j)(x)表示hE(x)所有元素中第j小的元素。

例1设X={x1,x2,x3}为一个给定的集合，其中hE(x1)={0.2,0.4,0.5}，hE(x2)={0.3,0.4},hE(x3)={0.3,0.2,0.5,0.6}分别表示xi(i=1,2,3)关于E的隶属度所组成的集合。那么，E就被称为一个犹豫模糊集，可以表示为：

E={,

x2<0.3,0.4>,x3<0.3,0.2,0.5,0.6>}

定义2[1,8]设E={{x,hE(x)}|x∈X}是一个犹豫模糊集，可以给出以下定义：

(1)如果对任意的x∈X，有hE(x)=0，则称E为空犹豫模糊集；

(2)如果对任意的x∈X，有hE(x)=1，则称E为绝对犹豫模糊集；

(3)如果对任意的x∈X，有hE(x)=[0,1]，则称E为完全犹豫模糊集。

对于犹豫模糊数h1和h2，下面给出二者之间大小的对比法则：

(1)如果s(h1)>s(h2)，则h1≻h2；

(2)如果s(h1)=s(h2)，则h1=h2。

定义4[8,10]设λ>0，h，h1和h2是三个犹豫模糊数，它们的一些基本运算定义如下：

(1)h1∪h2=H{max(γ1,γ2)|γ1∈h1,γ2∈h2}；

(2)h1∩h2=H{min(γ1,γ2)|γ1∈h1,γ2∈h2}。

举例来说明，设h1和h2是两个犹豫模糊数，其中h1={0.2,0.3,0.6,0.8}，h2={0.4,0.5,0.6,0.9}，那么h1与h2的并和交分别为：

h1∪h2={0.4,0.5,0.6,0.8,0.9}
h1∩h2={0.2,0.3,0.4,0.5,0.6,0.8}

定义5[8,9]设α>0，h，h1和h2是三个犹豫模糊数，则：

1.2 犹豫模糊加权平均(HFWA)和几何(HFWG)算子

加权平均(WA)算子与加权几何(WG)算子是在经典决策科学理论中使用最多的集成算子。在多属性决策过程中，它们被国内外学者进行了深入研究，已被推广到不同类型决策信息的集成。

基于犹豫模糊集的特点，Xia与Xu[11]分别将加权平均(WA)算子与加权几何(WG)算子与犹豫模糊数相融合，得到了两种犹豫模糊集成算子：

(1)犹豫模糊加权几何(HFWG)算子

定义6设hj(j=1,2,…,n)是一组犹豫模糊数，则有

HFWG(h1,h2,…,hn)

(1)

(2)犹豫模糊加权平均(HFWA)算子

定义7设hj(j=1,2,…,n)是一组犹豫模糊数，则有

HFWA(h1,h2,…,hn)

(2)

1.3 犹豫模糊有序加权平均(HFOWA)和几何(HFOWG)算子

有序加权平均(OWA)算子和有序加权几何(OWG)[3]算子首先将集合内的元素进行排序，然后进行加权集成，值得注意的是，权重wj只与相应的位置j有关。

(1)犹豫模糊有序加权平均(HFOWA)算子

定义8设h1,h2,…,hn为一组犹豫模糊集，设HFOWA：Ωn→Ω，则

HFOWA(h1,h2,…,hn)

(3)

(2)犹豫模糊有序加权几何(HFOWG)算子

定义9设h1,h2,…,hn为一组犹豫模糊集，设HFOWG：Ωn→Ω，则

(4)

这样看来，有序加权算子中的权重向量其实就是位置权重，并且其权重向量的确定方法类似于属性权重。这种方法有很多，比如说一种基于正态分布的方法，该方法根据正态分布的特点，主张为两端的数据应赋较小的权重。但是此类算子仅仅与位置相关联，与专家给出的决策数据大小无关。再比如说直接将两端评价值舍去的决策方法，把最高与最低分去掉之后再进行计算。这种方法虽然便于理解、计算方便，但是存在一定的缺陷。并且，大多数方法没有考虑专家对被评判领域的熟悉程度(即可信度)对决策结果的影响，可能导致决策结果存在偏差。

2 可信度条件下的犹豫模糊多属性决策模型

随着社会分工逐渐细化，为保证多属性决策过程中专家评价数据的合理性和准确度，需要考虑决策专家对被决策领域的知识水平和熟知程度。基于此目的，本文引入可信度的概念，表示决策专家对待决策领域的熟悉程度。

步骤1由决策专家同时给出各备选方案ui∈U下的所有属性cj∈C的犹豫模糊决策值及相应可信度，一起构成犹豫模糊决策矩阵Di=(hijk)m×m×p。

步骤2本文通过RCIHFOWG算子对决策问题中各备选方案的每个属性信息进行集成，并获得Gj的综合决策值为：

Gj=RCIHFOWG(h1,h2,…,hn)

(5)

步骤3本文通过犹豫模糊加权几何(HFWG)算子集结决策专家组成员提供的各备选方案属性信息，求出各备选方案的相应群体综合表现值；

步骤4通过比较上一步骤中计算出的结果，得到该决策问题中每个备选方案ui(i=1,2,…,m)的优劣次序，进一步从备选方案中选出最满意方案。

3 案例应用

M公司作为一家知名的汽车厂家，近几年来业务不断发展壮大，已经陆续在中国多个地市建立基地。截止2017年12月底，M公司全年的累计产销已达206万辆。然而，汽车行业正面临着越来越严峻的挑战，中国汽车市场逐渐进入“微增长”的新常态。为保证公司能够继续稳健发展，如何打破固有的思维套路，提升供应商管理质量，提高客户的综合满意度，是M公司必须尽快找到解决办法的重要发展课题。现M公司需要采购一种汽车离合器，通过市场调查和研究，从众多供应商中选择四家作为备选方案，分别为供应商A1、供应商A2、供应商A3和供应商A4。

现将四个汽车离合器供应商记为U={u1,u2,u3,u4}，(i=1,2,3,4,其中，m=4)，属性集一共包含3个属性，分别为供货能力、价格和产品质量，我们记做C={c1,c2,c3}(j=1,2,3, 其中,n=3)。属性集中各个属性的权重向量分别为w={w1,w2,w3}={0.25,0.3,0.4}。

邀请每位专家对各个供应商的每一属性进行匿名评估，对于每一方案，专家对各个属性给出的评估值构成的犹豫模糊数，为便于下文分析，我们将其记做aij。在决策者对所有方案按各属性评估测度时，由于决策小组中的成员专业知识水平和实践经验有所差距，因此需同时给出相应可信度，如表3～1所示。如a11={(0.8,0.5),(0.6,0.7),(0.6,0.8)}表示对于产品质量属性，专家小组一共给出3种不同的观点，也就是说供应商A1满足属性产品质量的程度分别有0.5，0.7，0.8三种。隶属度的可信度用a11中的二元组第一个分量表示，意味着决策者给出的对该领域的熟悉程度(专业程度)，分别是0.8，0.6，0.6。

步骤1我们采用犹豫模糊决策矩阵的方式表达专家提供的所有评估数据，给出具有可信度的犹豫模糊决策矩阵如表1所示。

表1 犹豫模糊决策矩阵

步骤2利用RCIHFOWG算子得到各个供应商的各属性信息的个体综合表现值，具体情况如表2。

步骤3根据给出的属性权重信息利用犹豫模糊加权几何(HFWG)算子对供应商ui的每个属性信息cj(j=1,2,…,n)进行计算，求得供应商Ui的群体综合表现值：

HFWG(u1)=0.656,HFWG(u2)=0.654,

HFWG(u3)=0.712,HFWG(u4)=0.708

表2 各个供应商的各个属性信息的个体综合表现值

步骤4通过运用犹豫模糊数的比较规则，将各方案ui(i=1,2,…,m)按照大小关系进行排序:HFWG(u3)>HFWG(u4)>HFWG(u1)>HFWG(u2),即方案排序为u3≻u4≻u1≻u2。

从结果可以看出，M公司应选择方案，即M公司应该选择供应商A3作为最佳合作伙伴。

4 结论

在现实世界中，随机性与模糊性信息往往与客观现象如影随形，导致人们对事物的认识总是不完整、不精确的。如何有效处理包含犹豫模糊信息的多属性决策问题已成为国内外学者们的研究热点。本文主要针对犹豫模糊多属性决策问题进行理论及其应用研究，在现有理论研究的基础上，引入专家可信度的思想，构建一种考虑可信度的犹豫模糊集成算子。该算子考虑到专家对决策问题的熟悉程度或专业水平，能够帮助决策者做出更加科学的选择。最后，本文将该决策方法应用在供应商选择的实际问题，验证该方法的有效性。该研究不仅充实了犹豫模糊信息集成理论，而且可以为实际多属性决策问题提供理论依据和方法指导。