抗灾型配电网网架规划方法研究
2019-07-10施鹏佳张林垚张良一王孝慈董树锋
施鹏佳,雷 勇,张林垚,张良一,王孝慈,董树锋
(1.国网福建省电力经济有限公司经济技术研究院,福州 350000;2.浙江大学 电气工程学院,杭州 310027)
0 引言
配电网处于电力系统末端,直接向用户供电,如何使配电网更安全、经济,是配电网规划和运行过程中的重要任务,同时,配电网规划也是整个电力系统规划的重要组成部分[1]。配电网规划包括变电站选址、网架规划、馈线路径选择、馈线型号选择及用户实际需求匹配等多方面因素,是一个综合性问题,其数学本质是一个复杂的离散性、非线性、多目标的组合优化问题[2]。统筹考虑可靠性与经济性的多目标分层规划模型,本文主要讨论配电网网架规划问题。
对于网架规划问题,现在已有较多的研究,文献[3]以网架的停电成本为目标函数,运用改进遗传算法进行求解。文献[4]综合考虑配电网的经济性与可靠性,最终以投资费用、运行费用和网损费用最小为目标对配电网的网架进行多目标规划。文献[5]考虑电网的建设成本和网损,采用蚂蚁算法对配电网进行规划。文献[6]建立了统筹考虑可靠性与经济性的多目标分层规划模型。上述文献以不同成本作为目标函数,采用不同的智能优化算法进行求解,取得了不错的成果,但在配电网网架规划中很少考虑网架的建设成本与受灾风险的影响。
对一些自然灾害频发的地区,在进行配电网规划时应考虑到自然灾害可能产生的影响,使自然灾害对配电网的影响降到最低。本文主要研究考虑灾害风险的配电网网架规划问题,根据待规划地区历史受灾情况绘制受灾地图,求得在不同地区进行网架建设的受灾风险,再结合网架的建设成本与受灾风险,在规划中引入中间节点,并在可行区域内寻优,建立抗灾网架规划的Steiner(斯坦纳)树数学模型,使用模拟退火算法进行求解。实例证明,本文方法得到的配电网网架结构能够有效降低网架建设的总费用,使配电网网架规划更经济。
1 防灾型网架规划问题
配电网网架规划的目标是在满足灾害条件下重要用户供电需求的前提下,使网架建设成本和受灾风险最小,是一个离散性、非线性的组合优化问题。对于防灾型网架规划问题,其网架建设成本主要取决于网架线路的长度,而要使线路长度最小,目前的方法是求解连接电源和负荷节点的最小生成树,这种方法虽易于实现,但无法保证求出的线路总长度最小。本文考虑通过增加中间节点的方法来减少网架线路的总长度,即求解线路长度的Steiner 最小树。
Steiner 最小树问题[7-10]是通过一系列Steiner点找到一棵连接所有需求节点成本最小的树,是一个经典的组合优化问题。Steiner树问题的求解时间会随着Steiner点的规模成倍增加,一般采用智能优化算法求解[11-13]。
以图1 为例说明如何通过增加中间节点来减少网架线路的总长度,增加中间节点后,线路长度从5.4 减少到3,可以看出,相比于最小生成树,增加中间节点的方法可以显著减少网架线路的总长度。
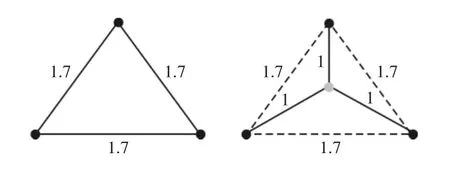
图1 通过增加中间节点来减少网络的总长度
对于防灾型网架规划,若采用增加中间节点的方法,网架的建设成本则包括线路的建设成本和所增加节点的成本两部分。其中所增加节点的成本又包括两部分,即节点处杆塔的建设成本和杆塔建设处的受灾风险。
于是,防灾型网架规划就可以看作一个求解欧氏Steiner 最小树的问题[14],由此可以得到防灾型网架规划的数学模型,其目标函数为:
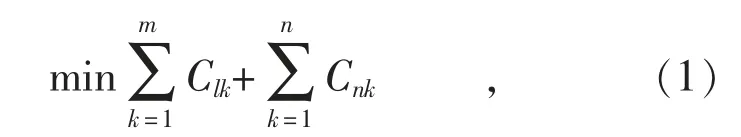
式中:Clk为第k 条线路的建设成本;Cnk为计及灾害风险的第l 根增加节点处杆塔的建设成本;m为线路数量;n 为待建杆塔数量。Cnk与节点所处位置的受灾风险有关,对受灾风险大的地区,为达到抗灾的目标,在建设时需对线路和杆塔进行差异化设计,使得建设成本提高。 受灾风险越大,则Cnk越高。
同时,还应考虑规划时的相关约束,如电网潮流约束、节点电压约束等。
潮流约束:
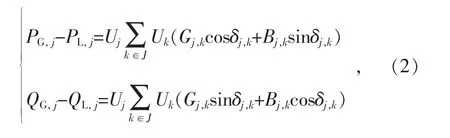
式中:PG,j,QG,j分别为节点j 处注入的有功功率和无功功率;PL,j,QL,j分别为节点j 处负荷的有功功率和无功功率;Gj,k,Bj,k分别为线路的电导和电纳;Uj为节点j 处的电压;Uk为节点k 处的电压;δj,k为节点j 与节点k 电压的相角差;J 为所有节点的集合。
节点电压约束:

式中:Uj为节点j 的电压;Umax,j和Umin,j分别为节点j 的最大允许电压和最小允许电压。
增加节点处杆塔的建设成本与节点所在位置的受灾风险密切相关。一个地区的受灾风险由多种因素决定,如地理位置、地形、灾害等级等,对配电网网架规划区域来说,不同地区的地形、气候条件差异可能很大,对不同地区的受灾风险有直观的认识将有助于指导规划,因此可绘制灾害地图,把不同地区的抗灾建设成本标注在图中,用以指导配电网规划。
2 灾害地图的绘制
灾害地图的主要功能是:输入地图上的坐标,即可输出该地的电网抗灾建设成本。电网规划人员在进行抗灾型电网网架规划时,可查阅灾害地图,考虑不同电网网架的防灾建设成本,从而实现兼顾经济性与抗灾性的电网网架建设。
绘制灾害地图的关键技术是通过蚁群聚类算法,将各个地区根据电网受气象灾害特征划分等级。该等级可以反映在该地区新建电网,其受气象灾害影响的严重程度。每个地区的灾害等级直接影响在该处修建电网的成本,灾害等级越高,修建电网的抗灾建设成本就越高。
2.1 电网自然灾害信息提取
电网建设位置的自然条件对电网抗灾性有很大影响,为了表征这种影响,为每个地区赋予一个自然环境致灾等级,分别用“轻灾”“中灾”“重灾”“特重灾”来表示对电网抗灾性影响的严重程度。该等级是一个考虑当地地质、气象等多种自然条件的综合性指标。结合相关专家的建议,对其各项特征进行编码。针对以下4 种自然属性提取各个地区的灾害信息:
(1)地质条件指对该地区的地势地形、土壤条件影响电网抗灾的描述。同样的气象条件下,地势高的电网受风灾、雷灾的影响更大;土壤质地疏松的地方更容易发生倒杆等。因此,地质条件是致灾因子中很重要的一项,其描述可为“地质条件适宜”“地质条件合格”“地质条件不适宜”等。
(2)风灾情况指对该地区风灾影响电网抗灾的描述。风灾可导致倒杆、断线等,长期处于强风地段的电网线路易发生磨损,受外界因素影响发生故障的概率更高。对风灾情况的描述可以根据当地风区的划分描述为“强风区”“大风区”“微风区”等。
(3)雷灾情况指对该地区雷灾影响电网抗灾的描述。雷灾可在线路上产生过电压导致线路跳闸,也有可能因雷电流过大而烧毁电网设备。对雷灾情况的描述可根据当地年均雷暴日、落雷密度描述为“强雷区”“多雷区”“中雷区”等。
(4)洪灾情况指对该地区洪涝灾害影响电网抗灾的描述。洪涝灾害主要影响地质环境,比如因土壤疏松而发生倒杆;大雨也会加重绝缘子闪络,引发线路跳闸等。对洪涝灾害的描述可根据当地的最高日降雨量、平均日降雨量分为“严重洪灾区”“中等洪灾区”“轻微洪灾区”等。
对上述4 种自然灾害致灾属性进行合理量化,为各项属性编制特征区分码。以地质条件为例,分为“地质条件适宜”“地质条件合格”“地质条件不适宜”3 级,分别编码为0,1,2,其余3 个属性亦然。
现有的聚类方法主要包括模糊聚类、灰色聚类等聚类分级方法,然而它们都离不开人为的参数干预,并且其应用背景都是灾害记录已过度量化的情况。因此本文选用蚁群聚类算法提取各个地区的灾害信息,从而有效减免灾害分级流程中主观因素的介入。
2.2 蚁群聚类算法
2.2.1 数据预处理
为改善因数据缺失导致数据聚合性差的问题, 对所有数据进行归一化预处理。设第n 个灾害的第i 个属性的初始值为预处理后变为zni:
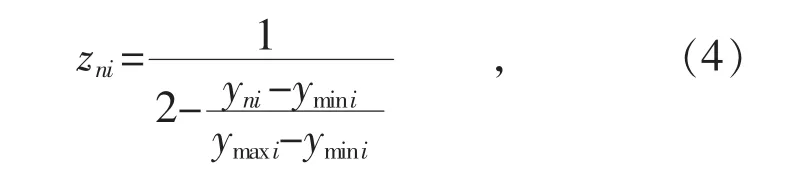
式中:ymaxi,ymini分别为灾害数据集合S 中第i 个属性的最大值和最小值。
2.2.2 聚类算法
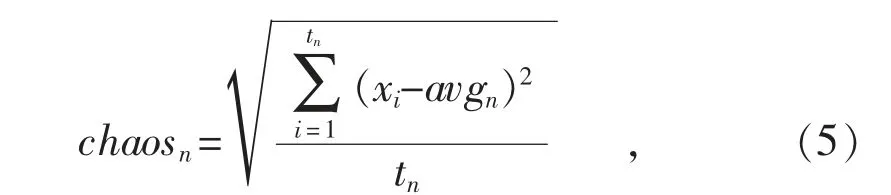
式中:xi表示第n 组中第i 条数据各属性的平方和;avgn表示第n 组各xi的平均值;tn表示第n个组的大小。
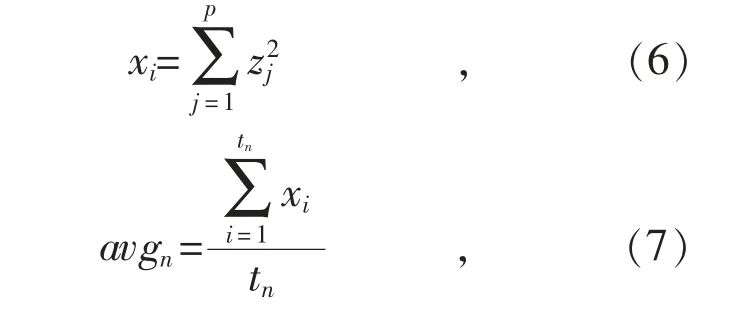
式中:zj表示第n 组的第j 条数据;p 表示第n 组数据的数量。
以各组chaosn值为依据,采用赌轮选择法[15]选一个出数数组。计算该数组中每个数据对其混乱度的影响,记作f。数据的f 值越大,则其被选中的概率越大。

定义similarityn(n∈[1,k])表示所选数据与各个数组的拟合度:
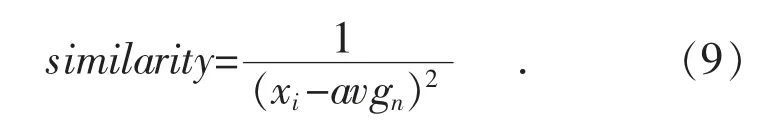
依据各组不同similarity 值采用赌轮选择法选出一个入数数组,将选出的数据放入此数组。
由于出数数组、数据、入数数组的选择都具有随机性,所以每次运行的结果都有多种可能。为保证算法的收敛性,采用fitness 来表示每种整理方法的质量:
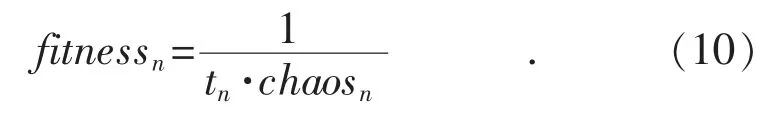
循环式(4)到式(9),当每次选出的数据一直被放回原数组,即聚类结果不再变化时,可根据各组聚类中心的大小顺序把各组数据划分为“轻灾、中灾、重灾、特重灾”。
2.3 灾害等级与抗灾建设成本
每个地区的灾害等级直接影响修建电网的成本,灾害等级越高,修建电网的抗灾建设成本越高。根据聚类结果,按照每类中心向量确定“轻灾、中灾、重灾、特重灾”对应的防灾建设方案,如最小档距、避雷器间隙,杆塔材质等。计算4 个等级建设同样规模电网的成本倍数关系,以轻灾为1,记中灾成本系数为α,重灾成本系数为β,特重灾成本系数为γ。在进行抗灾网架规划时,其成本需结合建设地的灾害等级乘以相应系数。
3 基于Steiner 树的抗灾型网架规划方法
3.1 基于灾害地图的抗灾型网架模型
对于防灾型配电网网架规划问题,可以采用前文所述增加中间节点的方法。网架建设成本中所增加的节点成本包括节点处杆塔的建设成本和杆塔建设处的受灾风险。而节点处杆塔的受灾风险可以使用权重系数归类到节点处杆塔的建设成本中,根据前文所述,对受灾风险大的地区,为达到抗灾的目标,其线路和杆塔的建设成本较高。通过查阅灾害地图,就可以得出不同位置节点处杆塔的建设成本参数,作为规划中的一个变量,由此得到基于灾害地图的抗灾型网架规划的数学模型:
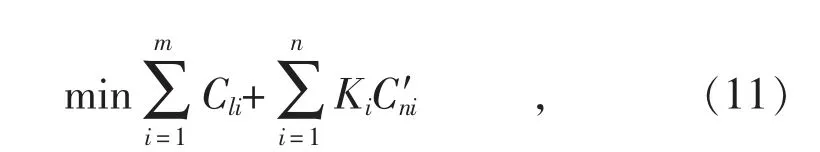
式中:Cli为线路的建设成本;为杆塔的建设成本;Ki为杆塔建设时的灾害成本系数,与其所在地区的灾害等级有关。
3.2 求解Steiner 最小树的方法
智能优化算法常被用于求解Steiner 最小树问题以及配电网规划问题[16-23],本文采用以最小生成树为基础的启发式算法——模拟退火算法[24]来求解抗灾型网架Steiner 最小树问题。模拟退火算法求解Steiner 最小树问题时计算量较小[25],能够有效跳出局部最优解的范畴,同时具有较快的运行速度,可满足工程实际需要。
在本文所述的规划问题中,原始点集包含负荷点集和变电站点集,共有n 个节点,采用模拟退火算法求解需要4 个步骤:
第一步:原始点集的预处理。根据Steiner 最小树的性质,待求的中间节点在原始点集所构成的凸包内,因此由原始点集的坐标位置可确定一个矩形区域(maxx,maxy分别为矩形的长和宽),划定Steiner 点搜索的可行区域;接着将上述区域等分成个网格:
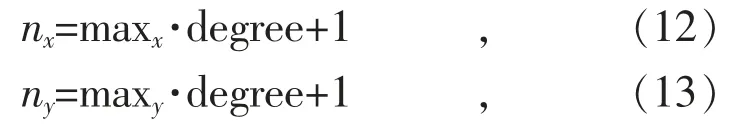
式中:degree 为网格细分倍数,取任意正整数,所有节点都放在网格顶点上。
第二步:初始化中间节点处杆塔的建设成本矩阵,杆塔的建设成本与节点所处位置的受灾风险有关。
第三步:采用模拟退火算法求解上述Steiner最小树问题。先对由原始点集构成的图计算最小生成树,得到初始配电网网架结构,并计算目标函数值,更新目标函数值记忆变量;随后开始模拟退火算法的迭代,在不同温度下对现有m 个中间节点进行多次如下操作,直至达到此温度下的平衡状态,再缓慢降温。
具体的操作选择如下:
(1)加入r 个新Steiner 点(r+m≤n-2)。
(2)删除r 个已存在Steiner 点(m-r≥0)。
(3)逐个移动m 个Steiner 点至各自邻域的任一“允许”位置。
由n+m 个点构造完全图,边长即为两点间的权重;计算此时的目标函数值(new_result),并令ΔW=new_result-last_result。结合配电网网架规划约束条件,判断此网架结构是否满足约束,若不满足则拒绝新解;若满足则进一步判断ΔW<0是否成立,成立则接受新解;否则依概率min{1,e-ΔW/tk}>random[0,1]接受新解,其中random[0,1]指[0,1]间的随机数。
第四步:对最后得到的可行解计算目标函数值,得到采用此网架规划方案的总费用,并记录此费用支出及其对应的配电网网架规划布局图,以此作为本规划问题的最优解。输出总费用最少的配电网网架规划布局网络图,结合配电网网架规划节点选址的需求,根据实际地理位置和中间节点的建造要求进行局部调整。
4 算例分析
采用Java 语言编程实现上述基于模拟退火算法,完成Steiner 最小树问题的求解。 对文献[27]中编号为102 的变电站所供电的子网进行网架规划,原网架有20 个负荷节点和1 个变电站节点,如图2 所示。首先对负荷节点和变电站节点构成的完全图计算最小生成树,进而得到不考虑增加中间节点的最优网架结构,作为算例分析的基准对比组。图2 中P1 点为变电站节点,以P1点为坐标原点,表1 给出了各负荷点的坐标和负荷需求,表2 给出了待建变电站的坐标。根据2.3所述算法得到电网所在地区不同区域的抗灾成本系数:轻灾成本系数为1.0,中灾成本系数为2.0,重灾成本系数为3.0,特重灾成本系数为6.0。
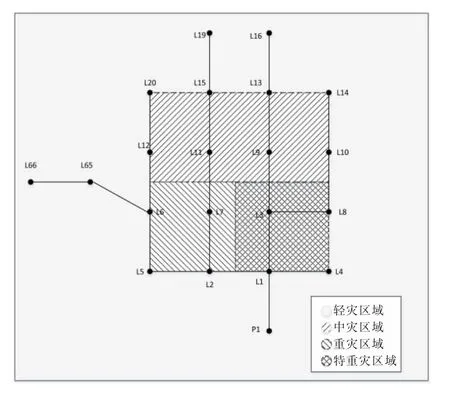
图2 传统方法网架规划结果
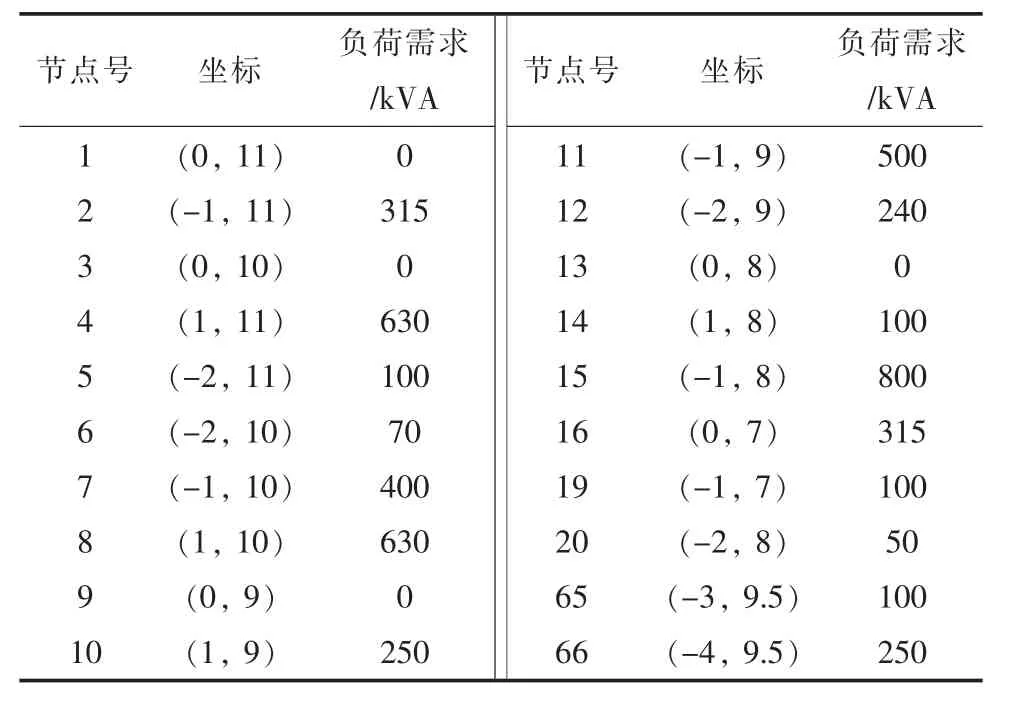
表1 各负荷点的坐标和负荷需求

表2 待建变电站位置
配电网络基本参数如下:额定电压10 kV,功率因数取0.95,等年值投资回收系数ω=0.155。馈线采用LGJQ-2×300 分裂导线,回路数a 取3,导线电阻率为31.5×10-8Ω·m,单位长度线路阻抗为5.25×10-5Ω/m,单位长度线路建设费用β1取50 万元/km。 一座变电站的建设费用取100 万元,中间节点的建设基准费用β1取0.5 万元,实际建设费用等于基准建设费用乘以建设地点的权重系数。
经过程序优化得到的新配电网网架如图3 所示,其中▲代表新增的中间节点,也就是Steiner点。优化前后的目标函数值如表3 所示。可以发现,本文所述算法求解Steiner 树的收敛速度较快,总的迭代次数较少,并且增加中间节点能够使配电网网架规划的目标函数值更小、总费用更优,有效降低了总体费用。
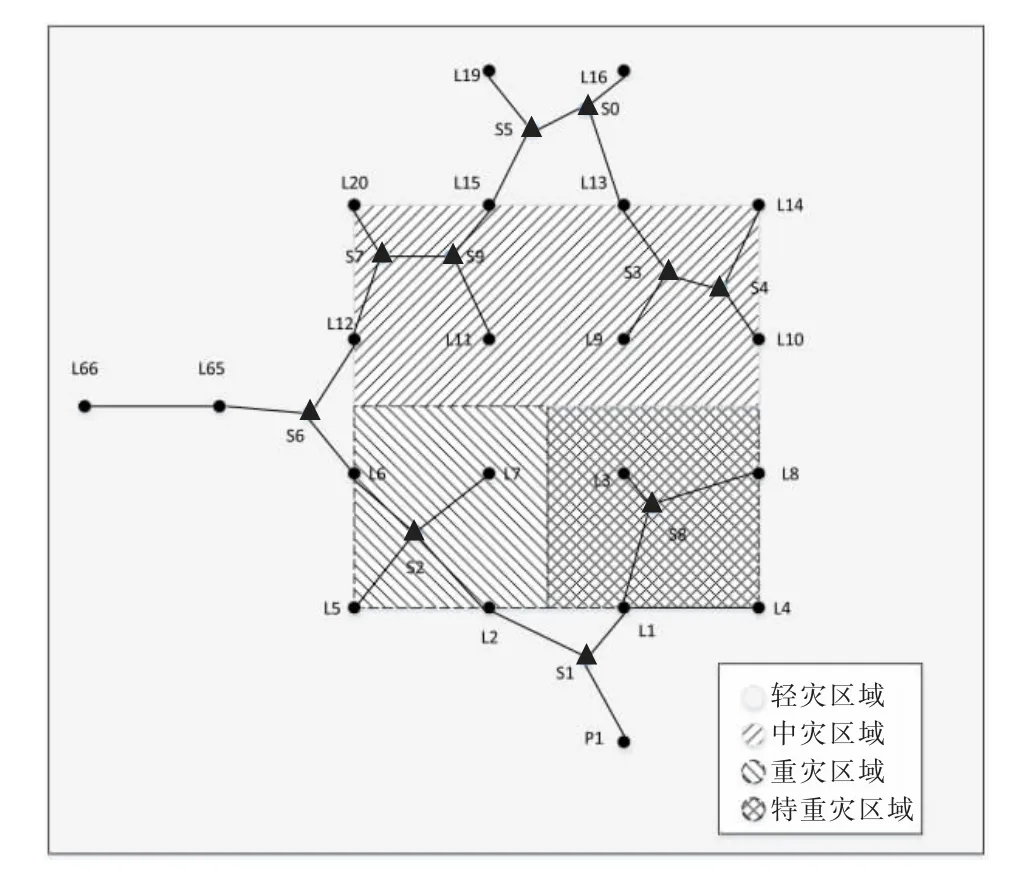
图3 本文方法网架规划结果

表3 考虑中间节点前后网架规划的总费用
5 结语
本文提出了一种基于灾害地图的配电网网架规划方法,该方法将网架规划问题转换成Steiner树模型,通过灾害地图求得增加中间节点的建设成本,求解得到配电网网架结构,能够适应对配电网辐射状运行的要求,同时考虑了电源负载量、潮流约束、馈线载流量等约束条件。所提方法通过增加中间节点减少配电网网架线路总长度,使得配电网网架规划方法更加灵活,增大了搜索到全局最优解的概率,能够更有效地实现配电网的优化规划。算例表明,基于本文方法得到的配电网网架建设总费用更低,使得配电网网架规划更经济。对于更大规模配电网的规划问题,后续研究可以考虑采用更高效的算法加快速度。
