计及负荷精细化建模的主动配电网双层规划模型
2019-07-10段登伟
罗 扬,段登伟,苏 鹏,韦 炜
(国网成都供电公司,成都 610041)
0 引言
现阶段我国能源结构仍以不可再生的化石燃料资源为主,能源短缺和环境污染问题已成为燃眉之急[1-3]。因此,低污染、灵活方便、高可靠性的DG(分布式电源)的有效推广与利用受到了越来越多的关注[4-5]。但传统配电网受限于其被动控制方式,难以应对具有间歇性[6]、波动性[7]特征的分布式电源所带来的一系列问题,无论是配电网规划还是主动配电网规划,截至目前,对配电网规划的文献大多集中在解决某些局部问题上。然而,未来主动配电网中必然存在较多的分布式能源,因此,对如何协调各类资源、实现资源的高效利用展开研究具有重要意义。
通常配电网规划多采用恒功率负荷模型,忽略了负荷的电压静特性。这类简化处理方法无法精确表征不同类型负荷的真实需求,文献[8-9]以恒定功率负荷作为配电网规划的重要组成部分,提出合理的配电网规划模型,但所涉及的负荷模型较为粗糙,导致系统分析结果过于乐观或悲观。因此在未来配电网规划建模中有必要考虑负荷的电压静特性,便于规划运行人员对负荷类型构成进行直观掌控,通过数值方法进行快速求解。
另外,在主动配电网规划中考虑需求响应的必要性日益显现。文献[10]表明,在主动配电网系统规划中,考虑对DR(需求响应)进行建模可以有效解决负荷波动过大所带来的系统运行安全稳定问题[11-12]。需求响应根据负荷响应机制分为:基于激励的需求响应和基于价格的需求响应[13-14]。与基于价格的响应负荷相比,基于激励的响应负荷更易在配电网规划中实施[15],所以本文的需求响应模型采用可调度响应负荷。
主动配电网规划数学优化模型是一个包含投资层和运行层的双层优化问题[16]。将投资层和运行层进行分开求解的传统方法,容易导致上层规划的收敛性较差,且计算时间较长,因此当前迫切需要深入探索投资层和运行层的统一建模求解方法,从而较快获得整个主动配电网规划模型的全局最优解。 因此本文通过关联运行层和投资层,将原模型转化为单层混合整数二阶锥规划,采用CPLEX 算法包进行快速求解,最后,以改进的IEEE 33 节点配电系统进行算例分析验证。
1 主动配电网双层规划模型
本文以DG 数目、馈线升级类型和DR 容量为上层决策内容,同时基于上层规划结果,结合DG 和负荷潮流特性,以DG 出力、主网购电量和DR 功率为下层决策内容,构建主动配电网双层规划模型,其目标函数主要包含投资成本(Cinv)和运行成本(Cope)。约束条件包含投资约束和稳态模拟运行约束。根据配电网规划模型特点,设备投资决策变量和模拟运行变量可以进行分离,因此主动配电网分层规划模型可以表示为:
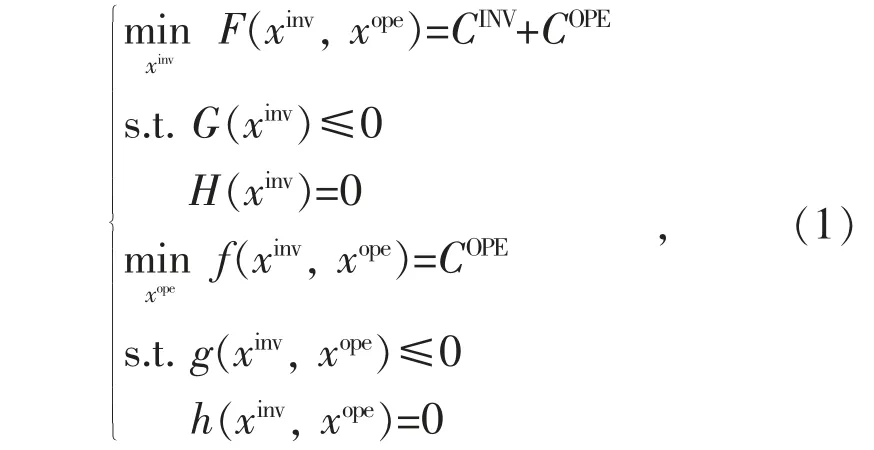
式中:G(.)和H(.)为上层约束,即投资约束,包含设备投资约束和设备安装数量等;g(.)和h(.)为下层约束,即运行模拟约束。该模型为单向双层模型,即上层模型为下层传递状态变量,而下层变量决策和影响上层,仅仅是通过添加运行成本到上层约束中体现。
1.1 规划层模型及约束条件
1.1.1 规划层模型
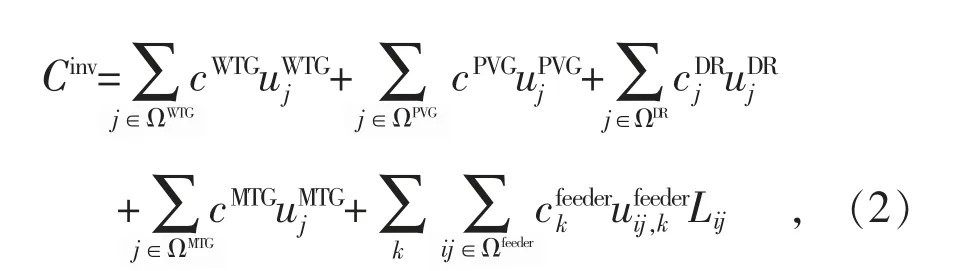
式中:Cinv为折算后规划方案投资费用;ΩDR,ΩWTG,ΩPVG,ΩMTG和Ωfeeder分别为DR,WTG(风电机组)、PVG(光伏机组)、MTG(微型燃气轮机组)和馈线的候选集合;分别为其单位投资成本系数;为DR 容量;分别为其安装数量。
1.1.2 投资约束
投资约束包括设备投资约束和DR 容量约束,设备投资约束为配电网中各设备投资数量约束,DR 容量约束为电网公司签订的DR 容量限制,具体可参考文献[15]。
1.2 运行层模型及约束条件
1.2.1 运行层模型

式中:Cope为运行成本;和分别为MTG 发电成本价格、弃电惩罚价格、主网购电价格、网损价格和DR 价格;分别为WTG,PVG 发电预测功率;分别为WTG,PVG 发电有功注入功率。
1.2.2 运行约束
(1)DG 出力约束

(2)弃电约束

式中:μWTG,μPVG分别为WTG,PVG 允许弃风、弃光比例;分别为各典型日下WTG,PVG发电最大值。
(3)潮流运行约束
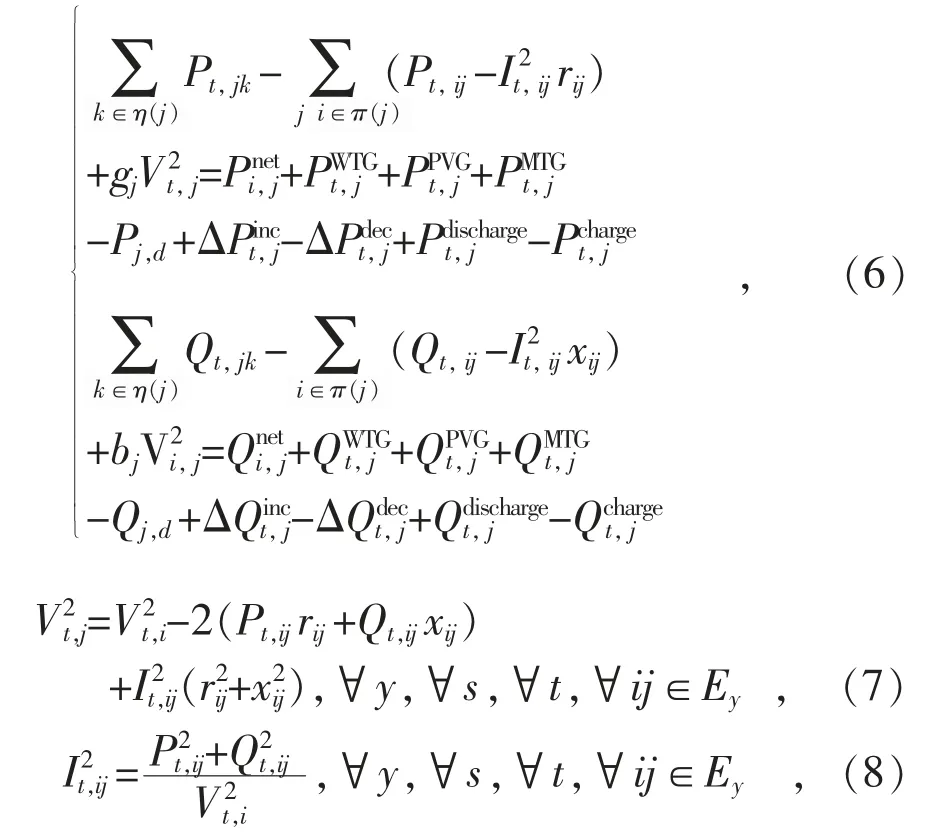
式中:xij为支路ij 的电抗;Pt,ij,Qt,ij分别为支路ij的有功、无功功率。
(4)负荷精细化约束
综合负荷模型即负荷精细化模型,便于更直观地控制荷载类型。该模型可表达为负荷功率与电压之间的关系,其一般形式如下:

2 模型求解
由文献[15]知,将投资层变量与运行层参数相关联。 模型(1)-(11)最终可表达双层优化模式。本文对风机和光伏机组进行投资运行关联,对于WTG 和PVG 约束而言,弃风、弃光约束的各个变量应与WTG 和PVG 决策变量(即与WTG和PVG 安装数量)进行耦合。
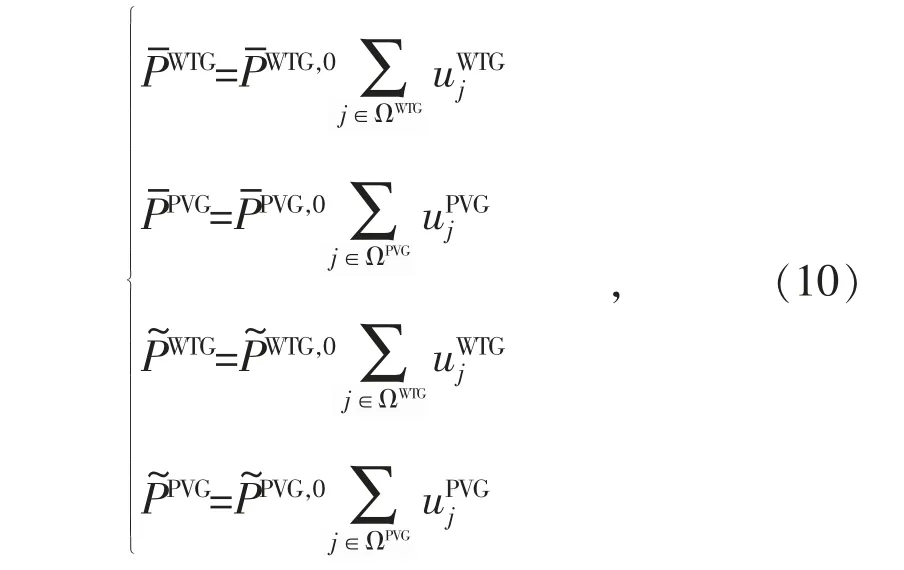
由于潮流模型(6-8)和综合负荷模型(9)为非线性,且通过投资运行约束关联后,将产生更多的非线性项,从而增加模型求解的难度,因此需对其进行线性化处理
2.1 潮流模型的非线性处理
本文利用二阶锥技术对潮流模型(6-8)进一步松弛,将混合整数非线性模型转化为二阶锥规划模型,引入中间变量和则潮流模型可转化为:
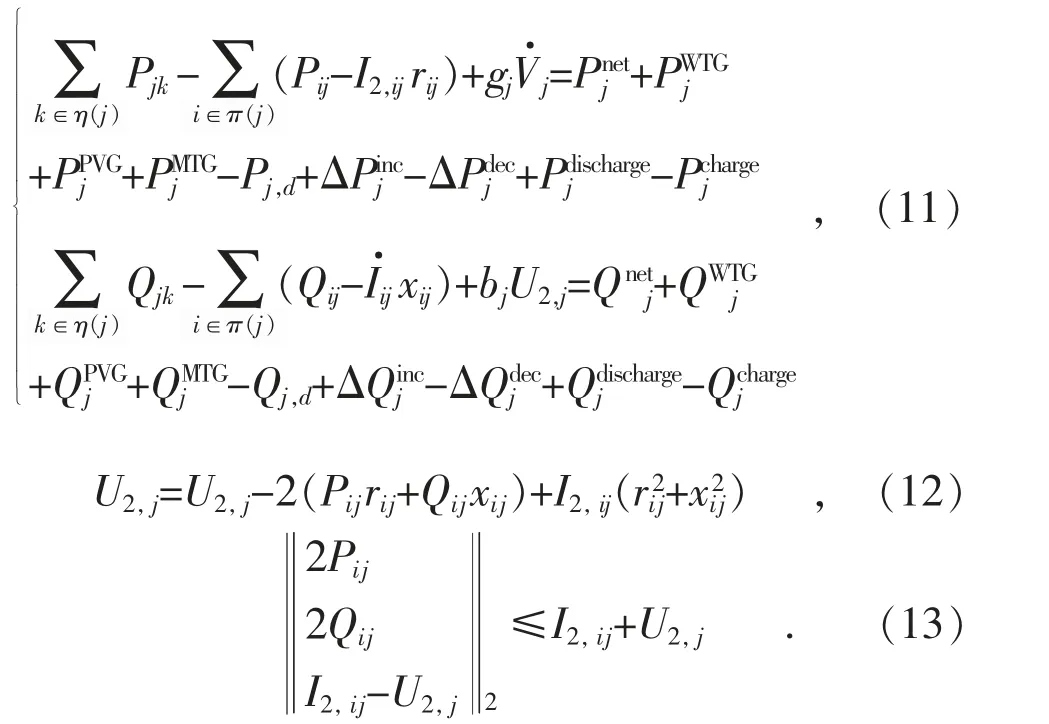
2.2 负荷精细化模型线性化处理
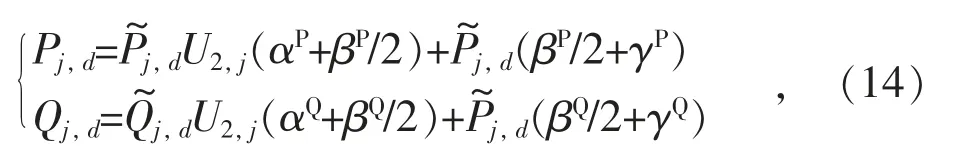


对于式(16)存在的双线性项λj,sU2,j,可采用big-M 方法处理,令并加约束(17):

式中:M 为一个较大的常数。储能设备中所涉及的双线性项处理也类似。通过式(10-17),系统模型转变为单层混合整数二阶锥规划问题。
3 算例分析
3.1 算例参数
本文采用修改的IEEE 33 节点算例进行分析,其网络结构见图1,具体的数据参数参考文献[17]。弃风、弃光、失负荷惩罚成本均取5 000$/MWh,为了模型的精确性,选单位网损价格为500$/MWh,各时段电价见图2。各个DG 参数见表1,线路型号见表2,基于MATLAB R2016a 软件平台,采用12.6 版本的CPLEX 算法包,对系统进行仿真分析。
3.2 算例结果
3.2.1 规划方案分析
本文对3 种情形进行研究。情形1:考虑负荷精细化和DR;情形2:考虑负荷精细化,忽略DR;情形3,忽略负荷精细化,考虑DR。规划结果如表3 所示。

图1 电价曲线
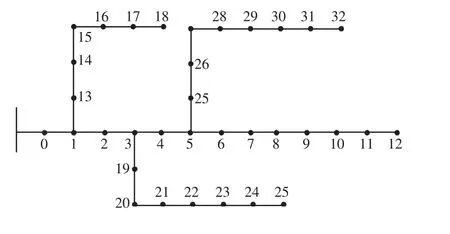
图2 33 节点AND 系统结构
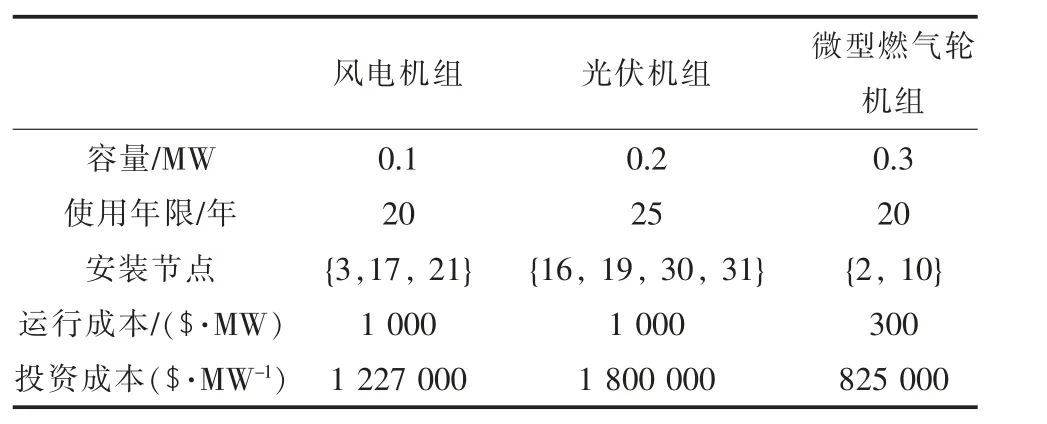
表1 不同类型分布式电源相关参数
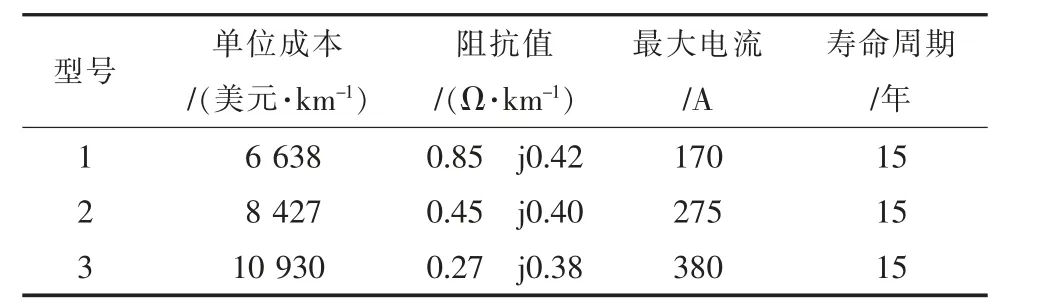
表2 线路待选型号参数

表3 规划结果
其中情形2 中各DG 投资数量最大,情形1最小。这说明在主动配电网中考虑负荷精细化模型和需求响应,能够有效地降低各个设备的投资。
3.2.2 节点电压
计算考虑负荷精细化后的各节点电压,其分布如图3 所示。

图3 电压分布
由图3 可知:各个节点的电压绝大部分都大于1.0 p.u.,即考虑负荷精细化后,系统电压稳定性增强,且系统的负荷需求相应提高。
3.2.3 算法实用性分析
为验证本文算法的求解效率,分别采用智能算法和传统数值算法进行对比分析,如表4 所示。原规划模型本质上为MINLP(混合整数非线性规划)问题,从表4 可以看出,由Bonmin 算法求解该问题,无法获得最优解,而采用遗传算法求解耗时较长,且求解困难,但将其转化MISOCP(混合整数二阶锥规化)后,求解效率大大提高。
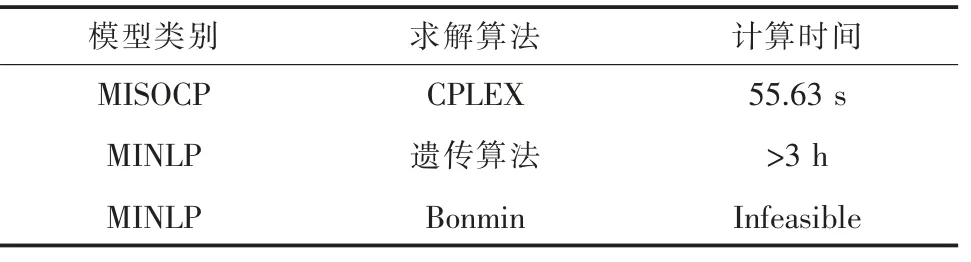
表4 不同算法下的求解信息对比

图4 为各时段各支路下的误差散点图。显然凸松弛之后的误差最大值非常小,为10-4量级左右,明显小于潮流方程收敛判据等要求,这表明了本文的松弛是严格而准确的。

图4 各时段各支路下的误差散点图
4 结论
本文构建了考虑DG 和负荷精细化建模的配电网双层协同规划模型,并通过投资运行耦合关联和线性化等值处理,将其转化为混合整数二阶锥规划模型进行求解,结果表明采用负荷的精细化模型,能为主动配电网协同规划提供一定的参考。同时,系统电压更趋于稳定,提高配电网系统的供电可靠性,使得上下层相互影响作用,得到更优的规划方案,满足规划要求。此外通过对上下层变量关联建模和线性等值处理,引入二阶锥松弛,将原模型转化为单层混合整数线性规划,大大提高了求解速度和计算精度。
