超疏水表面对湍流边界层相干结构影响的TRPIV实验研究

2019-07-10刘铁峰王鑫蔚唐湛棋

实验流体力学 2019年3期

刘铁峰, 王鑫蔚, 唐湛棋,2, 姜楠,2,*

(1. 天津大学机械工程学院, 天津 300354; 2. 天津市现代工程力学重点实验室, 天津 300354)

0 引言

当液滴处于某一固体表面，若其静态接触角大于150°、滚动角小于10°，则称该表面为超疏水表面[1]。超疏水表面具有很好的自清洁功能[2-3]。自然界中存在大量的超疏水表面，最常见的有荷叶、水稻等植物叶片的表面。近年来，电子显微技术的飞速发展推进了相关领域学者对超疏水表面的研究：1997年，Barthlott等[4]观察到植物叶片表面存在着微米级凸起和纳米级蜡状物，且发现二者的共同作用是导致植物叶片表面产生疏水性的主要原因。在此之后，一些研究者逐渐开始人工制备超疏水材料并进行了一系列研究，发现超疏水材料能够有效减小液体与固体壁面之间的摩擦阻力，可广泛应用于水面、水下航行工具表面，以达到节约能源、提高航速的目的。由此可见，超疏水材料在工业与国防领域具有巨大的发展潜力与应用前景，得到了广泛关注[5-7]。

在超疏水表面湍流减阻方面，Daniello等[8]进行了微槽道湍流压降实验，在其给定的几个中等雷诺数范围内，发现减阻效果与雷诺数呈正相关。Min和Kim[9]采用DNS方法研究了壁面滑移对减阻效果的影响，发现流向滑移能够减小壁面摩擦阻力，而展向滑移会使阻力增加，2种滑移方向的综合作用决定了材料的减阻效果。Park等[10]的DNS结果表明：当内尺度无量纲流向滑移长度λ+达到黏性长度δv量级时，减阻效果开始发生，且与λ+呈正相关。Bidkar等[11]的研究表明：当内尺度无量纲粗糙度k+小于0.5时，减阻效果较为明显。Busse和Sandham[12]的结果也表明，当k+大于5时，并没有得到减阻的效果。Park等[13]通过实验的方法得到了减阻效果与壁面微结构的气含率密切相关。宋保维[14]和段慧玲[15]等也得到了相似的结果，并对超疏水表面的气液稳定性研究进行了总结。田海平和王二丹等[16-18]的实验结果表明，超疏水壁面能够削弱猝发事件的强度及低速条带的尺度。苏健等[19]的研究结果表明，超疏水壁面减阻效果的发生与逆向涡的存在密切相关。

对超疏水表面湍流减阻的研究，主要从表面微观结构和壁面滑移理论等方面进行，重点关心减阻效果；而从实验角度研究超疏水表面对湍流边界层中相干结构的影响，并从该角度解释其减阻机理的文章比较少。研究表明，湍流边界层中存在着大量相干结构，对湍流的产生、维持、发展和演化起到重要作用，同时也为湍流控制技术提供了切入点。尤其是在湍流边界层的对数律层中存在的大量发卡涡及由多个发卡涡所组成的涡包结构，可以诱导产生连续的喷射和扫掠事件，在其下方形成连续的低速流体，对湍流边界层中壁面摩擦阻力的产生贡献很大[20-26]。研究超疏水表面对相干结构的影响，为揭示超疏水表面减阻机理提供了新的思路。

本文利用高时间分辨率粒子图像测速技术，得到2种表面瞬时速度矢量场的大样本时间序列，对比2种表面的平均速度剖面和湍流度。选取3个法向高度，采用二维空间两点相关函数的方法计算2种表面流向脉动速度的相关系数，定义并对比相干结构的流向尺度。以λci准则检测到的发卡涡头作为条件事件，通过线性随机估计方法分别对条件事件周围的脉动场进行计算，对比同一法向高度2种湍流边界层中发卡涡及涡包结构的异同，揭示超疏水壁面的湍流减阻机理。

1 实验装置及参数

实验在天津大学流体力学实验室低速循环式水槽中进行。水槽实验段尺寸530cm×25cm×38cm，自由来流背景湍流度小于0.7%。通过调节与步进电机泵相对应的变频器，可以控制水槽自由来流的速度。实验用大平板尺寸为240.0cm×38.0cm×1.5cm，前缘为8∶1椭圆修形，距前缘190cm处留有凹槽，用于镶嵌尺寸为28.0cm×28.0cm×1.5cm的亲水平板及超疏水平板模型。距大平板前缘8cm处装有直径6mm的拌线，确保湍流边界层在测量区域处于充分发展状态,如图1所示。实验所用的超疏水平板模型由清华大学姚朝辉课题组[27-28]提供，其表面具有微纳二级结构，静态接触角为161.0°，滚动角为0.9°。亲水平板为有机玻璃板，用于对比研究(Hydrophilic surfaces表示亲水表面；Superhydrophobic surfaces表示超疏水表面)。

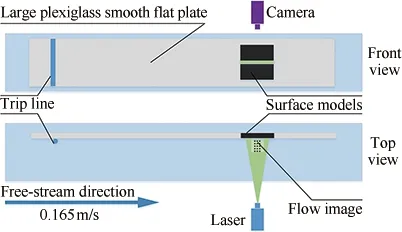
图1 实验装置示意图

实验用示踪粒子为直径20μm的空心玻璃微珠，粒子密度1.03g/cm3。实验时自由来流速度0.165m/s，水温21℃，对应水的密度为998kg/m3，动力黏度系数1.003×10-3kg/(m·s)。高速相机分辨率1280pixel×1024pixel，采样频率500Hz，相邻两帧脉冲时间间隔2000μs，单帧曝光时间1500μs。图像视野实际尺寸为56.6mm×45.1mm，采用自适应互相关算法，查询窗口大小为32pixel×32pixel，窗口重叠率75%，得到瞬时速度场6547个，每个瞬时速度场包括157×125个速度矢量，其流向和法向相邻矢量间实际距离为0.358mm。

2 湍流基本统计量分析

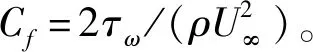
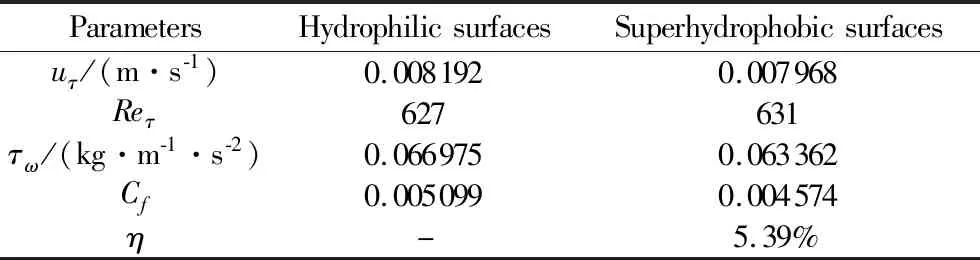
表1 基本湍流减阻参数Table 1 Basic turbulent drag reduction parameters

图2为2种壁面的内尺度无量纲平均速度剖面曲线。横轴y+=yuτ/ν，纵轴u+=u/uτ，其中ν为实验用水的运动黏度系数,u为流向速度。从图中可以看出，在同一法向高度，超疏水壁面的内尺度无量纲平均速度大于亲水壁面。超疏水壁面表现为缓冲层增厚，对数律层外移，其整个平均速度剖面略向上偏移，符合湍流边界层减阻的典型特征。图3为2种壁面湍流度的流法向分量分布曲线(图中u′、v′分别为流向脉动速度和法向脉动速度)，可以看出，超疏水壁面主要抑制了流体质点的流向脉动，对法向脉动几乎无影响。

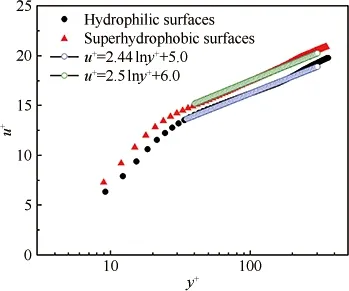
图2 平均速度剖面

图3 湍流度流法向分量剖面

3 2种壁面相干结构的对比研究

本节先采用二维空间两点相关函数的方法计算2种壁面流体质点流向脉动速度的相关性，并对比相干结构的流向尺度。进一步采用线性随机估计的方法计算2种表面发卡涡头周围脉动速度场的分布，分析导致流体质点流向脉动速度相关性改变的原因，并结合超疏水表面的减阻现象进行讨论。

3.1 二维空间两点相关函数的计算方法

二维空间两点相关系数可以确切地表达流法向平面内流体质点间的关联程度，是研究湍流相干结构的经典方法[30]。本节采用流向脉动速度的相关系数来提取2种表面工况下壁湍流中的相干结构，具体数学表达形式如下：

(1)

式中，Ruu(Δx,y,yref)表示流法向平面内两流体质点间流向脉动速度的相关系数，yref为法向参考位置。y∈[0，ly]，表示流体质点的法向位置；Δx∈[-lx/2，lx/2]，表示两流体质点间的流向间距，其中lx、ly分别取120、30个网格点。相邻网格间距对应到2种壁面分别为3.06(亲水平板)和2.98(超疏水平板)个黏性长度。〈u′(x,yref)u′(x+Δx,y)〉表示位于(x,yref)与(x+Δx,y)处两流体质点间流向脉动速度的相关函数。σu′(yref)表示法向参考位置yref处流向脉动速度的均方根值，σu′(y)表示法向位置y处流向脉动速度的均方根值。

3.2 二维空间两点相关函数的计算结果

本节对比了2种表面下不同法向参考位置处流向脉动速度空间两点相关系数的计算结果。所选法向参考位置处的y+对应于亲水平板和超疏水平板分别为30.59和29.76，得到的结果如图4所示。

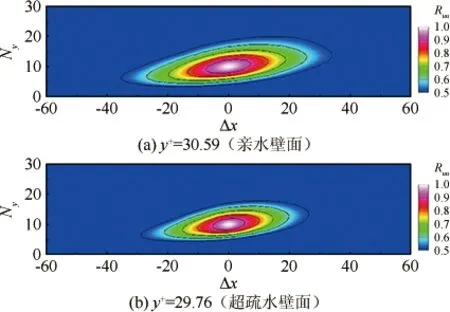
图4 空间两点相关系数计算结果

图4表示空间两点流向脉动速度的相关系数在不同流向和法向空间延迟Δx、Δy下的等值线云图分布。其中横坐标Δx在参考点右为正，在其左为负；纵坐标Ny表示距离壁面法向高度(横纵坐标均为网格点数，即用横纵网格大小进行了无量纲化)。

由图4可以看出，在流法向平面内，流向脉动速度的空间两点相关系数等值线呈现出类似椭圆状的外形特征。通过圆锥曲线方程对相关系数等值线附近的边界点进行拟合，并采用最小二乘法确定曲线方程的系数，可以得到对应的椭圆方程。考虑到相干性的大小及椭圆拟合的规则性，本文选取相关系数为0.5的等值线坐标点作为拟合参考点，其中数据点选取的拟合误差为±0.008。定义椭圆边界在水平方向的投影为相干结构的流向尺度，可以定量地得到超疏水壁面对相干结构的影响。

图5给出了近壁区2种表面相干结构流向尺度随法向位置变化的关系曲线。其中相干结构的流向尺度均采用各自对应的黏性长度来衡量。对比发现：相对于亲水壁面，超疏水壁面中相干结构的流向尺度明显减小。前文提及发卡涡包结构在湍流边界层中占有重要地位，且周围流体具有较好的相关性，则流体质点间流向脉动速度相关性的变化，定与发卡涡及发卡涡包等结构的改变有着密切的联系。因此，在下一节中，采用线性随机估计的方法对湍流边界层中的发卡涡及涡包结构进行提取，进一步研究超疏水壁面对发卡涡及涡包结构的影响，结合超疏水壁面的减阻现象进行讨论。

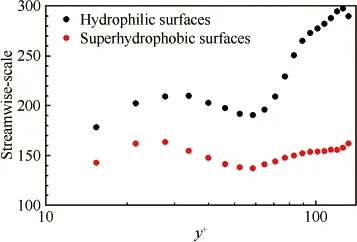
图5 相干结构的流向尺度

3.3 线性随机估计的计算方法

线性随机估计同样是提取湍流相干结构的一种统计方法，其特点是通过给定条件事件，能够得到其周围与之相关物理量的最可能分布情况，可以在特定条件下提取到与之对应的相干结构[31-33]。本节用到的线性随机估计数学表达形式如下：

(2)

定义旋转方向为顺时针的展向涡结构为顺向涡，其可以认为是发卡涡头在流法向平面内得到的截面，能够从侧面体现出发卡涡结构的基本特征。所以本文将检测到的顺向涡作为条件事件，采用线性随机估计的方法得到其周围脉动速度场的最可能分布情况，通过对比2种表面的顺向涡及发卡涡包结构的异同点，进一步阐述超疏水壁面对湍流中相干结构的影响。

对于涡旋的判定有多种检测方法[34]。作为一种最常用方法，λci准则能够准确识别流法向平面中展向涡结构的涡心位置，并且能够排除剪切层的干扰[21,35]。通过结合涡量符号，能够同时准确判定展向涡结构的旋转方向并提取到顺向涡。具体的数学表达形式如下：

Λci(x,y)=λci(x,y)sign(ω(x,y))

(3)

式中，λci(x,y)表示(x,y)处展向涡的强度，ω(x,y)表示对应的涡量值，sign表示涡量ω(x,y)所对应的符号。在实验测量和数据处理过程中存在背景噪声，为了避免背景噪声对计算结果产生影响，当检测点的Λci值小于-1倍的同一法向高度所有Λci的均方根值，且为周围8个点的极小值(包含检测点)时，提取对应的顺向涡结构[36-37]。对应检测函数的数学表达形式如下：

(4)

3.4 线性随机估计的计算结果

本节同样对比了2种表面3个法向参考位置处的线性随机估计结果。所选取的法向位置与上文相同，其y+值对应于亲水平板(超疏水平板)依次为30.59(29.76)、36.71(35.71)、42.83(41.66)，得到的结果如图6所示(横纵坐标轴同样均以相邻网格间距为单位长度)。

在图6中，横坐标Nx表示在条件平均区域内、以条件平均截取的图像最左边界为0时的流向相对坐标，用于表示相干结构的流向相对位置。纵坐标Ny表示距离壁面法向相对高度。

图6 线性随机估计结果

在图6(a)～(f)中，处于Nx=20所在竖直线上的实心黑点为条件事件的相位中心，即发卡涡的涡心位置。由图6可以得到基于顺向涡为条件事件、周围脉动速度矢量分布的统计平均结果。可以发现，矢量图呈现出很好的顺时针旋转趋势，且在每个发卡涡的上游和下游分布着明显的Q2(喷射)和Q4(扫掠)事件。在图6(a)、(c)所给出的亲水平板结果中，相位中心下游也能看到2个明显的发卡涡结构(其涡心以实心灰点标出)，但其旋转的规则性逐渐减弱，这是由于其位置与相位中心的距离增大所造成的。但图6(e)的结果相比于(a)和(c)不是特别明显，可能是由于法向位置的抬升、相邻发卡涡间距发生变化所致。由脉动速度矢量图的分布可知，在每个发卡涡的内部均表现为稳定的焦点结构，而在距离涡心上游和下游不远处，则由于相邻发卡涡之间Q2和Q4事件相遇，表现为鞍点结构。总体来说，图6中的每一个涡旋都呈现出1个稳定的焦点和2个鞍点结构。

由图6(a)、(c)可以看到，多个发卡涡前后有序排列，其所组成的连续结构即为Adrian等所提出的充斥于湍流边界层中的发卡涡包结构[21-22]。由于发卡涡产生于壁面，随着时间的推移在法向上逐渐抬升，导致位于下游的发卡涡法向位置略高于上游，所以在多个连续的发卡涡之间能够形成一个上扬的倾角[26,38]。图中用绿色点划线表示涡包与水平方向的夹角，在图6(a)、(c)、(e)所表示的亲水壁面中，由发卡涡组成的涡包结构与水平方向分别形成8.17°、8.23°和11.20°夹角，这与Christensen等的研究结果一致[33]。同时，涡包中多个发卡涡的连续作用，能够使每个发卡涡诱导产生的低速流体在涡包所形成的倾角下方连成一个整体，流体质点间呈现出很好的连贯性。

值得注意的是：分别对比图6(a)和(b)、(c)和(d)以及(e)和(f)，超疏水壁面在黑点所处相位中心处的发卡涡头强度小于亲水壁面。在云图中具体表现为相位中心上方淡白色区域与下方深蓝色区域面积略有减小，即超疏水壁面上方高速流体的扫掠和下方低速流体的喷射强度均略小于亲水壁面。另一方面，在超疏水壁面中，与条件事件中心相邻的下游发卡涡结构的法向位置明显高于亲水壁面，间距也大于亲水壁面(可以对比图6(a)和(b)，超疏水壁面体现出的涡包倾角大于亲水壁面)。而超疏水表面中单个发卡涡之间的这些变化，同时也导致了由多个发卡涡组成的有组织的涡包结构发生了改变：在图6(a)、(c)和(e)相同量级云图所表现的亲水壁面中，涡包下方黄绿色区域所表示的低速流体连接得较为完整，呈现为一个整体；而在图6(b)、(d)和(f)所示的超疏水壁面中，这种整体性被破坏，同时在低速流体区域，流体质点流向脉动速度的整体强度也明显小于亲水壁面，这与超疏水表面能够产生壁面滑移效应密切相关，有利于减小壁面摩擦阻力。超疏水壁面中相干结构的破坏，也很可能是导致第2节湍流基本统计量中流向湍流度降低的内在原因。而低速流体的连贯性减弱，也与采用空间两点相关函数方法得到的流向尺度减小的结果一致。