基于HPSO-BP神经网络融合的锂电池SOC预估研究＊

于仲安 褚彪 葛庭宇

（江西理工大学，赣州 341000）

主题词：荷电状态 磷酸铁锂电池 混合粒子群算法 BP神经网络

1 前言

动力电池荷电状态（State Of Charge，SOC）的预测在电池管理系统（Battery Management System，BMS）中具有极其重要的地位，准确预测电池SOC不仅能够提高电池系统的安全性，避免电池过充、过放，延长使用寿命，而且可以优化驾驶和提高电动汽车的使用性能[1]。目前主流的锂电池SOC估计方法有安时积分法、开路电压法、内阻法、卡尔曼滤波法、人工神经网络法等。这些方法都有各自的优缺点，通过一定的改进与联合，可以提高锂电池SOC的预测精度。文献[2]提出由标准卡尔曼滤波器和无味卡尔曼滤波器组成的双重过滤器，用以预测电池内部状态；文献[3]利用非线性预测滤波器（Nonlinear Predictive Filter，NPF）电荷估计方法，可以任意统计分布形态，准确估计电池的SOC；文献[4]提出一种基于改进滑模观测器的SOC估计算法，采用sigmoid函数代替传统滑模观测器中的符号函数，并对观测器中的模型参数进行在线更新，进一步消除参数变化带来的模型误差，从而提高估计精度；文献[5]提出基于递归非线性自回归（Nonlinear Autoregression with Exogenous，NARX）神经网络模型，利用闪电搜索算法（Lightning Search Algorithm，LSA）寻找输入延迟、反馈延迟和隐藏层神经元的最佳值，对锂离子电池进行了精确而可靠的SOC估计；刘艳丽等[6]提出有限差分扩展卡尔曼滤波算法，用于锂电池SOC的估算，取得了很好的精度；李哲等[7]通过修正初始SOC值，提高安时积分法的精度，对后续的SOC估算精度提高有很大的参考价值。

人工神经网络拥有强大的自学习能力，能够通过对训练样本数据的学习实现对输入、输出间内在规律的刻画，因此具有高度的非线性能力，此外，还拥有优秀的容错性和鲁棒性，非常适合应用于锂电池SOC的估算[8]。BP算法理论依据坚实、通用性好，至今仍是前向网络学习的主流算法，但其同时存在着本质缺点：容易陷入局部极小，收敛速度较慢，学习率不易选择。

遗传算法（Genetic Algorithm，GA）遵循“优胜劣汰，适者生存”原则，具有全局最优的特点。将遗传算法与BP网络结合起来形成GA-BP网络算法，可以克服BP算法陷入局部最优的缺点，提高网络稳定性。标准粒子群算法在基本粒子群算法的基础上引入了惯性权重w，适当选择w的大小可以使得算法具有广域搜索能力和局部搜索能力，然而依然避免不了陷入局部最小的问题[9-10]。

粒子群算法比较简便、易于实现，没有过多参数需要调整，本文采用HPSO-BP算法，将粒子群算法与遗传算法中的交叉变异思想结合起来，用于优化BP神经网络中的初始权值和阈值，可以提高收敛速度，克服易陷入局部极小的缺点。

2 基于BP神经网络的锂电池SOC预测模型

根据Kolmogorov定理，3层的前向网络在隐层神经元数目足够多的情况下，能够以任意精度对非线性函数进行映射。本文采用应用最为广泛的BP神经网络对锂离子电池SOC进行预测。将锂电池的工作电压U、工作电流I、内阻R、环境温度T作为电池SOC的影响因子，即SOC=f(V,I,R,T)。图1所示为BP神经网络SOC预测模型。

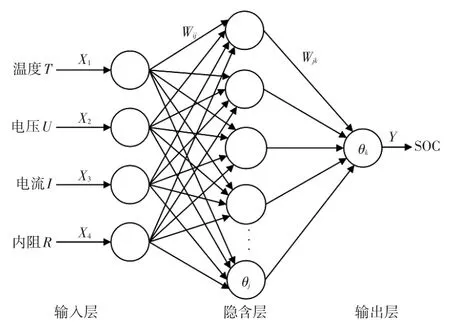
图1 基于BP神经网络的SOC预测模型

BP网络的输入矢量为[X1,X2,X3,X4]，网络输入层节点数n=4，电池SOC作为输出矢量[Y]，输出节点数为l=1，根据经验公式m=(n+l)0.5+a（a为[1,10]范围内的常数[11]），经过多次仿真试验，设m=12时，网络的误差精度更高，收敛速度也更快。网络激活函数选用tansig函数，性能函数选为均方误差性能函数（Mean Squared Error，MSE）。

3 混合粒子群算法优化BP神经网络

3.1 标准粒子群算法

粒子群优化（Particle Swarm Optimization，PSO）算法是由Eberhart博士和Kennedy博士于1995年提出的一类群智能随机优化算法，其思想源于对鸟群捕食行为的研究[12]。在粒子群算法中，每个粒子都代表着问题的一个潜在最优解，对应着适应度函数决定的适应度值，其大小决定着解的优劣程度。在每一次迭代中，粒子通过跟踪个体极值pbest和全局极值gbest更新自身的速度和位置。

粒子i的信息用D维向量表示，包括速度信息vi=(vi1,vi2,…,viD)T和位置信息xi=(xi1,xi2,…,xiD)T，速度和位置的更新公式分别为：

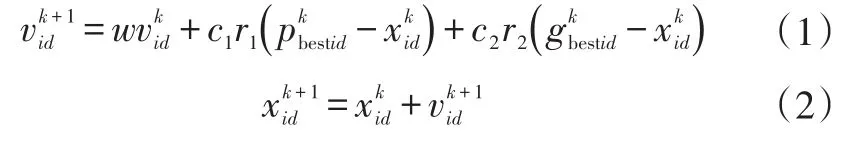
式中，d∈[1,D]为维数；w为惯性权重；k为当前迭代次数；c1、c2为学习因子或者加速系数，通常取为2；r1、r2为[1,0]区间内均匀分布的伪随机数。

惯性权重的大小决定了粒子对当前速度继承的多少，合理选择可使粒子具有均衡的探索能力（广域搜索能力）和开发能力（局部搜索能力），目前调整惯性权重w的策略有线性调整、模糊调整、随机调整等。模糊调整策略参数比较多，增加了算法的复杂度；随机调整策略在面临动态优化问题时，不能预测粒子群需要更好的探索能力还是开发能力；线性调整策略使算法前期具有全局搜索能力，后期具有局部搜索能力，并且调整策略简单易行，符合实际优化问题的一般策略。故本文采用线性调整策略：

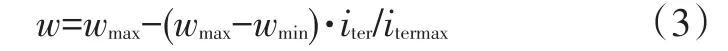
式中，wmax、wmin分别为惯性权重的最大值和最小值；itermax、iter分别为最大迭代次数和当前迭代次数。

一般将惯性权重初始化为0.9，随着迭代次数的增加，w线性递减至0.4。

3.2 混合粒子群算法

粒子群算法虽然具有收敛速度快、操作简单等优点，但是随着迭代次数的增加，种群达到收敛时，个体粒子越来越相似，使得粒子群很可能陷入局部最优困境。鉴于此，本文将遗传算法中的交叉、变异操作融入粒子群算法中，交叉操作体现粒子群算法中信息交换的思想，变异操作不但可以维持种群的多样性，而且能够减少早熟收敛现象的发生[13-15]。利用二者的优势互补性，本文提出一种混合粒子群（Hybrid Particle Swarm Opti-mization，HPSO）算法。

粒子位置和速度的交叉操作过程为：

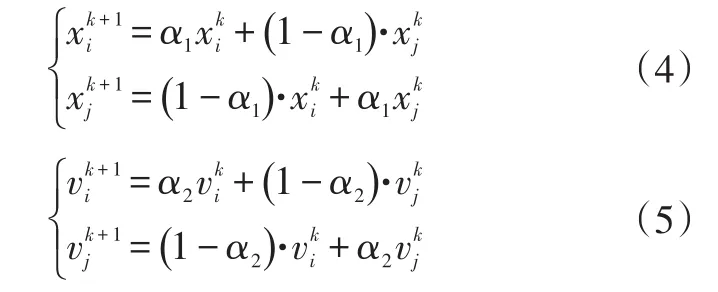
式中，α1、α2为[0,1]范围内的随机数；粒子分别为粒子进行交叉操作后的子代粒子。

解的质量依赖于变异率的选择，本文采用随机扰动的方法对当前个体极值pbest进行高斯变异操作。对于每个粒子的当前最优极值，按照一定的概率pm实行变异，β服从gauss(0,1)分布，公式如下：

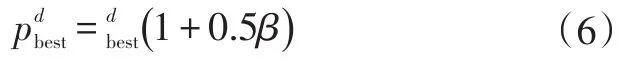
3.3 基于HPSO-BP神经网络的锂电池SOC预测模型

鉴于HPSO算法具有收敛速度快、不易陷入局部极小的优点，可用于BP神经网络初始权值和阈值的优化，本文基于HPSO-BP神经网络算法进行锂离子电池SOC的预测。HPSO-BP神经网络联合算法流程为（见图2）：

a.根据输入、输出样本集设计BP神经网络输入层、隐含层和输出层的神经元个数，确定网络拓扑结构；

b.粒子群初始化，粒子群的大小取BP神经网络中所有权值w和阈值b的个数和，由于BP神经网络结构设置为4-12-1，得到粒子维数d=4×12+12+12×1+1=73，学习因子c1、c2均设置为2，设定最大迭代次数itermax=300，误差精度设定为0.001；

c.适应度计算，根据适应度函数计算各粒子的适应度，确定每个粒子的个体最优极值pbest和群体最优极值gbest；

d.判断算法是否达到终止条件（最大迭代次数或者误差精度），如若满足，则迭代结束，将最优群体极值定为BP神经网络最优初始权值阈值，进行网络训练与测试，否则进入下一步迭代；

e.更新粒子群，按照式（1）和式（2）更新粒子速度和位置，并计算各粒子的适应度，然后更新粒子的个体极值pbest和群体极值gbest；

f.个体、群体最优粒子的交叉、变异操作，根据式（4）和式（5）完成粒子群位置和速度的交叉操作，然后根据式（6）完成变异操作；

g.采用轮盘赌法进行最优个体的保留与剔除。

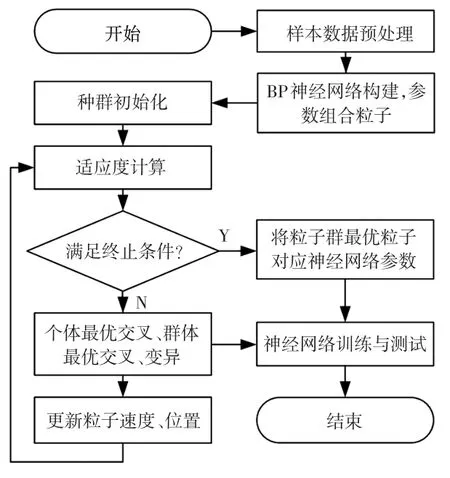
图2 HPSO-BP神经网络联合算法流程

4 仿真与结果分析

4.1 样本数据选取

利用Neware公司的充放电测试仪记录磷酸铁锂电池（4.2 V，1.75 A·h）的工作电压、电流、温度、内阻和容量，从中提取580组数据作为样本数据，部分样本数据如表1所示。

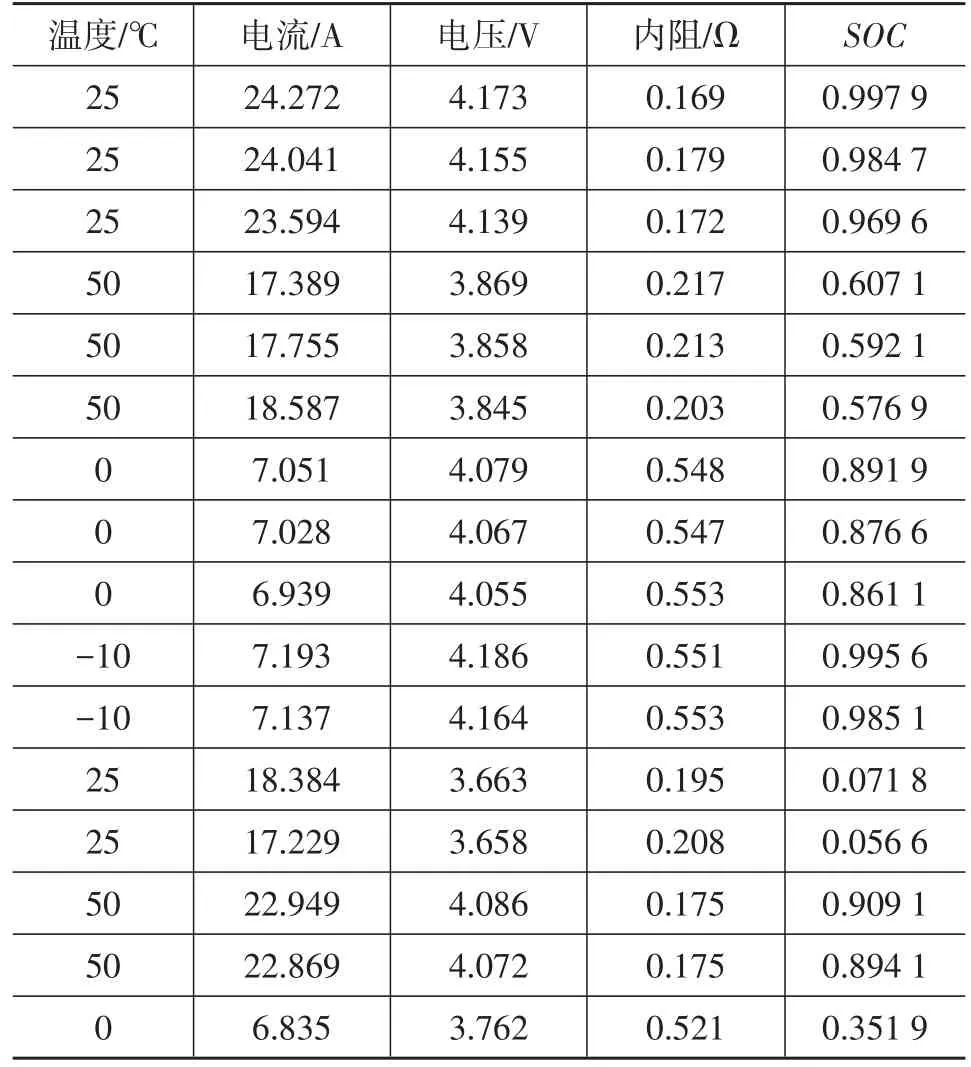
表1 部分样本数据

由于本文BP神经网络中的激活函数为logsig函数，故将上述样本数据进行归一化处理：

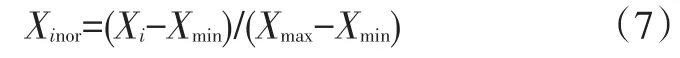
式中，Xi、Xinor分别为样本值及其归一化值；Xmin、Xmax分别为样本数据中的最小值和最大值。

4.2 仿真与结果分析

为了验证HPSO-BP神经网络算法预测锂电池SOC的准确性和快速性，以BP神经网络均方根误差（Root Mean Square Error，RMSE）作为适应度评估函数：

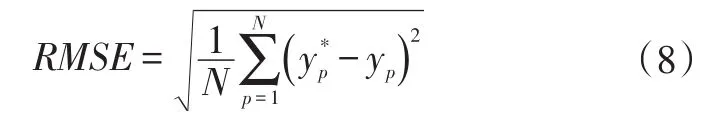
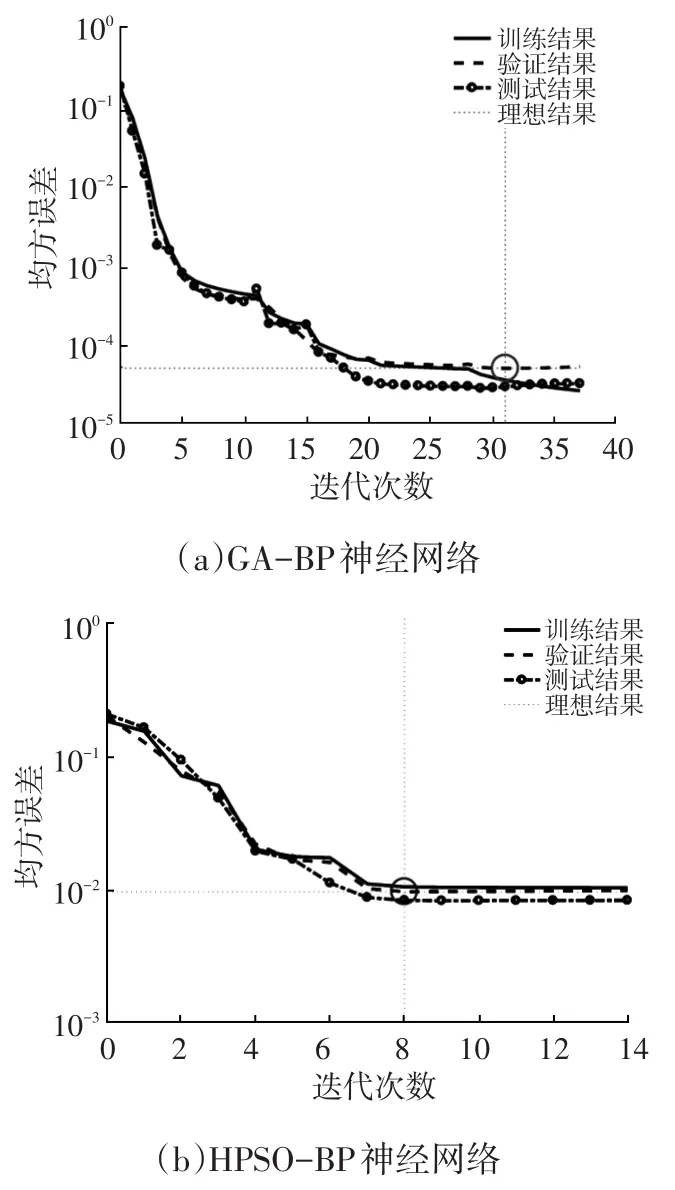
图3 仿真误差迭代曲线

从图3a中可以看出，GA-BP神经网络在第32次迭代达到网络设定精度，训练和验证迭代速度大致相同，测试速度相对较慢；图3b中，HPSO-BP神经网络在第8次迭代就达到了网络所设置的精度，并且迭代速度基本保持同步。通过对比可知，HPSO-BP神经网络表现出了更快的收敛速度。

图4所示为网络估算锂电池SOC及其期望值。从图4中可以看出，两种网络算法都取得了不错的预测效果，为了凸显HPSO-BP神经网络算法预测锂电池SOC的准确性，绘制两种网络算法的误差精度曲线如图5所示。

从图5中可以明显看出：GA-BP神经网络算法的输出结果误差大部分保持在4%以内，最大误差接近6%，达到了目前行业要求的低于8%的误差精度；HPSO-BP神经网络算法的输出结果误差基本保持在2%以内，最大为3%，表现出了更高的估算精度。

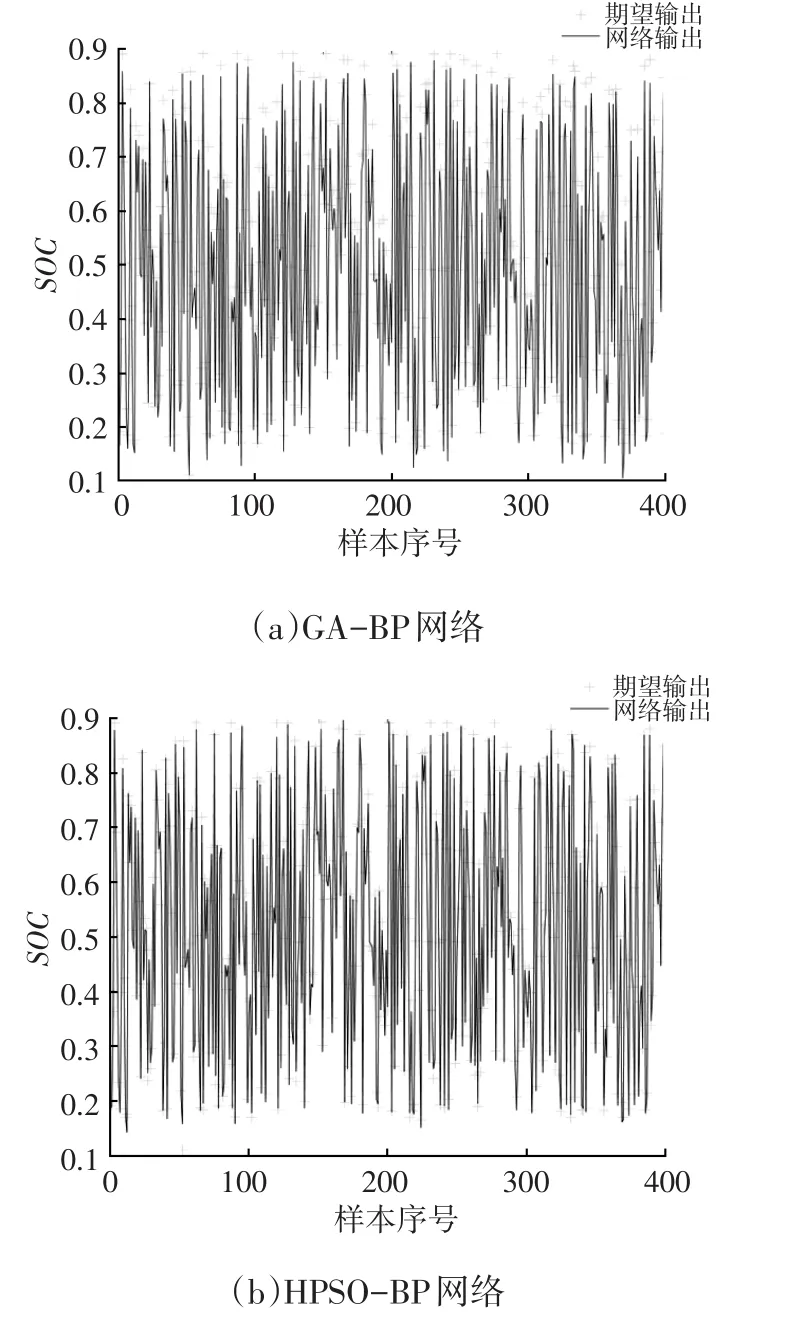
图4 网络输出与期望输出对比

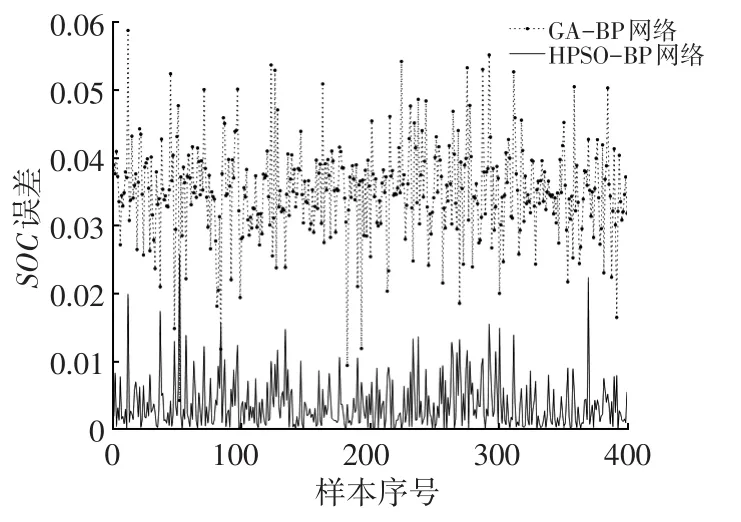
图5 网络估算SOC误差曲线

5 结束语

本文通过运用改进后的粒子群算法优化BP神经网络初始权值阈值敏感、容易陷入局部极小值等缺点，建立锂离子电池荷电状态估算模型，仿真结果表明，该联合算法与传统BP神经网络相比更具快速收敛性、准确性和稳定性。