基于道路工况预测的混合动力汽车自适应等效燃油消耗最小策略＊

邓涛 罗远平 程栋 罗俊林

（重庆交通大学，重庆 400074）

主题词：混合动力汽车 能量管理 车速预测 坡度预测 仿真

1 前言

混合动力汽车结合了纯电动汽车的节能优势和传统汽车的动力性，其动力系统一般有2种或2种以上的动力源，这就需要依靠能量管理策略对各动力源的工作状态进行合理的控制。相较于其他能量管理策略，实时优化策略可通过求解局部最优解获得接近于全局最优的结果，且具有实时在线优化的能力。常见的实时优化能量管理策略有动态规划（Dynamic Programming，DP）[1]、极小值原理（Pontryagin's Minimum Principle，PMP）[2]、模型预测控制（Model Predict Control，MPC）[3]以及等效燃油消耗最小策略（Equivalent Consumption Minimization Strategy，ECMS）[4-6]等。其中，ECMS计算速度快，容易实时控制，最有希望应用于实车，但其需要知晓整个循环工况来求解全局燃油经济性最佳的等效因子，因此，工况的确定是ECMS的重要前提。另外，传统的ECMS在整个行驶工况中只利用单一的等效因子，会导致SOC偏离较大。所以，ECMS在进行计算时需要根据预测工况或SOC反馈实时调整等效因子，即形成基于工况预测调节的自适应等效燃油消耗最小策略（Adaptive Equivalent Consumption Minimization Strategy，A-ECMS）[7]和基于SOC反馈的自适应等效燃油消耗最小策略[8]。其中，基于SOC反馈的A-ECMS在整个行驶工况中SOC波动比较频繁，会降低电池的使用寿命。

工况预测主要包括车速预测和坡度预测两部分。对于车速预测，神经网络[9]、马尔科夫链[10]和灰色预测[11]等预测方法应用较为广泛。神经网络需要存储大量的历史数据进行离线训练，马尔科夫链也需要大量的历史数据作为样本来确定转移概率矩阵，而灰色预测建模是基于少量数据，根据新陈代谢原理建立的等维信息模型，使信息保持“新鲜”性的同时不增加计算量，特别适合在实时控制系统中应用[12]。对于坡度预测，可以利用智能交通系统（Intelligent Transport System，ITS）（包括GPS/GIS）对坡道进行预测，但需要较高品质的GPS信号作为保障，低成本的GPS模块很难达到很好的计算效果[13]，此外，带遗忘因子的最小二乘法[14]或卡尔曼滤波[15]等方法也常用于在线估算道路坡度，卡尔曼滤波在计算的精确性和算法的稳定性方面都优于带遗忘因子的最小二乘法。

因此，本文采用预测工况实时调整等效因子，建立基于道路工况预测的A-ECMS。对灰色预测算法中的权系数进行迭代寻优，提高了未来车速预测精度；研究了道路坡度的线性关系，提出对卡尔曼滤波估计出的道路坡度进行线性拟合，并以拟合的线性函数的曲率变化来预测道路坡度。最后根据预测的未来短期道路工况调整合适的等效因子，达到优化SOC轨迹、优化需求转矩分配以及提高燃油经济性的目的。

2 道路工况预测

2.1 基于改进型灰色预测的车速预测

以某款并联式AMT混合动力汽车作为研究对象，结构如图1所示，主要部件参数如表1所示。

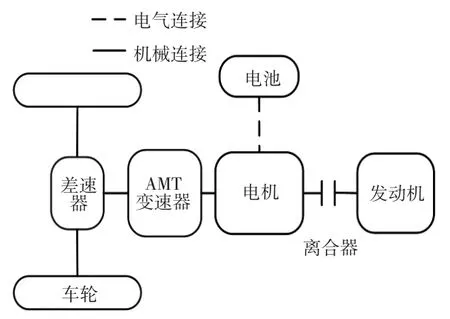
图1 并联式HEV动力系统结构

采用灰色预测算法进行车速预测时，首先要确定用于计算的原始数据数列。对于车速预测来说，汽车行驶速度为随时间变化的一系列参数，杨盼盼[11]通过分析得到利用过去12 s的车速信息预测未来6 s的车速信息最为合理的结论，但本文在算法上与其不同，根据实际需要，决定以过去10 s车速信息预测未来10 s车速。因而基于灰色预测的车速预测的原始数据序列X(0)为汽车前10 s的速度数据序列。

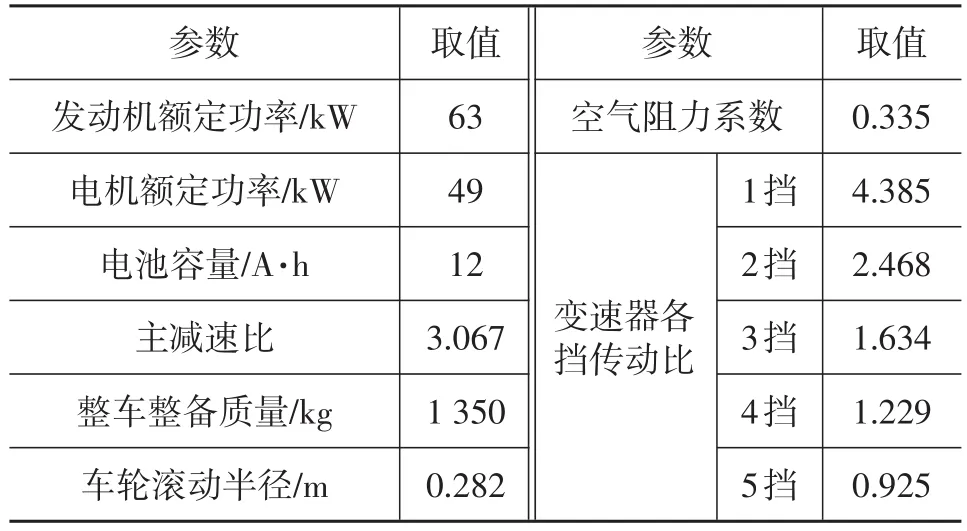
表1 整车参数

将原始数据依次累加，生成具有较好规律的1-AGO累加序列。再将1-AGO序列相邻数据分别乘以权系数μ生成紧邻序列并进行相应参数求解，然后对所得数据序列累减得到原始序列的预测值，最后再对未来值进行预测[16-18]。在分析灰色预测算法计算过程时发现，为简化计算量，一般取μ=0.5，但这会影响预测精度。因此选用迭代计算，以数据的平均相对误差为判断依据寻求最优权系数，其具体过程见文献[19]。

经过计算，可以得到原始序列的拟合方程为：

式中，a为发展系数；b为内生控制系数；^(0)为原始数据拟合序列；x(0)(1)为原始数据序列的第1个数据。

经大量仿真分析发现，发展系数a→0时，灰色预测模型的精度相对较高，也表示与前一段时间车速相关性较强。于是在仿真条件下设定当|a|＜0.1时，车速与上一秒车速相等，即汽车匀速行驶。

2.2 道路坡度预测

2.2.1 基于卡尔曼滤波器的坡度估计

对于本文，汽车行驶时的各项参数均被离散化，而离散卡尔曼滤波则以递归的方法解决离散数据的线性滤波问题，可对离散时间控制的过程进行估算。因此，应用离散卡尔曼滤波器对实时变化的道路坡度进行估算。

由汽车的驱动力平衡方程可得：

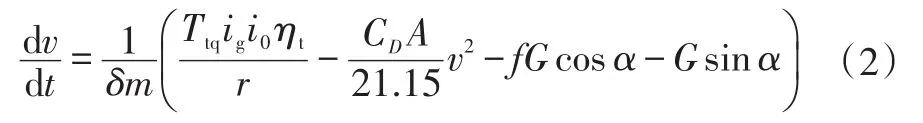
式中，v为车速；δ为旋转质量系数；m为质量；Ttq为发动机转矩；ig为变速器各挡传动比；i0为主减速器传动比；ηt为传动系效率；r为车轮滚动半径；CD为空气阻力系数；A为迎风面积；f为滚动阻力系数；G为重力系数；α为路面坡度。

因此，k时刻的速度可以用(k-1)时刻的速度及其加速度进行估计：

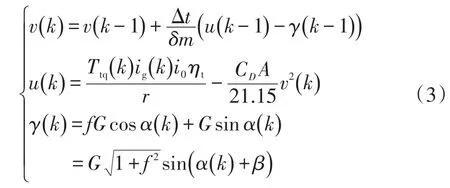
式中，Δt为采样时间间隔；β=arctanf为等效道路坡度。

将u(k)作为输入量，车速作为观测量，状态变量为：

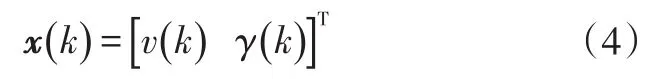
于是，汽车纵向动力学方程的卡尔曼滤波形式为：

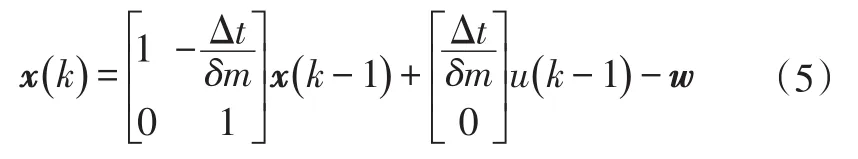
系统的观测方程为：

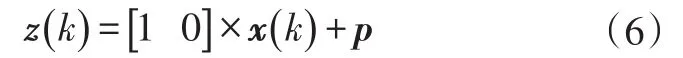
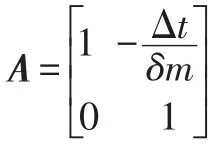
系统开始计算时，给定车速、坡度的初始值以及过程噪声协方差矩阵Q和观测噪声协方差矩阵R，卡尔曼滤波器就可以根据图2进行计算（其中-表示先验，^表示估计），不断估计实时道路坡度。

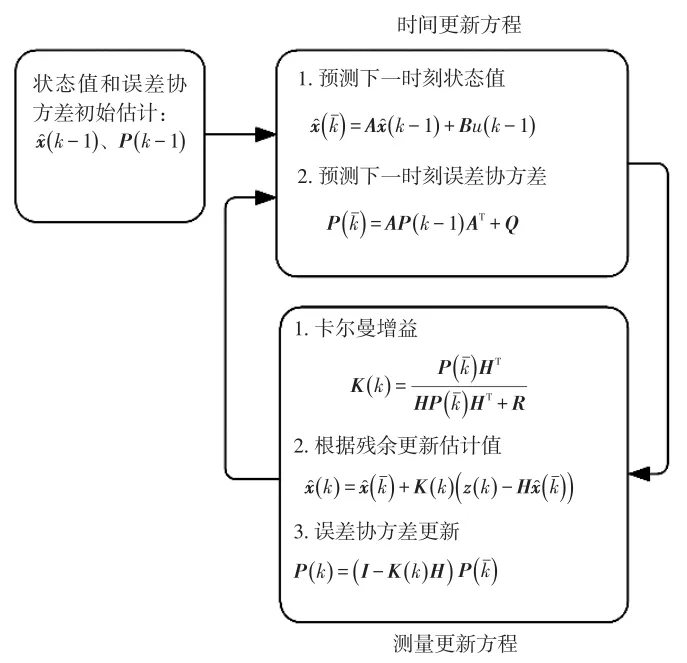
图2 卡尔曼滤波算法流程

2.2.2 道路坡度线性拟合

道路本身具有线性特性，某一时间段内的道路可以以线性函数y=f(x)表达。因此，在已识别出当前道路坡度的情况下，可以通过拟合道路坡度随时间的函数来预测道路坡度。如图3所示，M、P为某次道路坡度拟合函数上的2个点，l、t分别为函数曲线经过M点、P点的切线，φ、y分别为曲线在M点、P点的斜率，RM、RP分别为曲线在M点、P点的曲率半径，N、Q分别为坡度变化前、后路段上的点。可以看出：N点之前与Q点之后的道路坡度没有发生变化，其曲率半径为无穷大，所以将此路段看作直线并用一次函数拟合；过渡段M、P的曲率半径先减小后增大，可将NQ段看作开口向上的抛物线，即用二次函数对其进行拟合。于是，将道路坡度的预测转为对路面曲率半径变化的计算问题，即当道路坡度将要产生变化时，路面拟合函数的曲率半径会明显降低。

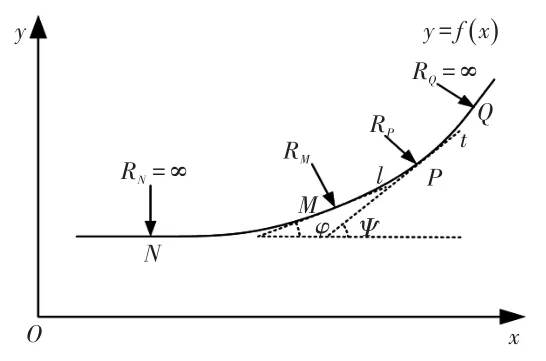
图3 道路坡度函数曲率变化示意

函数上某点的曲率和曲率半径为：

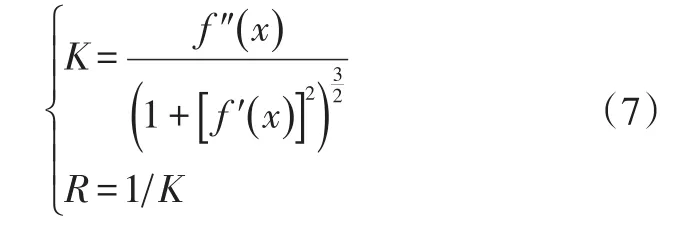
当R=∞时，曲线为直线；R＞0时，曲线为凸曲线；R＜0时，曲线为凹曲线。

3 基于道路工况预测的A-ECMS

混合动力汽车能量管理策略的实质是根据汽车实时运行状态将转矩合理分配给发动机和电机，在满足汽车动力性以及维持SOC轨迹的前提下获得最佳燃油经济性。本文通过未来短期道路工况预测，对工况进行预判并以此实时调整等效因子，以提高燃油经济性。

未来短期各时刻的变速器输入轴转矩Tin(i)和转速nin(i)分别为：

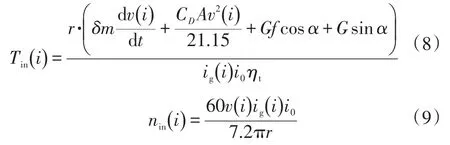
各时刻的需求转矩确认后，等步长地将等效因子λ取值范围[λmin,λmax]划分为S步，同样地将电机的转矩取值范围[Tm,min(nm),Tm,max(nm)]划分成j步，计算每一步长发动机分配到的转矩：

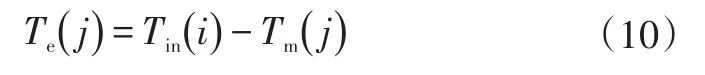
式中，Te为发动机转矩；Tm为电机转矩。

每步长对应的电机输入功率为：

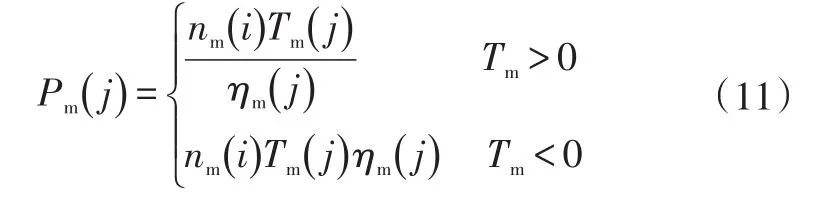
式中，ηm为电机效率；nm为电机转速。

每步长对应的电池电流为：

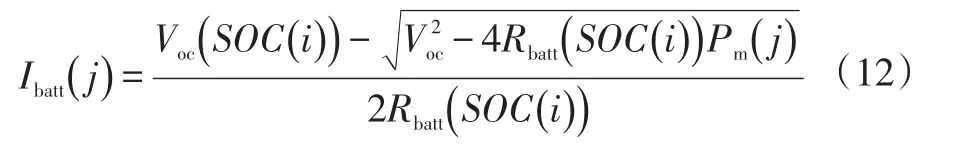
式中，Rbatt为内阻；Voc为开路电压。

每步长对应的电池功率为：

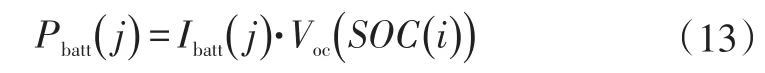
每步长对应的发动机油耗e(j)由发动机转矩Te(j)和转速ne(i)共同决定，可由发动机MAP图通过插值求得：

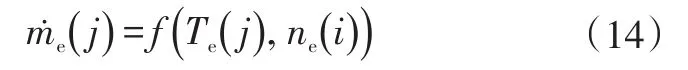
每一步长对应的等效油耗为：

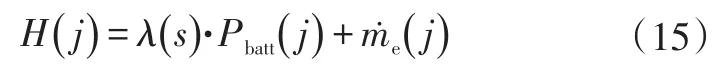
求得某一等效因子下每一时刻最小等效油耗为：

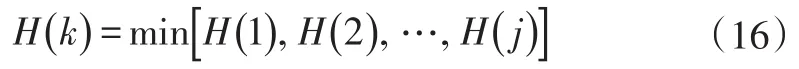
故该等效因子下最小等效油耗对应的SOC变化量ΔSOC为：

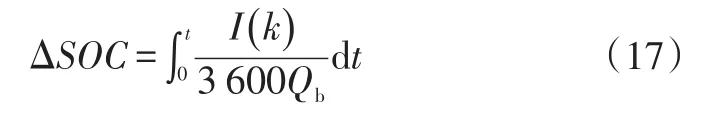
式中，Qb为蓄电池最大容量。

再将每步长等效因子对应的最小等效油耗进行排序：Hmin,Hm,Hn,…,Hmax。

接下来判断Hmin对应的ΔSOC是否在允许的控制范围内，如果超过控制范围，重新选择最接近Hmin的Hm判断对应的ΔSOC，以此类推，直到ΔSOC的范围在允许的控制范围内为止，此时的等效因子值即为所求的λ*。

最后将所求最优等效因子λ*作用于当前时刻，并以等效油耗最小为目标重新进行最优转矩分配，最终得到最佳的分配转矩u*。此时所得结果即为A-ECMS在SOC、等效因子以及转矩分配都达到最优时的控制参数，哈密顿函数H(SOC*,λ*,u*,t)此时达到最优值。

4 仿真分析

为验证改进后灰色预测GM(1,1)模型预测的准确性，在VAIL2NREL工况下进行仿真验证，结果如图4所示。经过仿真计算，该工况下预测未来10 s车速的平均绝对误差为1.158 5 km/h，在整个工况下，该精度可以接受，说明该改进型灰色预测应用于速度预测是可行的。

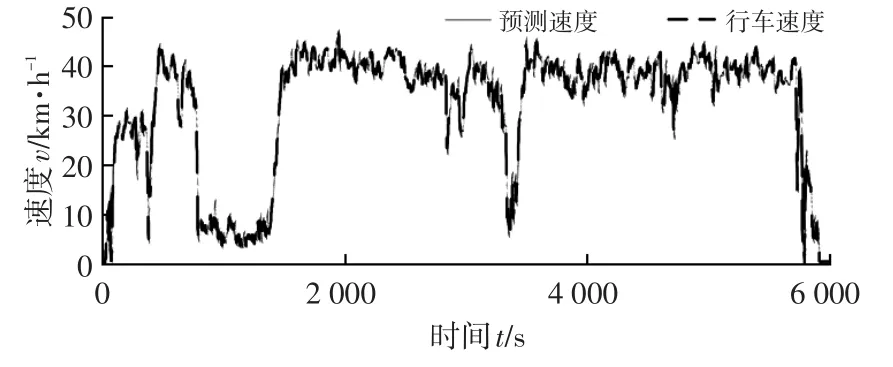
图4 VAIL2NREL工况下预测速度与实际速度的对比

图5所示为某道路模型的预测结果。可以看出，在整个工况条件下短期预测的结果与卡尔曼滤波估算结果跟随性较好。经计算，预测的平均误差为0.056 7°，证明了本文所用坡度预测方法的可行性。

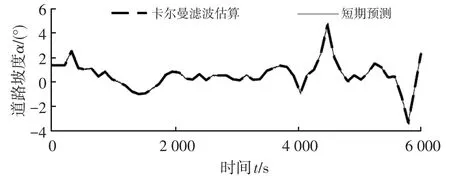
图5 道路模型坡度预测结果

在VAIL2NREL工况下进行性能仿真分析，结果如图6所示。SOC的波动范围为-0.025～0.065，终值与初始值相差0.062，轨迹整体保持稳定；电机充电时转矩较大，而驱动时转矩不高，发动机整体工作转矩较大。

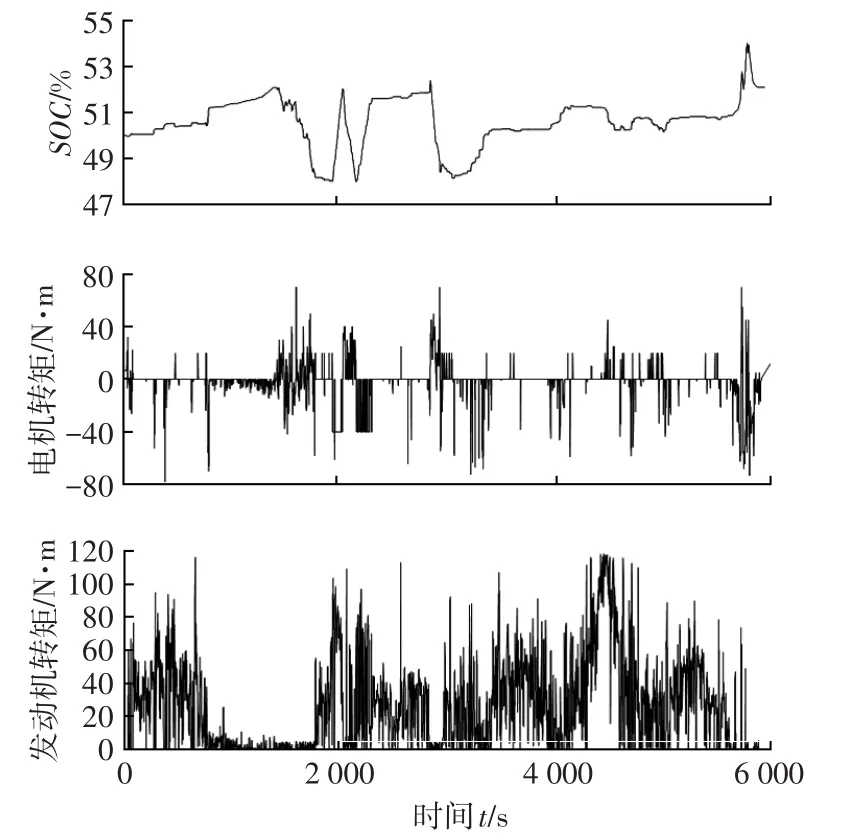
图6 VAIL2NREL工况下仿真结果

图7所示为两种A-ECMS在VAIL2NREL工况下SOC仿真结果以及对应时间点的道路坡度情况。可以明显看出，基于SOC反馈的A-EMCS在整个工况下SOC的波动频率比较明显，而基于道路工况预测的A-ECMS在整个工况下SOC轨迹保持依然较好，同时没有频繁波动，更没有明显的通过改变等效因子调整SOC轨迹的现象，因为此控制策略的优化目标是所预测未来短期道路工况下SOC、等效因子、燃油消耗量以及需求转矩分配共同决定的最优哈密顿函数。

图7 VAIL2NREL工况下两种A-ECMS SOC控制结果对比

图8所示为两种A-ECMS在VAIL2NREL工况下电机转矩及对应转速点的电机效率分布情况，可以明显看出，基于SOC反馈的A-ECMS电机运行在高转矩的点数更多，而基于道路工况预测的A-ECMS转矩相对较低，但电机效率分布相差不大，说明控制策略在降低电机工作转矩的情况下，并没有降低效率。

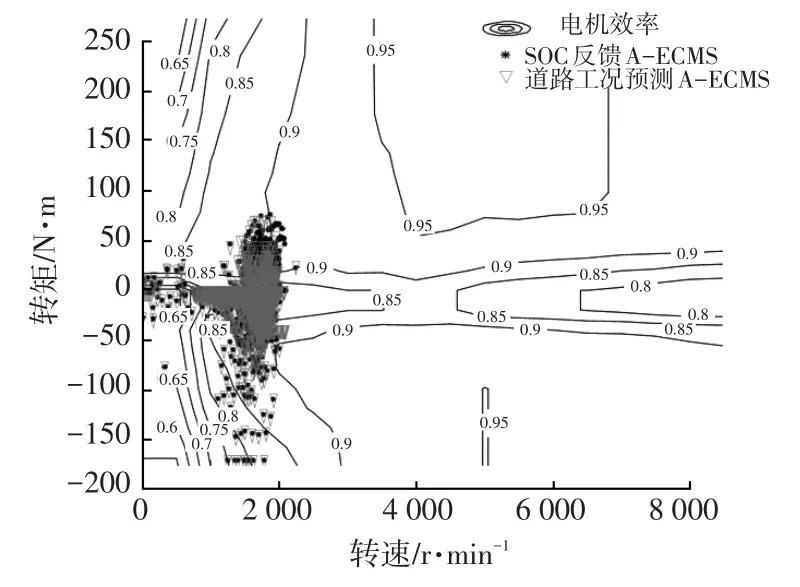
图8 VAIL2NREL工况下两种A-ECMS电机转矩分布

图9所示为两种A-ECMS在VAIL2NREL工况下发动机转矩及对应转速点的燃油消耗率分布情况，可以看出相比于基于SOC反馈的A-ECMS，基于道路工况预测的A-ECMS发动机工作点更多集中在低燃油消耗率的区域，油耗降低效果明显。

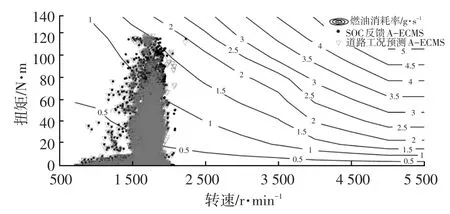
图9 VAIL2NREL工况下两种A-ECMS发动机扭矩分布

基于SOC反馈的A-ECMS的百公里燃油消耗量为4.294 L，基于道路工况预测的A-ECMS的百公里燃油消耗量为4.013 L，后者较前者相对降低了6.54%。

5 硬件在环仿真验证

为验证控制策略的实时性和稳定性，搭建硬件在环（Hardware In Loop，HIL）仿真验证平台，如图10所示。在Simulink中建立混合动力汽车整车模型，提取出控制策略，添加输入、输出驱动模块以及CAN通信配置模块，接收整车模型各部件的控制信号，同时输出车速信号、油门踏板信号和制动踏板信号等。将整车模型进行编译生成C代码，自动下载至AutoBox中。

图10 硬件在环实物图

采用Freescale公司的MPC5634M作为主控芯片，dSPACE标准组件系统采用DS1005PPC处理器板，其使用的是Freescale的POWER体系的PC750GX处理器，处理频速933 MHz。CAN通信模块总线驱动器采用博世公司CF160CAN驱动芯片，通信格式为标准帧格式，波特率为250 kb/s，报文协议为J1939协议。整车控制器以10 ms的中断周期实时进行AD信号采集、控制策略的运行以及CAN信号发送。

采用与离线仿真相同的VAIL2NREL工况，如图11所示，控制器分配转矩与目标需求转矩趋于一致，说明提出的控制策略具有较好的实时性和稳定性。但从局部放大图来看，分配转矩曲线滞后约35 ms，这是整车控制器运行控制策略消耗时间造成的，而人体对外界刺激的感知时间为100 ms左右，因而驾驶员不会有“加速疲软”的感觉。另外，由于“时滞”效应，HIL仿真百公里燃油消耗量为4.108 L，相比于离线仿真增加了2.37%。

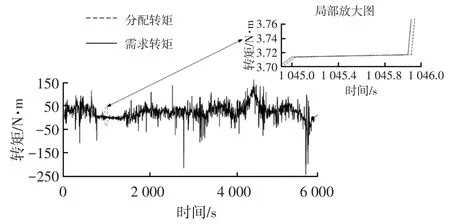
图11 需求转矩与分配转矩对比

SOC控制结果和功率分配的仿真结果如图12、图13所示，显然，HIL仿真与离线仿真的结果趋于一致，也验证了该策略的有效性。

6 结束语

为提高传统A-ECMS在坡度工况下的适应性，在车速预测的同时对道路坡度进行预测。根据道路坡度的线性特性，提出了基于卡尔曼滤波估算坡度的线性拟合预测方法，并将预测的车速与道路坡度用于实时调整等效因子，建立基于道路工况预测的A-ECMS策略。结果表明，该坡度预测方法结果较为准确，且以此为基础的A-ECMS相比于基于SOC反馈的A-ECMS，SOC轨迹的波动明显减少，同时燃油经济性也提高了6.54%。通过硬件在环仿真验证了该控制策略的实时性和稳定性，说明该控制策略应用于实车是可行的。

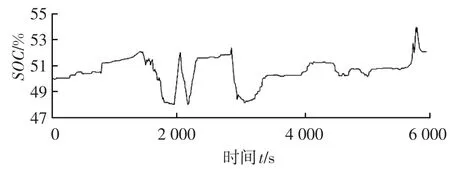
图12 硬件在环SOC仿真结果

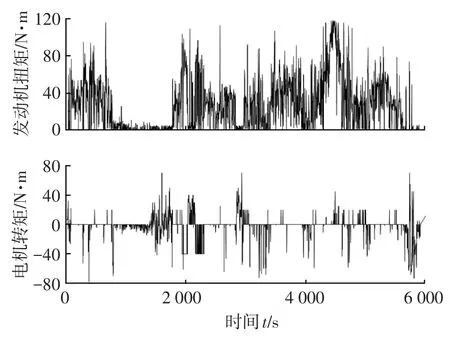
图13 硬件在环仿真转矩分配