T型三通管冷热流体掺混数值模拟

邹智鑫 王合旭 蒋彦龙 李泽伟

摘要：针对T型三通管冷热流体掺混现象经常引发管道热疲劳甚至部件失效的问题，基于FLUENT混合雷诺平均N-S方程（Reynolds averaged N-S equations，RANS）和大涡模拟（large eddy simulation， LES）方法，对其管内冷热流体掺混问题进行仿真模拟。对划分的LES和RANS计算域分别采用壁面模拟LES（wall-modeled LES， WMLES）和k-ω SST模型进行计算，并将数值模拟结果与实验数据进行对比。分析功率谱密度（power spectral density， PSD），预测管内冷热流体掺混过程的热疲劳敏感位置，结果表明：数值模拟预测结果与实验数据吻合度较高，热疲劳敏感位置也与实际情况相符合。混合RANS-LES方法适用于T型三通管冷热流体掺混问题研究。

关键词：T型三通管;冷热流体掺混;功率谱密度;热疲劳

中图分类号：TL331;TK172.4

文献标志码：B

文章编号：1006-0871（2019）01-0046-07

0 引 言

T型三通管广泛应用于各种装置的管道系统中。在核电站热力管线的三通管中，其主路和支路流体温度不同，在三通管内进行冷热流体掺混，尤其是在三通管内主路下游区域温度波动较大，管壁受到交变温度载荷进而造成管道热疲劳问题。因此，研究三通管内冷热流体掺混过程意义重大。本文提出一种基于FLUENT的数值模拟研究方法，进行相应的热疲劳分析。

大涡模拟（large eddy simulation， LES）是近年發展起来的研究湍流的重要数值模拟方法，该方法适用于三通管内流体掺混的模拟。一直以来，国内外学者对三通管均有一定的研究，包括实验研究和数值模拟研究。TAKAHASHI等[1]通过实验研究两股流体混合后温度波动的特征，结果表明主路与支路流体的速度比和直径比对流动模式有重要影响。SHIGETA等[2]对混合三通管进行可视化实验，在一定范围的速度比内观察到周期性的涡流，认为涡流与温度波动密切相关。KAMIDE等[3]进行实验与数值模拟混合研究，对比不同动量比情况下冷热流体混合的三通管，通过可移动的热电偶树和粒子图像测速仪测量详细的温度和速度场，认为三通管中的流动模式可分为3类：壁面射流、偏转射流和冲击射流。

CHAPULIOT等[4]通过数值模拟计算分析三通管管件裂缝的形成和生长过程，在LES的基础上使用非常大涡模拟（very large eddy simulation， VLES）进行计算，阐明湍流热负荷对结构的影响。AYHAN等[5]使用雷诺平均N-S方程（Reynolds averaged N-S equations，RANS）k-ε模型和LES模型研究混合区域的速度和温度波动频率，对比分析结果发现，LES在粗细网格中得出的结论均与实验结果一致。HOWARD等[6]进行混合三通管的额定数值模拟，比较RANS与LES模型的计算结果，认为在开发出更可靠的模型前，最好使用LES方法研究T型三通管热掺混问题。FERRARA等[7]使用LES模型研究带有液体钠的T型三通管中的热波纹现象，发现LES在粗网格情况下的结果不完全可靠，建议加强网格质量并为特定的问题选择特定的子网格模型。SELVAM等[8-10]考虑子网格模型，在LES中流动产生的大涡被直接解析，较小的涡使用亚格子尺度（sub-grid scale， SGS）模型进行建模，使用壁面自适应局部涡黏模型对涡流黏度进行建模，分析不同温度差流体进行热混合的情况，模拟结果表明LES的平均温度预测与实验数据表现出良好的一致性，而温度波动均方根（root meam square， RMS）在温差较高时出现某些位置值偏高或偏低现象，温差较低的数据结果也与实验一致。运用同种模型方法，GAUDER等[11]研究不同的入口条件对混合三通管下游流体流动特性的影响。

在最近几年，部分研究采用混合RANS-LES方法进行三通管热混合的模拟。此方法可以很好地解决LES需要大量时间的弊端，也能够获得RANS不能得到的诸如大尺度涡结构和性质等动态信息。ZENG等[12]采用混合RANS-LES方法的计算结果，与只用RANS模型相比更接近实验数据，且相对于LES方法可节省大量的计算工作量。KRUMBEIN等[13]和CHANG等[14]使用基于VLES的混合RANS-LES方法进行研究，获得的结果与实验数据非常吻合。GRITSKEVICH等[15]将基于剪切应力传输模型的改进延迟离散涡模拟SST-IDDES方法与近壁处理NWT相结合，对具有壁函数的混合RANS-LES方法进行评估，认为此方法对于较粗网格也能得出较好的结果。

这些研究工作表明，LES模型比其他模型更适用于T型混流三通管的研究，但是LES模型不可避免地存在计算量较大、计算周期过长的缺点，于是混合RANS-LES应运而生。本文采用嵌入式LES（embedded LES， ELES）模型进行数值模拟，并将结果与KAMIDE等[3]的实验结果进行对比。

1 模型介绍

1.1 数学模型

1.1.1 控制方程

1.1.2 SGS模型

采用壁面模拟LES（wall-modelled LES， WMLES）模型对壁面进行建模处理，不同尺度的涡通过SGS模型建立联系。基于Boussinesq假设，残余应力张量

1.2 物理模型与边界条件

为便于对比，采用KAMIDE等[3]异径三通管实验模型尺寸（见图1），其主路直径为Dm=150 mm，主路上游段长度约为4.33Dm，下游段长度约为3Dm，支路直径为Db=50 mm，长度为2Dm，热流体从左边向右边流动。

冷热流体的进口边界条件为充分发展的湍流边界，由RANS模型进行前处理获得速度和湍流等参数，温差为15 ℃;出口边界条件设置为压力出口。管壁边界均设置为绝热和无滑移条件。选取图1中Z=-1.0Dm和Y=-2.0Db这2个面设置为RANS-LES-interface，阴影区域为LES计算域，其余区域为RANS计算域。

1.3 网格划分和计算方法

将模型分为3个区域划分网格，整体网格见图2。网格较为稀疏的主路和支路上游（图2中左侧和下侧）为RANS计算域网格，LES计算域网格为加密网格。局部加密网格见图3。由于网格均为结构网格，所以块与块之间的网格结合面不需要进行合并节点设置，可直接在FLUENT中设置为interface。

RANS计算域采用k-ω SST模型，LES计算域采用WMLES模型。在FLUENT中采用SIMPLE算法，动量方程选用二阶迎风格式，瞬态项格式設置为二阶隐式。设置合适的收敛因子，取时间步长为0.005（即CFL约为5）。

2 计算结果与分析

2.1 实验验证

KAMIDE等[3]的实验数据包括壁面射流、偏转射流和冲击射流等3种混合工况，此处将壁面射流的数值结果与其实验结果进行对比，验证数值方法的准确性。将温度及其RMS值进行无量纲化，即

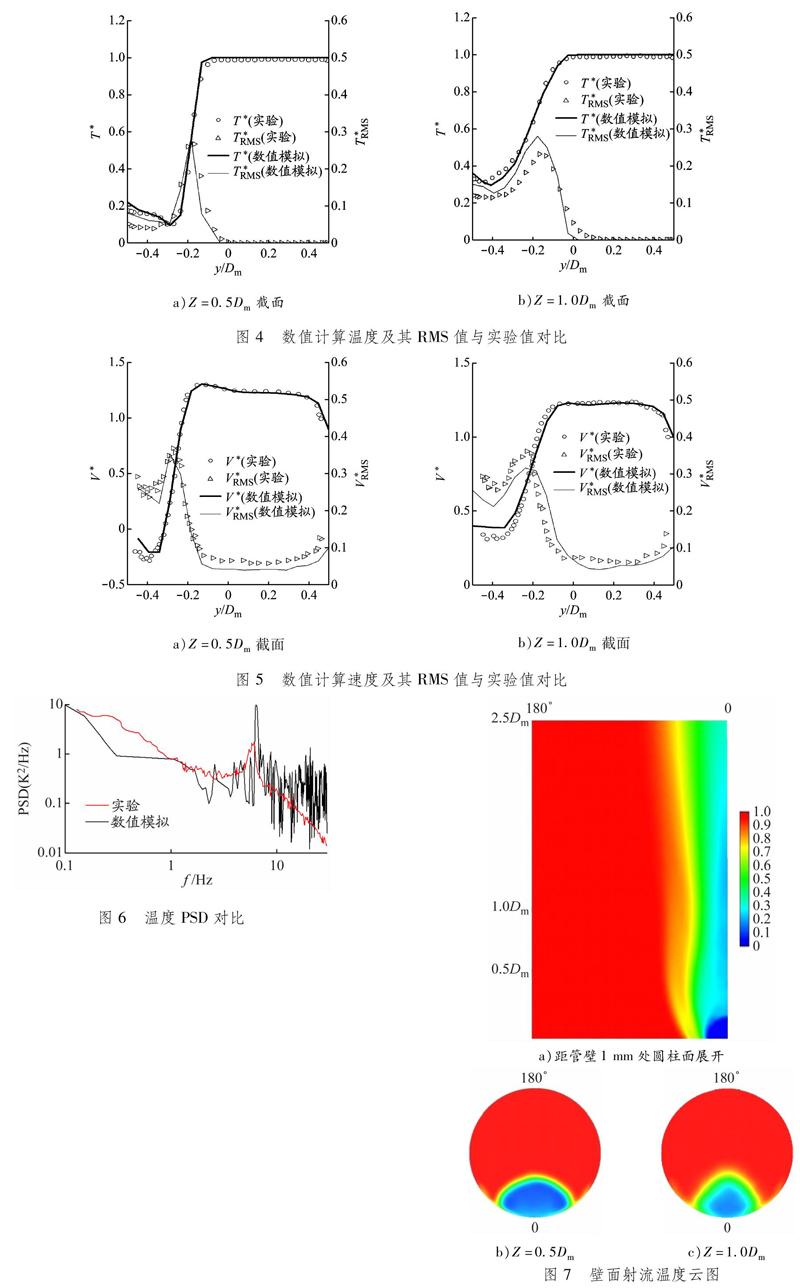
选取Z=0.5Dm和Z=1.0Dm截面，得到2个平面上的温度值及其温度RMS值的无量纲数，与实验结果进行对比，见图4。由此可知：数值计算结果与实验结果误差在允许范围内;在Z=0.5Dm截面上温度变化最剧烈的点大约位于y=-0.2Dm处，在Z=1.0Dm截面上温度变化最剧烈的点大约在y=-0.15Dm处，说明支路流体还有向主路底部冲击的速度，这与实际流动相符。

将速度和速度波动无量纲化，即

同样选取Z=0.5Dm和Z=1.0Dm截面，得到2个平面上的速度及其RMS值的无量纲数，与实验结果对比见图5。V*与实验数据保持较高的吻合度，V*RMS与实验数据的误差在允许范围内。

在距主路管壁10 mm、交平面Z=1.0Dm且θ=30°处取一点，根据采集到的温度数据进行功率谱密度（power spectral density， PSD）分析，并与实验数据进行对比，见图6。由此可以看出，数值模拟结果与实验数据较一致，特征频率均在6 Hz左右。

通过以上对比发现，数值模拟与实验数据均具有较高的吻合度，尤其是温度和速度误差都非常

小，温度和速度波动值有一定误差，但在误差允许范围内，说明本文数值模拟方法可以有效评估三通管冷热混流现象。

2.2 数值模拟结果分析

2.2.1 温度云图与流线图

设定壁面射流主路和支路进口流速分别为1.46和1.0 m/s，冲击射流主路和支路进口流速分别为0.23和1.0 m/s。对壁面射流和冲击射流的云图及流线图进行分析，见图7～12。

温度云图与KAMIDE等[3]实验数据的吻合度较高。冷热流体交界处出现高强度的温度波动，壁面射流的高波动区域大致为圆弧状，并随着流体向下游流动，有变小的趋势;圆弧中间的低波动区域颜色逐渐加深，即波动逐渐变大，说明冷热流体掺混越来越均匀。冲击射流主路流速较低，导致支路冲击到壁面，圆弧状的高波动区域向底部壁面移动。通过流线图可以清晰地看到冷热流体的交界面，且下游区域均出现放射状的流线，可见在此处形成漩涡，见图13。

2.2.2 疲劳分析

PSD能够直接反映温度波动与频率变化的关系，是热疲劳分析中最重要的参数之一。[16]本文用PSD对主路底部管壁疲劳情况进行预测分析。沿下游方向取6个点，分别取Z为0.3Dm、0.5Dm、0.7Dm、1.0Dm、1.5Dm和2.0Dm，即图1中A～F点，研究工况为冲击射流。各位置瞬时温度和速度PSD曲线分别见图14和15。

由图14可以看出：C点的温度PSD曲线处于最高位置，B点与C点差距不大，其余位置点PSD值均明显小于C点;温度PSD从A点最小开始，上升到C点位置后又逐渐下降，这与混合流动密切相关，表明C点位置附近是混合交界线处，温度波动最大，而后混合越来越均匀，波动减小。图15也体现出类似的规律，说明C点可能处于热疲劳点，另外B点、D点也有可能是热疲劳点。

3 结束语

围绕T型三通管内的冷热流体掺混流动，应用基于FLUENT的混合RANS-LES方法，研究冷热流体交汇处的温度波动问题。数值模拟结果与实验数据吻合较好。分析壁面射流和冲击射流温度分布及其波动强度，验证混合RANS-LES方法在T型三通管内冷热掺混流体问题研究中具有可靠性。对比观察不同位置点的温度和速度PSD，结果表明在冲击射流工况下，位于下游约Z=0.7Dm点处PSD值较高，故考虑该处为相关工况下结构热疲劳的敏感点。由此方法得出的温度分布以及温度波动数值能够保证热应力、热疲劳分析研究的准确性。

参考文献：

[1] TAKAHASHI S， SHIINA K. Turbulence mixing and temperature fluctuation of hot and cold fluids in tee pipes[C]// Advances in Fluid Modeling and Turbulence Measurements – Proceedings of 8th International Symposium on Flow Modeling and Turbulence Measurements. Tokyo：Nihon University， 2015：635-642. DOI：10.1142/9789812777591_0077.

[2] SHIGETA A， NAKAMORI K， SENDA M， et al. Thermal and hydraulic characteristics in a mixing tee pipe with fluid temperaturefluctuation[J].Science and Engineering Review of Doshisha University， 2008， 49：127-133. DOI：10.1299/jsmekansai.2008.83._8-24_.

[3] KAMIDE H， IGARASHI M， KAWASHIMA S， et al. Study on mixing behavior in a tee piping and numerical analyses for evaluation of thermal striping[J]. Nuclear Engineering and Design， 2009， 239（1）：58-67. DOI：10.1016/j.nucengdes.2008.09.005.

[4] CHAPULIOT S， GOURDIN C， PAVEN T， et al. Hydro-thermal-mechanical analysis of thermal fatigue in a mixing tee[J]. Nuclear Engineering and Design， 2005， 235（5）：575-596. DOI：10.1016/j.nucengdes.2004.09.011.

[5] AYHAN H， SOKMEN C N. CFD modeling of thermal mixing in a T-junction geometry using LES model[J]. Nuclear Engineering and Design， 2012， 253：183-191. DOI：10.1016/j.nucengdes.2012.08.010.

[6] HOWARD R J A， SERRE E. Large eddy simulation in Code-Saturne of thermal mixing in a T-junction with brass walls[J]. International Journal of Heat and Fluid Flow， 2017， 63：119-127. DOI：10.1016/j.ijheatfluidflow.2016.09.011.

[7] FERRARA P， DI MARCO P D. CFD analysis of turbulent heat transfer and thermal striping phenomena in T-junctions with liquid sodium[J]. Journal of Physics：Conference Series， 2017， 796：012009. DOI：10.1088/1742-6596/796/1/012009.

[8] SELVAM P K， KULENOVIC R， LAURIEN E. Large eddy simulation on thermal mixing of fluids in a T-junction with conjugate heat transfer[J]. Nuclear Engineering and Design， 2016， 284：51-63. DOI：10.1016/j.nucengdes.2014.12.025.

[9] SELVAM P K， KULENOVIC R， LAURIEN E， et al. Thermal mixing of flows in horizontal T-junctions with low branch velocities[J]. Nuclear Engineering and Design， 2017， 322：32-54. DOI：10.1016/j.nucengdes.2017.06.041.

[10] SELVAM P K， KULENVIC R， LAURIEN E. Experimental and numerical analyses on effect of increasing inflow temperatures on flow mixing behavior in a T-junction[J]. International Journal of Heat and Fluid Flow， 2016， 61：323-342. DOI：10.1016/j.ijheatfluidflow.2016.05.005.

[11] GAUDER P， SELVAM P K， KULENVIC R， et al. Large eddy simulation studies on influence of turbulent inletconditions on flow behavior in a mixing tee[J]. Nuclear Engineering and Design， 2016， 298：51-63. DOI：10.1016/j.nucengdes.2015.12.001.

[12] ZENG C， LI C W. A hybrid RANS-LES model for combining flows in open-channel T-junctions[J]. Journal of Hydrodynamics：Ser B， 2010，22（5）： 154-159. DOI：10.1016/S1001-6058（09）60186-4.

[13] KRUMBEIN B， TERMINI V， JAKARLIC S， et al. Flow and heat transfer in cross-stream type T-junctions：A computational study[J]. International Journal of Heat and Fluid Flow， 2018， 71：179-188. DOI：10.1016/j.ijheatfluidflow.2018.03.013.

[14] CHANG C Y， JAKARLIC′ S， DIETRICH K， et al. Swirling flow in a tube with variably-shaped outlet orifices：An LES and VLES study[J]. International Journal of Heat and Fluid Flow， 2014， 49：28-42. DOI：10.1016/j.ijheatfluidflow.2014.05.008.

[15] GRITSKEVICH M， GARBARUK A， MENTER F. A comprehensive study of improved delayed detached eddy simulation with wall functions[J]. Flow Turbulence Combust， 2017， 98：461-479. DOI：0.1007/s10494-016-9761-2.

[16] 余匯涛， 刘海鑫， 杨威， 等. T型三通管冷热流体混合过程的热疲劳特性数值模拟[J]. 武汉理工大学学报， 2016， 38（8）：49-55.

（编辑 武晓英）