基于GASA混合算法的支持向量回归机在需水预测中的应用
2019-07-08赵晓东李文竹刘心
赵晓东 李文竹 刘心

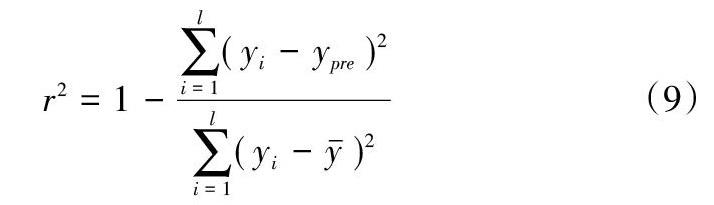

摘要:水资源需求预测是优化调度的基础,为供水系统提供了决策支持。本文以校园用水为例,提出了运用遗传和模拟退火组合算法(GASA)优化支持向量回归机(SVR)参数,建立GASA-SVR预测模型,用于校园日用水需求预测。利用SPSS软件进行因子分析,确定校园用水的影响因素并将其作为输入层,以均方根误差(RMSE)和相关系数(r2)作为评价标准,结果同BP神经网络(BP-ANN)、GA-BP-ANN、SVR模型进行了比较。实验结果表明,GASA-SVR模型 RMSE值较小,拟合度r2较好,因此,所提出的GASA-SVR模型是日常用水需求预测的有效工具。
关键词:需水预测;支持向量回归机(SVR);遗传算法;模拟退火算法;日用水量;因子分析
中图分类号:TV214 文献标识码:A
文章编号:1009-3044(2019)13-0195-04
Abstract: As the basis of optimal dispatching, prediction of the water resource demand can provide decision for water supply system. Taking campus water use as an example, this paper proposes to optimize SVR parameters by using chaotic GASA algorithm and establishes GASA-SVR predicting model for daily campus water demand. Analysis of influencing factors was carried out with SPSS software to determine the input of the model. Root mean square error (RMSE) and correlation coefficient (r2) were used as evaluation criteria. Compared with BP-ANN, GA-BP-ANN and SVR models, the results show that the GASA-SVR model has the smallest RMSE and the best r2. Therefore, the GASA-SVR model is proposed an effective tool for prediction of daily water demand. It is better than the other models commonly used.
Key words: prediction of water demand; support vector regression (SVR); GA; SA; Daily water demand; Factor analysis
1 引言
供水系统的自动化运营是将来供水发展的一个趋势,而要实现这个目标,就需要通过建立准确的水需求预测模型来控制泵站的最优总体数量以及最优泵调度。目前国内外需水预测方法主要分为时间序列法、结构分析法和系统方法[1,2,3]。近年来,研究者还利用一些研究方法,如人工神经网络、细胞自动机、蚁群算法、进化算法等,通过“拟物”或者“仿生”模拟自然现象来解决问题,已在人工智能、机器学习、数据挖掘等领域发挥了巨大的作用。支持向量回归机(SVR)由Vapnik等人[4]提出,是以统计学为基础的理论,它比传统时间序列预测模型有更好的预测效果[5],改善了神经网络容易出现的局部最优问题[6]。SVR预测方法已经成功应用于许多领域,如金融(股票指数和汇率)预测[7][8],短期光伏发电预测[9],工程与软件领域的产值和可靠性预测等。这些文献中,用SVR进行需水预测的文章比较少,对SVR三个超参数进行组合优化也很少,GASA混合算法可以利用SA算法的优势,在寻优过程中跳出局部最小值,逼近全局最优值,再利用GA算法的变异过程来提高最优值的搜索能力。鉴于此,本文通过遗传和模拟退火组合优化算法(GASA)对SVR的三个参数C,ε和σ进行寻优,建立GASA-SVR预测模型,并对用水影响因素进行因子分析,将关联度高的特征值作为GASA-SVR模型的输入,该方法在需水预测领域具有一定的泛化和指导意义。
第二主成分方差贡献率最大为:24.908%,通过线性方程所得特征向量分析为,主成分[F2]与平均气温[X1]、最高气温[X2]、最低气温[X3]相关性较低,与人数[X4]有较大的正相关,说明人数的增多直接影响到用水量的增长。
从以上分析可知,两个主成分F1和F2能很好的描述各影响因子跟用水量之间的关系,因此,将这两个主成分作为GASA-SVR预测模型的输入。
4 实验仿真
4.1 数据划分
为提高系统模型的预测精度和泛化能力,本文将这1035组原始数据进行如下处理:
1. 进行归一化,消除影响因素和目标用水量的量纲差异。得出结果后再进行反归一化得到所预测的日用水量。
2. 將原始数据组划分为训练集和测试集,分别为1005组和30组。
4.2 不同对比预测模型的参数初始化
本文将GASA-SVR的预测结果同SVR、BP-ANN和GA-BP-ANN进行对比,其中遗传算法和模拟退火算法的初始值如表3和表4:
对比模型中,SVR模型的超参数C,ε和σ的默认值分别为50,0.2,0.001,核函数选取径向基核函数,[σ]取0.001。所采用的ANN结构为常用的BP单隐层网络结构,因为单隐层BP神经网络可以以任意精度拟合函数[11],隐层神经元采用Sigmoid函数,默认隐层神经元10个,第一层学习率为0.5,第二层学习率为0.03,训练次数为100。
4.3 仿真结果与讨论
本文仿真用Spyder开发环境下的Python 3.6软件,分别对GASA-SVR、SVR、BP-ANN、GA-BP-ANN四个模型对校园用水量进行预测,图3为四种预测模型的仿真曲线比较:
四个模型分别用1005组数据进行训练,用剩下的30个数据进行测试验证。从图3中明显可以看出,GASA-SVR预测模型与实际日用水量曲线最为接近,特别是经过GASA组合优化超参数,可有效避免陷入局部最小值,得到GASA-SVR的三个超参数[C],[ε]和[σ]的值分别为4.5,0.05和0.01,精度提高了近3%,相对于BP-ANN和GA-BP-ANN具有明显的优势。
从表5中可以看出四种模型的平均相对误差、均方根误差、r2系数和平均绝对误差的比较,GASA-SVR的各项指标均优于其他四个模型,拟合度系数达到了0.927034。
5 结束语
a.本文运用GASA组合算法优化SVR的三个超参数进行需水量预测,分别建立GASA-SVR、SVR、BP-ANN、GA-BP-ANN四个模型进行拟合度对比,解决了传统超参数局部寻优而不是全局最优的问题,该模型可作为需水量预测领域的一个高效的替代方案。
b.运用SPSS软件分析用水影响因素,选择关联度较高的特征值作为输入,这样比传统单一使用历史用水数据作为输入更具有科学性。
c.本文建立的模型虽然提高了预测精度,但在运行时间上比其他模型要长,在现实生活中若把它们结合起来进行组合预测,将会有更广阔的发展前景。
参考文献:
[1] 袁伟,陈晓东.基于GA-BP神经网络与LSSVM支持向量机的日用水量组合预测模型[J].水电能源科学,2015,33(10):33-37.
[2] Herrera, Manuel1( mahefe@gmmf.upv.es);Torso, Luís2;Izquierdo,Joaquín1;Pérez-García, Rafael1.Predictive models for forecasting hourly urban water demand. [J].Journal of Hydrology.2010,Vol.387(No.1-2):141-150.
[3] 黄国如,李彤彤,王欣,等.基于系统动力学的海口市需水预测分析[J].水电能源科学,2016,34(12):1-5+40.
[4] 邓乃扬,田英杰.数据挖掘中的新方法:支持向量机[M].科学出版社,2004.
[5] Kwon, Hyun-Han; Kim, Min-Ji; Kim, Oon Gi. A Development of Water Demand Forecasting Model Based on Wavelet Transform and Support Vector Machine[J].Journal of Korea Water Resources Association.2012,Vol.45(No.11):1187-1199.
[6] 贾晓光.基于支持向量机的税收预测算法研究[J].电脑知识与技术,2018,14(02):242-245.
[7] Salim Lahmiri. Minute-ahead stock price forecasting based on singular spectrum analysis and support vector regression[J].Applied Mathematics and Computation.2018:444-451.
[8] Kazem, A; Sharifi, E; Hussain, Farookh Khadeer; Saberi, Morteza; Hussain, Omar. Support vector regression with chaos-based firefly algorithm for stock market price forecasting[J].Applied Soft Computing.2012,13(2):947-958.
[9] 陳锦铭,郭雅娟,伍旺松,等.基于数据预处理与特征表示的多核SVM短期光伏发电预测[J].水电能源科学,2018,36(09):205-208+147.
[10]员永生,马天,章立军,等.两种基于支持向量机的时间序列数据建模[J].电脑知识与技术,2016,12(19):241-246.
[11] 张维敏.两种需水预测影响因素分析方法的比较[J].人民珠江.2017,(3):29-31.
【通联编辑:梁书】
