微机械陀螺振动失效机理及可靠性设计研究

何春华,赵前程,杨振川,张大成,闫桂珍

(1.北京大学微电子学研究院微米/纳米加工技术国家级重点实验室,北京 100871; 2.美的集团,广东 佛山 528311)

工业级应用通常要求陀螺耐受0～2 kHz、总均方根为6gn～20gn的加速度振动,而军用领域可能要求陀螺耐受0～10 kHz、总均方根为30gn的加速度振动,而较大的振动应力可能会引发粘附、机械疲劳、结构断裂、性能退化、引线断裂等问题[1-2]。

由于MEMS陀螺一般采用滑膜驱动梳齿,并且设有阻挡结构,因此基本可避免大振动引发的结构吸合和粘附问题。宾夕法尼亚大学曾对MEMS硅谐振器进行高周疲劳测试,结果表明,单晶硅或多晶硅材料均会发生高周疲劳[3-4]、导致谐振频率下降。谐振频率约11 kHz的硅谐振器在经历107次振动循环后,其频率最大变化约为1%[5]。22.5 GPa应力下,1.56×109个振动周期后谐振器结构发生裂纹扩展[6],可见高振动应力下,结构发生材料疲劳,裂纹随着应力施加而不断扩展,进而影响谐振频率,应力越大,疲劳退化时间越短。意大利都灵理工大学也进行了振动试验,结论也类似[7]。为此,奥本大学提出了一个优化设计工具来提高结构的抗振能力[8]。考虑到陀螺也是一个谐振器,当周期变化的静电驱动应力和机械应力长期共同作用在结构上时,可能会加速结构疲劳、最终发生断裂失效。

实际应用环境中往往同时存在热应力和机械应力,机械振动应力的影响在高温或温循环境下会被增强,温度和振动复合应力可加速暴露器件的可靠性问题。加州大学欧文分校曾对MEMS IMU进行力热环境适应性研究[9],结果表明,立方体IMU结构在25 ℃～90 ℃环境变化或10 Hz～20 kHz振动条件下会发生0.2mrad的倾斜。2017年奥本大学对MEMS陀螺开展55 ℃高温与14gn机械振动的复合环境应力测试[10],结果表明复合环境应力会加速标度因子和零偏退化。此外,华南理工大学和工信部电子五所指出,若机械振动或冲击的应力较大,键合引线也可能会发生断裂失效[11]。

鉴于目前国内外对MEMS陀螺谐振器的振动特性和失效机理研究报道较少,对复合环境应力下MEMS陀螺可靠性的研究也较少,因此本文将开展相关理论、仿真和试验研究,以评估陀螺的薄弱环节、并提出有效的抗振设计方法。

1 微机械陀螺振动试验设计

产品在服役过程中往往受到复合环境应力的影响(如振动和温度等),虽然单个应力量值小于极限应力,但由于多种应力之间存在耦合作用,更容易暴露产品的缺陷,因此本文将采用复合环境应力试验方案,通过高加速极限试验(HALT)来快速暴露陀螺的缺陷。振动试验主要包括正弦振动和随机振动试验,考虑到随机振动比正弦振动更接近实际情况,能更有效考核产品的耐振能力、快速暴露产品的缺陷和薄弱环节,因此选用随机振动应力进行试验。采用图1所示的HALT试验箱同时施加3轴随机振动和高温应力,试验时陀螺上电工作,每次试验时间至少为15 min,最长不超过12 h。陀螺的谐振频率约为8 kHz,品质因子Q值约为2 000。

为了实时监测MEMS陀螺的振动疲劳特性,本文开发了LabVIEW专用测试软件,结合NI PXI 4461模拟采集卡进行驱动交流信号dac和驱检信号dso的实时采集,软件如图2所示。考虑到PCB会影响陀螺的振动特性[12],因此为了更好评估陀螺表头的本原振动特性,用502胶水把陀螺表头固定在振动台上,而电路板放在振动台外面,表头与振动台之间通过导线软连接,这样可有效去除PCB板对陀螺振动的影响,如图1所示。

首先,设置随机振动的加速度总均方根为20gn,振动频率为0～2 kHz,环境温度控制为80 ℃高温。试验进行12 h后,dac与dso波形、谐振频率均正常,如图2所示,陀螺未见发生振动疲劳失效。接着,增大环境应力,设置随机振动的加速度总均方根为30gn,振动频率为0～10 kHz,环境温度仍为80 ℃高温,更换新的陀螺进行HALT试验。试验测试约2 h后发现陀螺无法正常工作,如图3所示,dac与dso波形、谐振频率均失效。失效后停止随机振动,试验箱恢复室温后再次上电测试,陀螺依旧无法正常工作,因此认为陀螺已失效,需通过无损或有损方法进行失效分析和定位。

图1 基于Halt试验箱进行复合环境应力试验

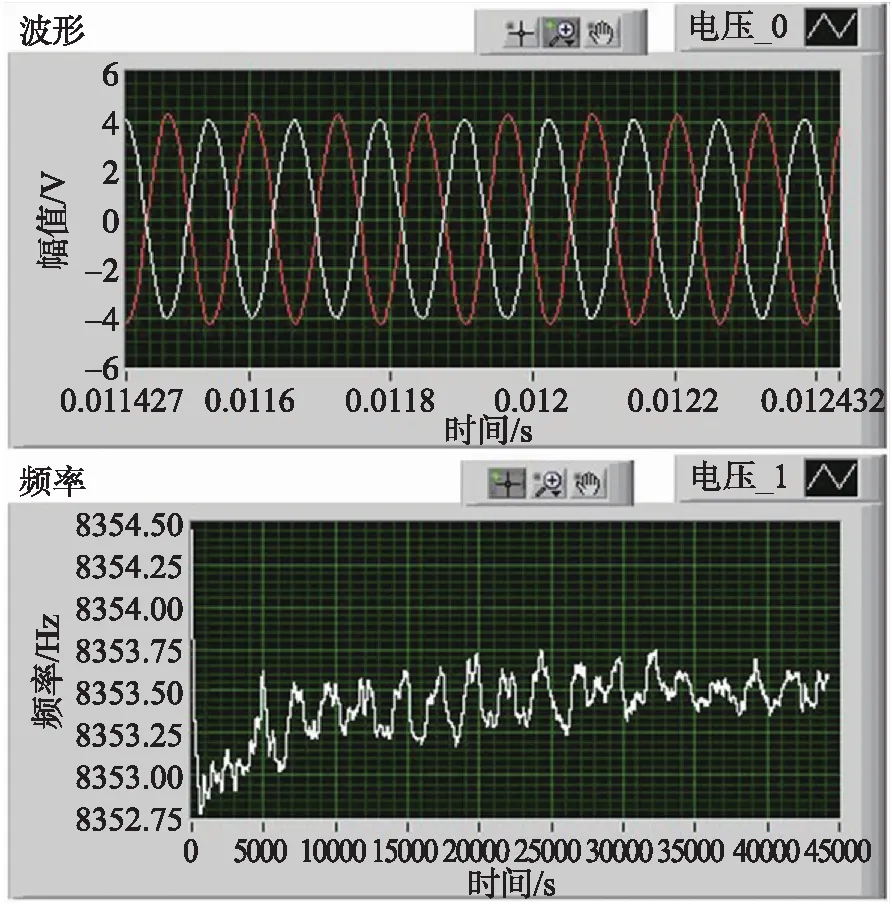
图2 驱动波形及谐振频率实时监测结果

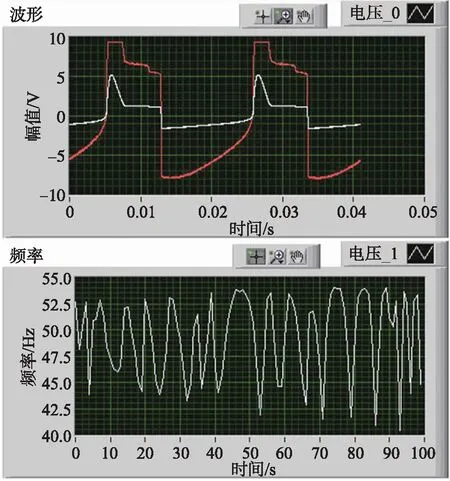
图3 强化环境应力试验后陀螺失效波形图

2 失效模式分析

复合环境应力试验后陀螺驱动轴扫频结果如图4所示,可见器件扫频结果异常,器件无法谐振,因此初步诊断失效模式为陀螺机械结构断裂或者金丝引线断裂。接着,采用德国YXLON的三维立体成像X射线显微镜(Y. CT Precision S)对MEMS陀螺进行透视分析,如图5所示,通过3D X-Ray照片可从不同角度观察内部结构,分别得到俯视图、左视图和前视图,并且可以重构出内部结构的三维形貌。图中可清晰看见金属引线以及引线键合点,并且可观察到引线在键合点处断裂。由于硅的密度与空气接近,因此难以观察清楚硅结构是否完好,需开封后进一步检查确定。通过3D X-Ray预分析,确定了封装结构形状和芯片的大体位置,为后续高质量的开封提供了重要的指导,可有效防止开封过程中引入新的失效信息污染原始失效信息。

图4 复合环境应力试验后陀螺驱动轴扫频结果

图5 MEMS陀螺的3D X-Ray失效分析

在超净环境下采用精密金属切割机对陀螺管壳进行开封,如图6所示。开封后利用金相显微镜对陀螺进行内部目检分析,观察发现硅结构质量块和弹簧梁均完好无损,没有出现断裂,但有一根引线在键合点处发生断裂,如图7所示,因此可判断陀螺失效是由引线断裂引起,为深入探究金丝引线断裂机理,应对其进行理论推导和仿真分析。由于金丝引线为双端固支,因此分析前需先确定引线的参数。经SEM显微镜测量可知,断裂的引线长度约为3 mm,直径为24 μm。

图6 采用精密金属切割机对陀螺管壳进行开封

图7 陀螺部分结构的金相显微结果

3 失效机理分析

弯曲引线的示意图如图8所示,其参数分布振动方程为[13]:

(1)

其中N为轴向外力,F为横截面方向的外力,L为引线长度,d为引线直径,A为引线横截面积,ρ为密度,E为杨氏模量,I为截面惯性矩,c为阻尼力系数,W为横截面上的挠度。由于上述偏微分方程非常复杂,要求其解析解必须做一定的简化和假设。本文考虑直线情况,基本假设如下:①x轴为中性轴,无拉伸与压缩;②保持平面假设,即引线变形前后其横截面与中性轴垂直,忽略剪切形变的影响;③材料是线弹性的,引线各向同性;④相对x方向的应力,y和z方向的应力可忽略;⑤忽略转动惯量的影响;⑥忽略轴向外力N的影响,并且假设EI为常数。

图8 弯曲引线的示意图

上述参数分布模型的齐次方程为:

(2)

通过分离变量法可求解以上方程,令:

W(x,t)=X(x)T(t)

(3)

其中X(x)与t无关,表示振型;T(t)与x无关,表示随时间变化的振幅。代入式(2)可得:

(4)

由于上式左边与时间无关,右边与位置无关,则它们的值应该为常数,假设该常数为α4(为了不得到平庸解,α为非0常数),则有:

X(4)(x)-α4X(x)=0

(5)

T″(t)+2ξωT′(t)+ω2T(t)=0

(6)

X(x)=D1sin(αx)+D2cos(αx)+D3sinh(αx)+D4cosh(αx)

(7)

D1、D2、D3、D4为常数。假设金丝引线满足欠阻尼振动,则方程(6)的齐次解为:

(8)

由于金丝引线双端固支,引线两端的位移和速度都为0,因此有边界条件:

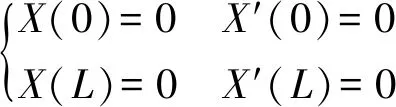
(9)

求解可得D2=-D4,D1=-D3,并且有:

(10)

上式二元一次线性方程组存在解的条件是系数的行列式为0,即:

(11)

化简行列式可得:

cos(αL)cosh(αL)=1

(12)

求解该超越方程可得:

αiL=4.73,7.85,10.996,14.14,… (i=1,2,…)

(13)

(14)

由式(10)可得:

(15)

Xi(x)=D1{[sin(αix)-sinh(αix)]+Bi[cos(αix)-cosh(αix)]}

(16)

根据叠加法,参数分布模型的振型函数为:

(17)

(18)

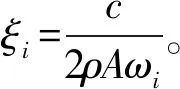
T(0)=0,T′(0)=0

(19)

推导可得:

(20)

(21)

因此,金丝引线在外界加速度作用下振动位移的表达式如下:

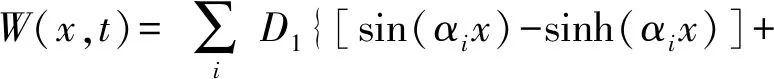
(22)

同理,通过偏微分可求得加速度为:

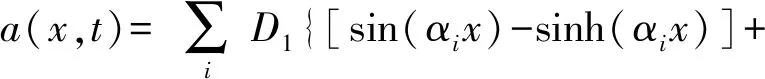
(23)

则金丝引线受到的作用力为:

(24)

通过求导可知,无论是瞬态项还是稳态响应项,当满足ω0≈ωi时,响应加速度的幅值最大,并且稳态项与瞬态项的相位相反。考虑稳态振动情况,当ω0≈ωi,引线受到的最大作用力约为:

(25)

即当外界振动力频率与引线固有频率接近时,引线将发生稳态共振,外界振动力将被放大Qi倍,被放大的振动力可能会导致引线断裂。考虑到引线的剪应力远小于正应力[14],因此本文主要以正应力来分析其抗振能力,当引线谐振时,引线受力截面的最大正应力σwire_max为[14-15]:

(26)

其中,Mwire_max为最大弯矩,u=d/2为表面距离中性层的距离。引线截面惯性矩为I=πd4/64,横截面积A=πd2/4,考虑集总模型,则上式可化简为:

(27)

根据上式可知σwire_max与ρL2Qi成正比、与d成反比,因此可通过缩短引线长度、增加引线直径和阻尼来降低振动应力。通过对比最大应力与引线材料的抗拉强度即可分析引线的抗振特性。事实上,影响引线抗振特性的因素较多,本文采用的最大应力分析法虽然并非最精确的分析方法,但其分析结果比较接近或逼近实际情况,可对失效分析和可靠性设计起关键的指导作用。另外,对于金属引线,在引线键合点的结构突变处容易发生应力集中,若振动应力较大,将容易导致引线断裂。

把陀螺表头中金丝引线看作为一根双端固支的直线,前面测量得到引线长度L=3 mm,直径d=24 μm,面积A=πd2/4,金的杨氏模量E为78.5×103MPa,密度ρ为1.93×10-14kg/μm3,截面惯性矩I=πd4/64。因此,根据式(14)可计算出前三阶固有频率分别为4 787.57 Hz、13 197.11 Hz、25 871.53 Hz。为了验证理论分析的正确性,本文利用ANSYS软件进行建模仿真分析,如图9所示,通过仿真得到的前三阶固有频率分别为4 783 Hz、13 179 Hz、25 822 Hz,与理论计算结果基本一致,因此验证了理论推导的正确性。

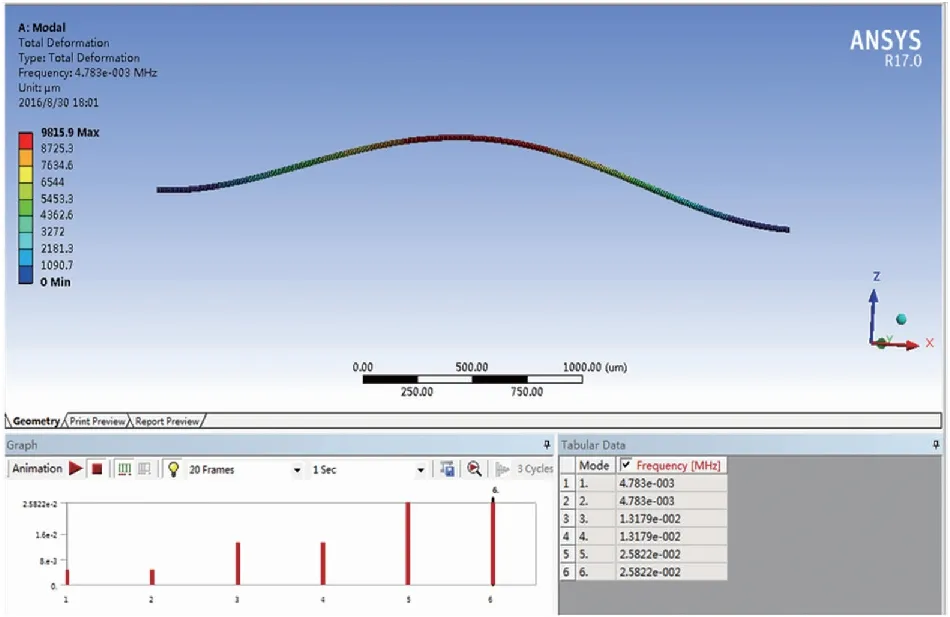
图9 基于ANSYS对引线进行模态仿真

由于陀螺固有频率在8 kHz和9 kHz之间,驱动谐振频率为8 697.29 Hz,检测谐振频率为8 721.73 Hz,而金丝引线一阶固有频率为4 787.57 Hz。对于频率范围为0～2 kHz、总均方根为20gn的振动加速度,由于陀螺结构和金丝引线的固有频率都在振动频率范围之外,因此几乎不响应外界加速度信号,即外界振动难以使其发生断裂。但对于振动频率为0～10 kHz,总均方根为30gn的振动加速度来说,陀螺结构和引线的固有频率均在振动频谱内,因此会响应外界加速度而发生共振。由于陀螺结构本身按谐振设计,外界振动应力对梁和锚点的影响较小,但金丝引线没有考虑谐振设计,因此影响较大。当Qi为100时,根据式(27)可算得引线最大应力约为213 MPa,大于金丝引线的抗拉强度200 MPa,此时还叠加高温热应力,则引线会加速断裂。

4 可靠性设计及验证

尽管降低品质因子可使引线最大应力小于抗拉强度,但若引线发生共振,则高周振动疲劳也会导致引线断裂。因此,要提高引线的抗振能力,最简单的方法是提高引线的一阶固有频率,使其值高于外界最大振动频率(如2 kHz或10 kHz)。根据式(14)可得:

(28)

因此,要提高固有频率,可通过增大引线直径和缩短引线长度来实现。此外,根据式(27)可知,增大引线直径和缩短引线长度还可降低引线应力,有利于提高抗振能力。综合考虑,为节省成本,优先选择缩短引线长度方案。因此,优化设计时可以把引线长度由3 mm改为2 mm,其他参数不变。根据式(28)可算得引线的一阶固有频率由4 787.57 Hz升至10 772.03 Hz、大于外界最高振动频率10 kHz,避免了引线谐振;此外,根据式(27)可算得谐振时引线最大应力由213 MPa下降至95 MPa、小于金丝抗拉强度200 MPa,可见通过缩短引线长度可有效提高引线的抗振能力。

为了验证上述分析的正确性,我们对新的陀螺样品进行同样的强化应力试验,该陀螺样品中同时存在2 mm和3 mm长度的金丝引线。振动2 h后,陀螺同样失效、无法起振。失效分析发现陀螺的硅结构和引线键合点均完好无损,但3 mm长度的金丝引线发生断裂,而2 mm长度的金丝引线未发生断裂,如图10所示,因此验证了理论分析的正确性。此外,增大引线直径也可有效提高抗振能力,原理类似,这里不再赘述。

图10 短引线完好无损,但长引线的根部断裂

5 结束语

针对复合环境应力试验的MEMS陀螺失效品,本文开展了详细的失效定位和机理分析,推导了引线的振动响应特性和固有模态,并提出了引线的抗振设计方法。仿真分析验证了引线固有模态理论推导的正确性,实验结果表明,通过缩短引线长度可有效提高引线的固有频率和降低振动应力,从而增强其抗振能力。优化设计后陀螺可耐受频率为0～10 kHz、总均方根为30gn的加速度随机振动。