基于贝叶斯统计方法的多重液相色谱-质谱试验数据匹配研究

崔 健

(中国石油大学胜利学院 基础科学学院,山东 东营 257061)

液相色谱-质谱联用仪(LC-MS)是由液相色谱仪与质谱仪结合而构成的分析仪器,它结合了液相色谱仪有效分离热不稳性、高沸点化合物的分离能力与质谱仪很强的组分鉴定能力,是一种分离分析复杂有机混合物的有效手段[1],是发现并分析生物标志物中复杂肽信号的关键技术[2]。为了得到肽链更准确信息,部分试验采用二级质谱联用(MS/MS),通过碰撞诱导解离给出化合物的碎片离子等结构信息,能量越大打成的碎片越多。由低级别离子对肽链成分进行进一步分析,可以降低对质谱的要求,能够获取到肽链组成、准确的电荷数目及时间等信息。在实际操作中,为了提高肽链检测覆盖率及量化准确度,经常采取对相同样本的多次重复试验[3],理论上同种肽链在不同次试验中应该出现在相同LC时间与M/Z位置,试验谱图应该是一致的[4]。但是,由于试验误差不可避免,谱图普遍存在时间偏移的情况,因此需要对多个谱图进行校准[5]。目前,比较通用的软件如Quil[6]、proteinquant[7]、msinspect[8]、OpenMS[9]和superhirn[10]等对于重复试验数据校准基本为整体时间谱图校准。对于复杂谱图,例如较小的时间窗口中产生多个LC峰的情况,这样时间修正就会存在修正错误的问题。因此,本次研究采用二级质谱联用(MS/MS)获取的肽链信息作为训练序列,通过Warping函数来进行时间校准,并联合使用贝叶斯统计方法对Warping函数进行提升,对任意峰对给出相关信号概率及非相关信号概率,并验证有效性。最后,将多个数据的肽链信号对通过该方法进行校准匹配,并验证覆盖率。

1 数据分析

1.1 数据来源

处理数据由RCMI Proteomics and Protein Biomarkers Cores试验室产生,经过LTQ OrbitrapVelos仪器处理的一组TAGE肿瘤样本。LC-MS试验是将蛋白质切割成肽链,并使用试剂利用肽链斥水性不同的特性,将其冲入到质谱仪中。斥水性不同导致肽链进入质谱仪形成谱图的时间就不一致,形成了不同肽链时间上的区分。进入质谱仪中的肽链将随机带上电荷,根据不同肽链大小、质量、带电荷不同的特性,形成的质量与电荷比(M/Z)值不同,形成质荷比维度的区分。同一种肽链由于具备相同斥水性及质荷比,因此理论上将出现在谱图中的一个特定位置上,此类谱图为Level 1数据(图1)。由于仪器操作等影响,为了提高精度,一般将进一步进行MS/MS试验,即从Level1谱图中随机选取位置,将肽链进行成分分析确定肽链组成,称为Level 2数据。

图1 数据1谱图

本次研究从多组试验中选取了两组数据(数据1与数据2)进行分析,由MS/MS检测到肽信号信息(图2)。

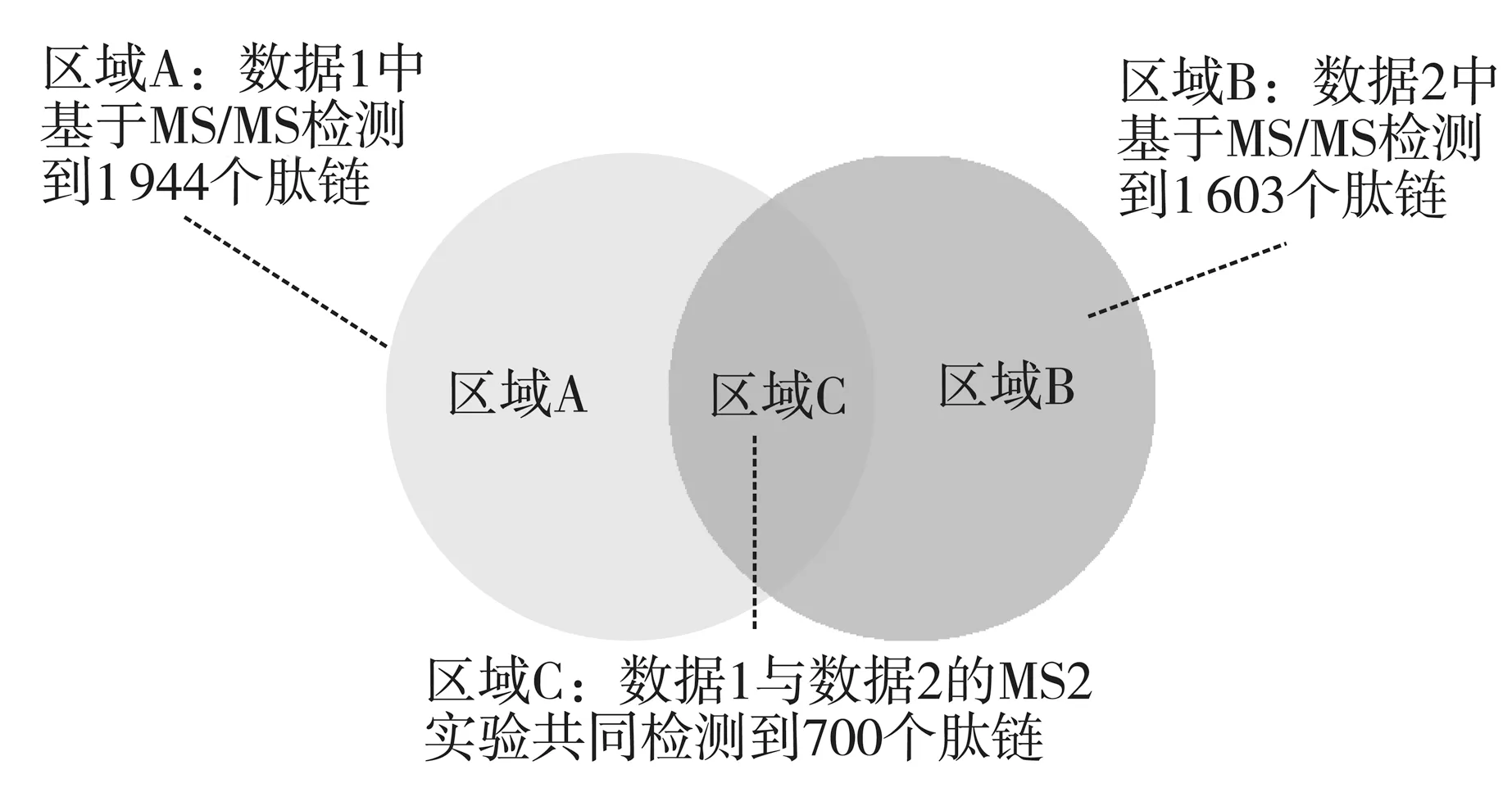
图2 MS/MS检测结果韦恩图

1.2 数据处理

数据处理分为“数据预处理”、“训练与测试数据集生成”、“Warping函数及贝叶斯统计方法建模”、“模型验证及全集校准”四个部分。

1.2.1 数据预处理

在数据预处理中,根据MS/MS信息表,生成肽信号合集,并计算肽链荷质比(M/Z值),以肽链M/Z值为中心,前后20×10-6宽度,计算LC谱图,生成肽链的全时间段XICs(图3)。然后,在全时段XICs上进行区间检测。

图3 肽链“CSTSSLLEACTFR”全时段XICs

1.2.2 训练与测试数据集生成

生成训练和测试数据集的原则是肽链信号必须具备可验证的真实值(ground truth)。由MS/MS检测到的肽信号即为真实信号,其具有的M/Z值与时间值即为真实可靠的值。因此,选择图2交集部分(共700个肽链)作为训练与测试数据集。在训练测试数据集中,首先进行区间检测预处理,能够检测到的区间,即具备较好的峰值。区间包含MS/MS时间点即为可用肽链。经过区间检测预处理,共599个肽链可用。采用2-折交叉验证,即随机选取一半作为训练,一半作为测试。训练序列用于warping函数与贝叶斯统计模型的生成,测试序列用于测试模型产生的肽信号匹配结果的准确性(以MS/MS检测值作为真实数据)。

1.2.3 Warping函数及贝叶斯统计方法建模

对于生成的训练序列,选取由MS/MS确定的相关信号时间对生成Warping函数。在使用Warping函数拟合之前剔除偏差较大的奇异点。采取每个训练序列肽信号的数据1时间减去数据2时间,然后计算方差,采用平均值±3倍标准差作为标准,将外部的点去掉,直方图如图4所示。

图4 时间差直方图

然后采用四阶多项式作为Warping函数拟合,生成多项式参数，拟合后如图5所示。

图5 Warping函数拟合结果

下一步将计算由MS/MS检测结果确定为相关信号的时间对、确定为非相关信号的时间对,分别距离Warping函数的时间差值,如图6所示。

分别对相关信号时间差值和非相关信号时间差值建模。以相关信号时间差值建模为例,根据测试数据中的时间差,得到n个样本t(t1,t2,t3,…,tn),其中ti是测试序列中第i对信号的时间差值。通过对样本的直方图观察,基本符合正态分布特征,一般情况下正态分布的概率密度函数中包含的两个参数μ和σ由样本值进行最大似然估计。使用贝叶斯统计方法进行建模,首先设定先验信息(Prior),即将参数μ和σ看作为两个随机变量,其服从以下分布特征:

p(μ|σ2)～N(μ0,σ2/κ0),

图6 相关信号与非相关信号时间差直方图

根据贝叶斯公式,参数μ和σ的联合分布为

p(μ,σ2)=p(μ|σ2)p(σ2),

即为

简化一下即可得:

下一步进行后验信息(posterior)计算,

p(μ,σ2|t)=p(t|μ,σ2)p(μ,σ2),其中p(μ,σ2)为先验信息已经计算获得。

而p(t|μ,σ2)～N(μ,σ2)是μ和σ的正态分布。这样计算p(t|μ,σ2)得:

p(μ,σ2|t)∝σ-1(σ2)-(1+(ν0+n)/2)×

令

得

现在已知先验信息,后验信息如下:

(1)

p(μ|σ2,t)～N(μn,σ2/κn),

(2)

(3)

p(x|μ,σ2,t)～N(μ,σ2).

(4)

式中,x为任意时间差,为随机变量;t为已经获得的样本值,那么下一步将计算p(x|t)的值,这样就无须估算正态分布中μ和σ的值,直接由样本值t计算任意时间差变量x的分布。

将(1)、(2)、(4)代入以上公式得:

(5)

(6)

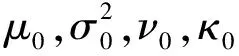
1.2.4 模型验证及全集校准

模型的建立及测试是在训练与测试数据集上进行的,即图2的区域C部分。随机选取一半作为训练序列建立以上模型,另一半数据验证模型的有效性,并与MS/MS检测的真实数据比对获取模型准确度。在验证模型有效后,对图2中区域A和区域B中的肽链信号通过模型进行匹配。区域A中信号为由MS/MS检测到的仅在数据1中有真实值的肽信号,通过模型匹配得到其在数据2中的匹配信号;同理,区域B中亦是如此。这样就完成全集的校准匹配,得到整体的匹配覆盖率。

2 结果分析与问题讨论

得到的结果主要有两部分,一是通过贝叶斯统计方法改进Warping函数校准匹配有效性结果;二是全集最终校准匹配结果。

2.1 模型有效性结果

本次研究进行了10次测试,每次从训练与测试序列中随机选取300个进行Warping函数拟合,然后计算时间差,并用贝叶斯统计方法训练建立模型。另外,299个作为模型测试,一是单独使用Warping函数,判断测试序列中时间距离Warping曲线最近的区间为匹配校准区间;二是使用改进的Warping函数与贝叶斯统计方法建立的模型,如果相关信号模型给出的概率大于非相关信号的模型概率,则判断为匹配。以上两种结果均与MS/MS时间点真实值进行比对,计算准确度如表1所示。

表1 测试结果对比

由表1看出,用Warping的测试结果准确性均值为86.81%,通过Warping函数联合使用贝叶斯统计方法建模准确率均值达到93.08%,提高了6.27个百分点。

2.2 数据全集的校准匹配

由MS/MS检测到的数据1与数据2的肽链共4 247个,分布如图2所示。交集共700个,通过区间检测的信号共599个,在此基础上采取Warping函数联合贝叶斯统计方法建模进行匹配。区域A中1 944个,区域B中1 603个,共3 547个肽链。根据模型给出的匹配与非匹配的概率大小,共能实现3 185个肽链在另外数据中的区间匹配,覆盖率达到89.8%。

2.3 问题讨论

基于以上研究结果,可以看出,交集的700个肽链中只有599个能被检测到信号区间,检测到区间的概率大约为85%。这说明部分被MS/MS检测到的肽链信号非常弱,无法在level1数据中被检测出来。这是由于区间检测不准确造成的,本文在区间检测中采用的是简单的低于最高峰值20%即在区间外的办法,很多情况下并不有效,检测不到真实的肽信号区间,因此,下一步将重点研究准确的区间检测算法。

3 结束语

采用Warping函数联合贝叶斯统计方法建模对多次重复的液相色谱-质谱数据进行时间校准,根据MS/MS检测值选取训练序列进行时间拟合。通过测试序列验证,单独使用Warping的测试结果准确性均值为86.81%;通过Warping函数联合使用贝叶斯统计方法建模准确率均值达到93.08%。同时,完成两个谱图的匹配校准,覆盖率超过89%。对下一步进行肽链量化提供了非常有意义的算法支撑。