水声被动测距技术及误差分析*

孔大伟 蔡昱明

（1.海军士官学校 蚌埠 233012）（2.92730部队 三亚 572016）

1 引言

水下航行的潜艇，为保证自身的隐蔽性，一般情况下不用主动声纳，声纳长时间处于被动工作状态。然而一般被动声纳并不具备目标测距功能，因而利用被动声纳进行测距一直是水声技术中的重点课题。20世纪七十年代国外开始研制被动测距声纳并装备潜艇，这种声纳除可测定有源目标方位外，还可测定其距离，从而为潜艇的隐蔽活动创造了有利的条件。被动测距声纳的出现是水声技术的一大突破，但由于受平台尺寸和技术条件的限制，其应用范围仅限于大尺寸基阵，测距精度也不高。本文从理论角度分析被动测距的原理和形成误差的原因。

被动测距方法分为方位法和时差法，其共同点是利用间距相当长的多个、两个或三个子阵。

2 方位法测距

方位法测距原理如图1所示。

A、B为两个方向性子阵，相距为D。利用两个子阵分别测出两个方位角α、β。由正弦定理可知有：

其中，r1、r2为目标S与两个子阵声中心的距离。因此可由α、β、D求出r1、r2，从而求得目标距离为

这一方法在远场平面波假设条件下利用各子阵测目标方位角，亦即要求子阵的尺寸小于r1、r2。此外D应足够大，否则α与β的差别太小，误差加大。一般来说，这一方法测距误差较大，因而被另一方法“时差法”所取代。

图1 方位法被动测距原理

3 时差法测距

时差法一般利用三个子阵，其机理是测量波阵面的曲率。此时假定目标是点源，声波按柱面波或球面波方式传播。如图2所示。设在直线上布放三个等间距的阵元或三个子阵，间距为d。要测量的是点声源目标M与中心阵元B的距离与方位角α。

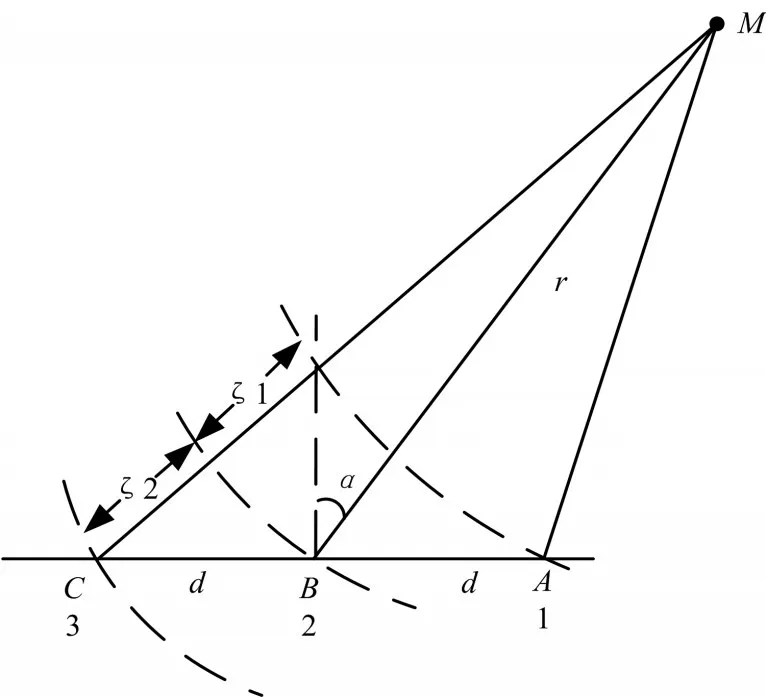
图2 三元阵被动测距几何关系

点源发出的声波到达阵元A、B、C的声程差ξ1、ξ2为

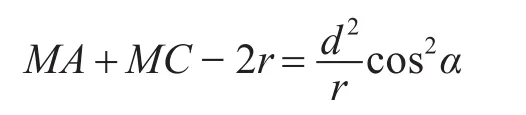
综合可得

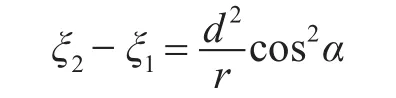
注意到ξ1＝cτ12，ξ2＝cτ23，而τ12、τ23为与程差ξ1、ξ2对应的时差，于是上式成为

由此得到目标距离r为

其中τd＝τ23-τ12为两个时差之差。因此，在已知阵元（或子阵声学中心）间距d、声速c时，测得ξ12、ξ23及角度α便可求出目标距离r。

α的测量则可利用远场平面波近似，因此有

4 时差法测距误差分析

本文从测距公式出发，研究随机因素引起的误差、系统误差及修正方法。

4.1 随机误差

假定各阵元布在一直线上，将

求全微分后得到测距相对误差

若各项误差彼此独立，则相对均方根误差为

这里Δα以弧度计。上式中第一项为阵元（或子阵）间距d的测量误差，当d达到几十米时，这项误差可做到小于0.1%。第二项为角度（或方位角）测量误差引起的相对距离测量误差。当α≤45°时，若Δα＝0.2°，这一误差小于0.7%，但当α很大，接近90°时，tanα急剧增大，因而这项误差很大，所以目前被动测距声纳只在α=±60°以内测距。第三项Δc/c为声速测量误差，通常可使其达到0.1%，因而影响不大。式中第四项Δτd/τd为时差之差测量误差，它与目标距离r有关；r越大，波阵面曲率半径越大，τd＝τ23-τ12越小。从本质上说，这是因为此时柱面波的条件已不满足。由此可知，被动测距不可能在远距离上进行，亦即远距离测距是不利的。

为说明Δτd的影响，单独考虑Δτd造成的误差。

由上式得

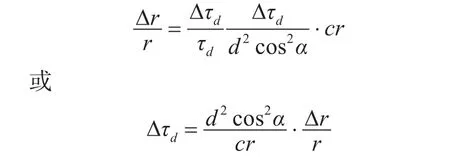
4.2 系统误差

现在分析一下系统误差对测距的影响。基阵安装误差会造成很大的测距误差，这是因为三个阵元或子阵不可能安装成一个绝对的直线，总是有偏离，它们之间的间距也不可能绝对相等，因此必须进行修正，以减小测距误差。

当三个阵元在一个直线上，但阵元位置有偏离时，则如图3所示。

图3 三元阵共一直线，阵元位置有偏差时的阵元配置

中间阵元不在1、3阵元连线的中心位置，而是偏离中心Δd。此时在计算距离时，如仍以1、3阵元连线中点为0点，则带来的测时误差为

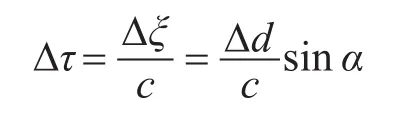
由图3可知，实测的τl2减小了Δτ，而τ23增大了Δτ，所以

可见只要安装误差为2mm就会带来很大测距误差。

当三个阵元不成直线时，考虑中间阵元在xoy平面内有一偏离，其坐标为B（x，y）。这里没有考虑垂直位置的偏离，因它不会引起程差的变化，如图4所示。

图4 三阵元不在一直线上，中间阵元有偏离时阵元配置

B点与o点（2号阵元）的程差为

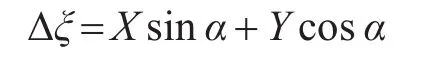
实际上各接收器之间的程差测量值为ξ′12、ξ′23，因而

所以

设舰艇首尾线在x轴上，中间阵元位于点（x，y，z）。为简化分析，设声源与基阵在同一深度，如图5所示。

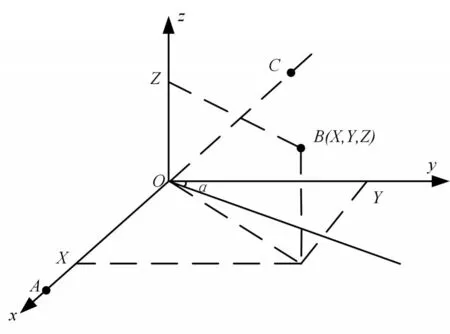
图5 阵元有偏离时的阵几何

在xoy平面内，声线与y轴夹角为α。

先考虑舰艇有横摇的情况。舰艇的横摇意味着基阵架绕x轴旋转ψf角（向右为正）。设地球坐标系为x′y′z′，阵元相对于地球坐标系的位置坐标如图6所示。

图6

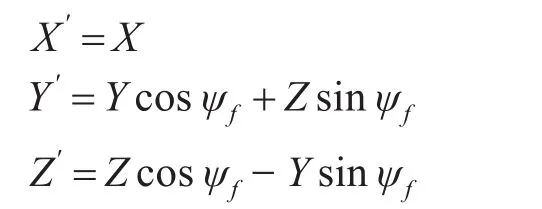
再考虑舰艇有纵倾的情况。此时基阵架绕y′轴转ψz（向上为正）。再设地球坐标系为x″y″z″一中间阵元B在此坐标系的位置如图7所示。

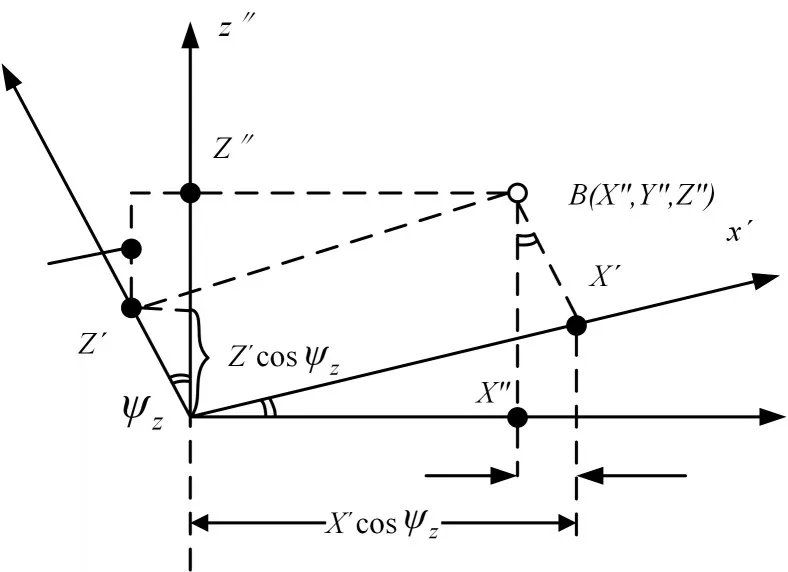
图7

这样可得到舰艇有纵横摇时，中间阵元在地球坐标系x″y″z″的位置为

中间阵元的位置变化将会带来附加的测距误差。由于舰艇摇摆，中间阵元所造成的附加程差为

实际进行测距计算时，必须按测得的横摇角ψf和纵倾角ψz，利用上式对每一方位角α进行修正。

5 结语

综上所述，分析可得，安装误差对测距误差影响非常大。

第一，安装误差对测距误差的影响随方位角α的增大而减小。我们知道，当tanα＝X/Y时，Δξ很大。特别当X＝Y，α＝45°时，Δξ最大。然而并不是在45°时，安装误差对r计算引起的误差最大。这是因为随着α的增大，实际测得的τd=τ′23-τ′12减小，致使安装误差造成的Δξ对距离计算的贡献增大。

第二，安装误差对远距离测距的影响比近距离大。这是因为远距离声波接近平面波，τd会很小。而当目标方位角α一定时，安装误差引起的Δξ不变，因而它对距离计算的影响相对增大，从而使测距误差增大。因此，大目标方位角和远距离测距是被动测距的最不利状态。

第三，考虑舰艇摇摆的影响。若三个阵元不在一直线上，舰艇又有纵横摇，将会使测距误差进一步增大。若X＝Y＝Z＝0，即无安装误差时，则Δξ＝0，舰艇摇摆不产生附加误差。若ψf＝0，ψz＝0，则Δξ＝Xsinα+Ycosα，即为仅有安装误差的情况。若既有ψf≠0，ψz≠0，且X、Y、Z≠0，由安装误差引起的测距误差则进一步扩大。