验前信息在武器装备试验中的应用研究*

戴家君 郑 锦

（1.92785部队 秦皇岛 066000）（2.91404部队 秦皇岛 066000）

1 引言

目前，武器装备试验一般采用的是“独立试验、集中测试、重点考核”的试验模式，这种试验模式使不同阶段界限明显，由不同的单位实施而被截然分开，浪费了大量的试验数据。并且组成武器装备系统的许多设备在参加系统试验之前都是经过单机试验的设备，在单机试验时储备了大量的试验数据。如果能够科学充分地利用这些验前信息，将会在不增加试验样本量的情况下，提高试验置信度。甚至在有的试验项目上可以减少试验样本量，降低试验成本。

本文将就武器装备系统试验时如何进行验前信息预处理加以探讨，主要研究验前信息的种类、验前信息分布类型及相容性检验。

2 验前信息的种类

对于武器装备系统而言，验前信息的种类根据获取方式不同，可以概括为以下几种。

2.1 单元及分系统试验信息

一般的武器装备系统均由若干单元和分系统组成。可以采用金字塔式评定方法，从底层单元出发，直至系统级，将信息一级一级向上折合，把对单元和分系统进行大量的试验数据综合利用形成验前信息。

2.2 不同环境下的试验信息

为了考核武器装备系统的环境适应性，系统经常需要在不同环境（如高海情）下进行试验，试验要求各组成单元或系统的失效机理不变，运用此类信息需要研究利用环境因子进行折算。

2.3 历史信息

包括武器装备系统警戒探测设备、各武器单机等分系统以往的各种试验信息。这些数据由于是在不同试验环境下得到的，并且可能是同一型号不同产品试验所得信息，如果直接引用的话缺少科学依据，必须经过环境因子折算、相容性检验等处理后，再结合现场试验进行解算。

2.4 仿真试验信息

武器装备系统中一些新指标体系中提出的指标，在以往试验中由于试验条件无法满足，一般不进行外场实兵考核，而是随着仿真技术日趋成熟，通过仿真手段来进行考核。所以通过仿真获得的验前信息也将成为武器装备系统信息来源的重要途径之一。

3 验前信息的预处理过程

对于不同种类、不同来源的大量验前信息，只有经过预处理之后才可直接应用到试验中，预处理过程是验前信息使用的关键过程。于各种各样的验前信息首先应确定其分布类型，然后进行相容性检验，确定和现场信息是否属于同一总体。

3.1 验前信息的表示

武器装备系统在利用不同来源的验前信息前，要把验前信息转换成分布函数来表示。对于不同来源、不同情况下的验前信息本文采用不同的确定验前分布的方法。

3.1.1 对由仿真而来的验前信息采用直方图法［1］

如系统某仿真试验中共记录n组数据，每组中又有mi(i=1，2，...，n)个数据，由各组数据得出的θ的评估水平，分别记为(i=1，2，...，n)，当n较大时，可由直方图法计算出仿真条件下系统θ的先验分布。将θ的可能范围分成一系列小区间，记区间个数为k，各区间长度分别为Li(i=1，2，...k)，计算落入每个区间的(i=1，2，...，n)个数，分别记为fi(i=1，2，...k)。

系统θ的先验分布：π(θ)=fi/nLi，(i=1，2，...，k)。

由上式可得系统θ的直方图形式的先验分布，另外也可在直方图上做一条光滑曲线，由光滑曲线得到的分布仍记为π(θ)。

3.1.2 对验前分布的形式不做假定，由历史信息直接去确定验前分布采用经验贝叶斯方法［2］

由上式可以看出，f(x)中包含了π(θ)的信息，因此，子样X中应含有验前密度的信息。从上式中解出 π(θ)，那么，π(θ)就是f(x)和p(x|θ)的函数。p(x|θ)实际上就是经典统计中的似然函数，当总体分布为已知时，它可以计算出来，而当验前样本容量足够大时，也可以运用非参数方法确定出密度的估计。

3.1.3 如果要求验后分布的计算方便应采用共轭方法

运用共轭验前分布有个突出的优点就是验后分布的计算方便。表1给出了几种常用的共轭验前分布。

表1 常用共轭验前分布

验后分布的一些参数可以得到很好解释。例如，正态均值（σ方差已知）的共轭验前分布是N(μ，τ2)（这里μ，τ已知），其验后均值为

3.1.4 凭借经验的“主观概率”方法

这种方法最典型的是所谓的“专家打分”法［3］。假定θ为未知分布参数，则将θ的取值范围分成K+1个档次。然后请n个武器装备系统专家填写θ属于的档次，并将专家的意见总结归纳。如表2所示。

表2 专家打分表

表中n1+n2+...+nk+1=n，由此可以做出θ的频率图，用函数逼近的方法确定出θ的近似验前分布函数。

确定验前分布的统计方法还有许多种，如最大熵方法、随机加权法［4］确定先验分布，由子系统信息确定先验分布等，武器装备系统试验中具体使用哪一种方法要根据实际情况而定。

3.2 验前信息的相容性检验

武器装备系统试验能够应用验前信息的前提是验前信息能够反映未知参数的统计特征，即验前信息与现场试验信息应该服从同一总体，否则系统试验得出的结论是不可信的，这就是验前信息与现场信息的相容性问题。本文针对武器装备系统验前信息和现场信息的不同情况，研究了两种相容性检验方法，在一定的置信水平下，判断两个子样的相容性。

总之，东北化肥冬储的大幕早已启动，只是由于市场供给发生了变化，冬储的形式与节奏也在发生改变。基础化肥继续上涨的动力不足，后市以窄幅波动为主。

3.2.1 参数检验法

在武器装备系统试验中，如果某未知参数总体分布的类型已经确定，则适用参数方法进行相容性检验［5］。对参数的假设检验，针对不同分布的参数和同一分布不同的参数，都要构成不同的检验统计量，本文研究了贝叶斯置信区间估计方法。

假设确定了作战系统中某未知参数θ的分布类型后，结合验前信息确定θ的验前分布为π(θ)，这样就可以得到显著性检验的贝叶斯验前置信区间（显著性水平记作α）为（θ1，θ2）。其中θ1，θ2由下式确定：

取得损失函数和无信息验前分布，则可由现场信息得到未知参数θ的贝叶斯估计值为，如果落在(θ1，θ2)内，则认为两总体无显著性差异，即验前、验后数据对于未知参数θ是相容的。否则，该验前信息不能使用，或只有通过折合后才能使用。

3.2.2 非参数检验方法

对于武器装备系统各种分布类型的历史数据或仿真数据，非参数检验方法［6］通常使用更为简便。本文根据系统需求主要研究了秩和检验方法。

设样本(x1·，xm)和 (x′1，x′2，·，x′n)分别是来自总体X和X′的观测值，其中m和n都大于1，假定m＜n，现要求检验统计假设H0：X和X′为同一总体。

将两个样本混合，并由小到大重新排序，构成顺序统计量：

若xk=zj，则记rk(x)=j，称为xk在混和样本中的秩，在实际中可能会出现部分观测值相等的情况，对这些观测值的秩定义为在混合样本中下标之和的平均值，例如若xk=zj=zj+1，则rk(x)=(j+j+1)/2=j+0.5。于是定义样本(x1，·，xm)在混合样本中的秩如下［7］：

上式中T为检验统计量，如果两组数据相容则T不宜过大或过小，给定显著性水平α，设此检验的接受域为(T1，T2)，则有检验准则：

当T满足上式中不等式时接受H0，即X和X′为同一总体，反之拒绝［8］。

武器装备系统各种各样的验前信息经过确定其分布类型、及相容性检验就完成了验前信息的预处理。

4 计算应用实例

某型雷达在单机试验时积累了一定的数据。本文就该型雷达的威力指标进行研究。求出该型待试雷达最大作用距离的历史数据，共六组G（y）如下：86.623 86.827 85.419 80.043 81.237 87.054 88.112，作为验前信息。已知在系统试验时雷达经过10个有效航次的外场试验，该待试雷达实际对某型目标的最大作用距离数据F（x）如下：F（x）=［82.543 84.713 84.209 85.523 85.918 83.926 83.389 86.765 84.478 85.333 83.459 83.776］。

两组数据如表3所示。

表3 F（x）和G（y）两组样本

下面判断现场数据F（x）和验前数据G（y）是否为同一总体。

检验假设H0：F（x）=G（y）（取α=0.05）［9～11］

将两组样本合在一起由小到大排列，统一编号，并计算出相应的秩，列于表4。

表4 样本求秩

其中yi一组容量较小，统计量T=1+2+10+13+15+16=57 对于检验水平α=0.05，n1=6，n2=10查秩和检验表得T1=33，T2=69，由于

T1＜T＜T2即：P(T1＜T＜T2|H0)=1-α

故接受H0，认为F（x）和G（y）无显著差异为同一总体。否则认为F（x）和G（y）存在显著差异并非属于同一总体。

通过相容性检验的F（x）和G（y）两组数据可采用共轭方法得到验后分布参数为μ1=84.5811，σ1=0.1462。

分析引入验前信息之下的Bayes估计与传统估值方法比较带来的益处。当不运用验前信息时，传统的方法取作为Rmax均值的估值，此时

对于利用验前信息时，设有m个验前最大作用距离信息，验后距离数据有n个［12］，则

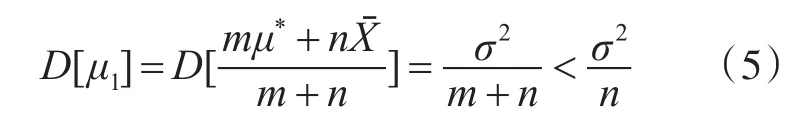
因此通过利用验前信息获得的最大作用距离的均值有较高的精确度。

5 结语

在武器装备试验样本量越来越少的今天，验前信息已经成为重要的试验资源。验前信息的充分利用可以提高试验结果置信度。本文就如何科学合理地利用不同种类的验前信息进行分析，确定了包括信息分布形式，及进行相容性检验的验前信息预处理过程，并通过实例验证了该方法的科学合理性，对于今后的武器装备试验中验前信息的应用及试验结果综合评定具有一定的价值。