基于响应面法的船用柴油机燃油消耗率与排放性能分析*

2019-07-08

舰船电子工程 2019年6期

（西安航空职业技术学院西安 710089）

1 引言

根据我国地理环境资料统计数据可知，海拔高度达到1000 m以上的区域面积在国内的总面积占比为56%，其中有32%面积属于海拔达到2000 m以上的高原地区。在这些高海拔地区运行着许多由内燃机提供动力的商用船、乘用船、农业工程设备等。由于高原地区普遍存在大气环境压力偏低的现象，这对柴油机的正常运行造成较大危害，具体表现为动力不足、污染物气体含量上升、运行状态恶化、稳定性变差等［1～5］。为克服上述问题，我国针对在高源地区使用的内燃机制定了相应的国家标准［6］，明确规定了普通增压、自然吸气与高原动力机械各自合理的的海拔高度范围，同时设定了各个海拔条件下动力机械保持正常运行状态的下限参数。对柴油机的排放指标进行控制的最关键部分是要实现颗粒物（PM）与氮氧化物（NOx）含量的同时降低，为克服上述难点，可以采用排气再循环（EGR）方法以及可变截面涡轮增压工艺进行改善。考虑到EGR系统是利用EGR回路来实现进气管和排气管的连通，同时在可变喷嘴涡轮增压器（VNT）和进排气歧管之间也通过物理结构进行连接，而且排气再循环流量以及涡轮叶片都通过排气能量进行驱动，这二个系统间具有明显的耦合作用［9］。所以，必须深入探讨以上三种情况对柴油机的运行成本、动力性与排放性造成的影响，从而显著改善高原地区的柴油机运行性能，同时也可以为各海拔条件下匹配EGR和VNT系统的柴油机提供控制参考标准。

2 试验

2.1 试验设备

本实验选择一台采用增压中冷方式以及具有直列4缸4气门的船用高速直喷柴油机作为测试对象，同时为该机配置了VNT和高压EGR控制系统，从表1中可以看到各项技术参数。测试时需要使用的仪器有功率测试机、气压模拟设备、监测设备、机油恒温调控设备、燃油恒温控制装置、循环水保温系统、排放尾气测试系统、自动标定系统等。表2显示了进行台架试验时需要使用的各个仪器，从图1中可以看到台架的具体布置结构。

考虑到测试区域海拔高度基本都在1950m左右，气压约80kPa，所以在大气模拟装置中测试了柴油机运行性能与大气压力之间的变化关系。测试地区的气压高低会对柴油机进气、排气的压力产生明显影响，如果需要模拟比当地大气压力更大的气压时，可通过对进气和排气实施加压的方法来完成；如果需要模拟比当地气压更低的大气压力，可以通过对进气进行节流和降低排气引射的方式来完成。本研究选择ToCeiL-KT2400发动机进气空调来加压处理柴油机的进气端，在排气端将背压阀控制在不同的开度来模拟得到大气压分别等于90kPa和100kPa时对应的环境出口压力。

表1 试验用发动机基本设计参数

表2 主要测试设备的特性参数

图1 台架布置示意图

2.2 响应面法

可以利用响应面法（RSM）来统计分析多变量问题，具体方式为先选择合适的试验方法测试获得一组数据，再通过多元二次回归方程拟合得到响应和因子的函数变化关系，构建得到由连续变量组成的曲面模型，再评价因子之间的交互作用。考虑到EGR、VNT以及大气压力之间会发生相互作用，因此可以采用响应曲面分析方法来处理各个因子交互作用。此时，应在典型工况下运行，对应的最大转矩转速为2200r/min，额定功率转速为4000r/min，根据响应面法来完成曲面图形式的响应过程，研究VNT喷嘴环的开度、大气压力与EGR阀各参数间的交互作用所引起的船用柴油机运行性能和排放情况改变。

3 结果分析

3.1 模型建立

Box-Beknken设计是一种适合对因子数介于3～7个之间的情况进行响应曲面设计的方法，该方法只需很少的试验次数便可以高效完成设计过程，而且不会发生各个因子都同时达到高水平的情况。对于设定的二个典型工况，依次确定VNT喷嘴环开度、大气压与EGR阀开度各因子的合理取值，利用Box-Behnken设计方法完成试验设计与建模过程并研究柴油机响应参数受到各因子交互作用的影响。从表3中可以看到实际测试结果和编码水平数据，可以采用如下公式对两者进行转换：

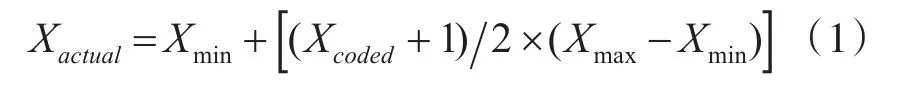
上式Xmin是因子最小值；Xactual是因子实际值；Xmax是因子最大值；Xcoded是因子编码。

表3 编码水平表

本文选择Minitab软件并通过Box-Behnken设计方法根据表3给出的因子水平，测试了动力性参数的转矩，分析了燃油消耗率并以烟度和NOx比排放作为响应参数，依次对两种典型工况开展测试。同时为降低测试误差并获得更高的模型拟合精度，对各工况都进行了2次仿行，在每种工况下都实施了30次测试，包括24个析因点以及6个区域中心点。

通常情况下，利用二阶模型已经能够满足对大部分发动机系统进行设计时的真实响应曲面要求。所以，需结合测试设计矩阵的各行因子组合方式开展试验过程，并做好响应参数记录，采用逐步回归法来完成因子和响应关系的二阶多项式拟合，由此获得两种工况条件下每个响应以因子实际值为依据的回归模型。

当运行工况为2200r/min的全负荷状态时，每个响应对应的二阶回归模型见式（2）～（5）：

当运行工况为4000r/min的全负荷状态时，所有响应对应的二阶回归模型见式（6）～（9）：

3.2 结果评价

可以通过对比p值和显著水平来判断响应模型是否能够实现对数据的准确拟合。其中，最优状态是显著性水平等于0.05，此时代表模型和数据无法拟合的概率只有5%。从表4中可以看到对响应模型进行方差分析得到的p值，可以发现，所有模型p值都在0.001以下，由此可以推断所有二阶响应模型都满足显著性条件。

为保证模型能够满足准确性与适应性要求，还应准确评估模型预测能力，通常使根据回归模型显著性测试结果进行判断，同时选择决定系数R2和调整决定系数R2 adj对模型逼近程度进行分析，并利用预测决定系数R2 pred分析回归模型预测性能。通常而言，当一个模型精度符合要求时，R2 pred值介于0.8～0.9之间，同时，R2 pred和R2差值应在0.2～0.3以内。表4给出了对各个响应曲面模型进行评估所得的结果。可以发现，R2、R2 adj、R2 pred值都高于0.91，同时R2 pred和R2差值都在0.2以内，由此可见所有响应曲面模型都能获得一致的测试结果并达到相同的预测能力。