基于比例故障模型的发射车液压系统状态维修决策*

韩 华 余仁波 柳洪刚

（1.海军潜艇学院 青岛 266000）（2.海军航空大学 烟台 264001）

1 引言

液压系统是导弹发射车的重要组成部分，主要完成导弹发射车的调平和起落架的起竖工作［1］。液压系统工作负载大、环境复杂，容易出现爬行、渗漏等故障。实际上，如果液压系统设计制造质量好，则造成故障的原因大多是维护及保养不当引起的。液压系统70%的故障发生率，与液压油有关，在这70%中约有90%是由于杂质破坏所致［2］，所以液压系统服役期限的长短取决于液压介质的清洁度以及液压系统运行中的正确监测、维护及保养。

状态维修（Condition Based Maintenance，CBM）作为一种新的维修思想，考虑系统运行的状态、系统个体差异，尽可能在故障发生前进行维修，降低故障发生概率，减少维修费用、提高装备使用可靠度、提高装备的利用率［3～5］。在状态维修中，建立CBM模型的目的就是在系统运行过程参数与系统本身完好程度之间建立精确的联系［6］，它可分为确定性模型和概率性模型两种，建模方法大致包括基于概率统计理论的方法和基于随机过程理论的方法两大类。针对液压系统状态监测数据复杂、稳定性差的特点，利用威布尔比例故障率模型能够处理多个因素对生存时间影响的问题，又能在计算故障率的同时考虑寿命和状态信息的优势，建立比例故障率模型。在保证最大可用度下，利用模拟的液压系统监测数据对维修决策方法进行了仿真，得到具体的维修决策方案。

2 比例故障模型

比例故障率模型（Proportional Hazards Model，PHM）又称Cox模型［7］，是一种适用性很强的寿命数据统计分析方法，属于一种根据装备状态监测和历史寿命等数据信息建立某一装备失效模型的建模方法。该模型的最大优势是能够处理多个因素对生存时间影响的问题，又能在计算故障率时同时考虑寿命和状态信息，有着其他模型无法比拟的优点。

比例故障率模型是指这样一类模型，其模型具有如下性质：不同个体的故障率函数成比例。PHM中引入新的信息，称为协变量，反映装备伏态信息，如振动或油料分析测量的数据。比例故障率模型的基本形式为

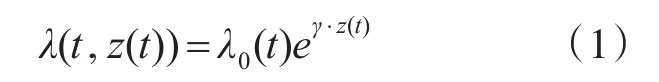
其中：λ(t，z(t))为故障率；z(t)为协变量，即运行状态的监测值，也可以是任何反映系统状态的因素；λ0(t)为仅与时间相关的基本故障率；回归参数γ表示协变量对故障率函数的影响。

从式（1）可以看出，对于两个同类系统分别给定协变量值，其故障率函数之比为

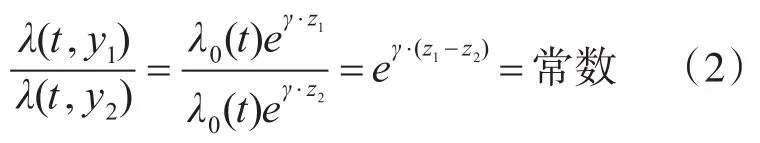
因此，两个系统故障率函数之比不随时间t的变化而变化。

2.1 模型假设和符号说明

1）模型假设

（1）故障率函数的比值不依赖于时间t；

（2）完全信息水平，即在监测时，获得的关于系统状态的信息是完全的；

（3）在状态数据使用方面只使用状态监测数据，不考虑事件数据，例如，装备安装、停工、大修等；

（4）只考虑单系统状态。

2）符号说明

β、η是模型中待估计参数，β为形状参数，η为尺寸参数；γ是p维协变量γ=[γ1，γ2，…，γp]的回归系数矢量；z是p维协变量z=[z1，z2，…，zp]的系统状态监测特征量矢量；R(t)为可靠度函数；f(t)为样本分布的密度函数；λ(t)为故障率函数；n为n个试验样品；i为试验样品的编号，如第i个试验样品；δi为0-1变量，δi=1表示第i个样品在试验过程中发生了故障，δi=0表示第i个样品在试验过程中没发生故障；Ai为第i个试验样品的剩余寿命。

2.2 威布尔比例故障率模型WPHM

威布尔分布是可靠性工程领域中应用最为广泛的寿命分布［8］，其最大优点在于对各种类型的试验数据具有极强的适应能力。两参数的威布尔分布的基本形式为

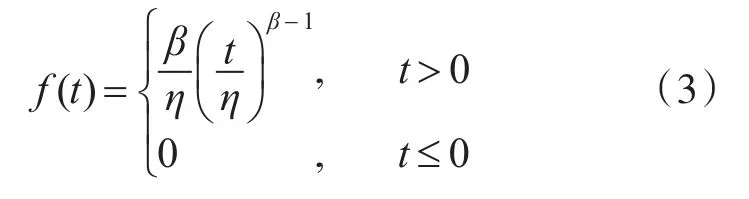
从式（5）可以看出δi是一个示性变量，δi=1表示第i个样品在试验过程中发生了故障，则Ti=Ai；δi=0表示第i个样品在试验过程中没发生故障，则Ti=Li。这时，n个样本的似然函数为

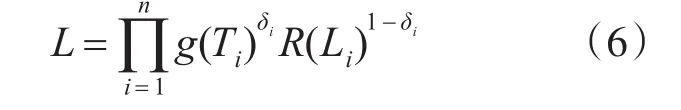
其中，β、η为参数。

下面介绍建立威布尔分布比例故障率模型的过程。

1）样本数据的建立

比例故障率模型能够很好地建立起系统运行状态和故障率之间的关系，对各种类型试验数据具有极强的适应性，能够在考虑系统内部状态的同时也考虑到运行环境、负载大小以及系统运行历史数据等因素对装备寿命的影响。因此在建立该模型的开始阶段，要尽可能全面地考虑所有影响系统运行寿命的因素，通常将各种状态信息特征量和环境应力、工况条件等均作为伴随变量考虑进来。

2）涉及截尾的问题

寿命数据的一个重要特点是广泛存在截尾现象。截尾数据的样本分布与通常数据的分布是不同的，截尾的机制不同，在建立模型时也必须考虑找到不同的参数估计和校验方法。

假定考察n个样本，分别规定试验截尾时间L1，L2，…，Ln，第i个样品的寿命为Ai，假定各样本寿命分布为独立同分布的，其密度函数为g(t)，可靠度函数为R(t)，样品i的寿命Ai只有在Ai≤Li时才能被观察到。在此条件下，试验后可得到第i个样品的工作时间长度Ti，其表达式为

引入0～1变量δi表达式为

如果在n个样本中有r个发生故障，可以在实验结束后对样本进行重新排序，将故障样本排序为第1到第r，第r+1到第n个样本为截尾样本。这时，样本的似然函数为

3）伴随变量的筛选

状态监测数据在可靠性理论中普遍定义为协变量，在对比例故障率模型进行建模时，协变量可以分为外部协变量和内部协变量。外部协变量是影响装备的外部环境因素，一般不会随着系统运行过程而发生改变，进而不会引起系统风险特性的变化。而内部协变量是装备内部随机过程产生的输出，随着系统的运行而发生改变。

设计协变量的相关系数矩阵，为了使各个伴随变量参数之间独立性较好，要求各变量之间的偏相关系数尽量小，可以用主成分分析、聚类分析、因子分析等降维方法来从相关的参数里选择出相互独立的变量参数。

在变量筛选过程中，通常显著性水平P值在置信度为95%下，小于0.05的变量被纳入模型，大于0.1的变量则从该模型中剔除。

同时必须注意，经过筛选后的伴随变量要与实际情况相吻合，尽可能使选择的参数能较为完整地从多个方面反映系统或者装备的失效状态。

4）WPHM模型的建立

协变量筛选得出之后，比例故障率模型中的基准分布函数决定该模型的类别，威布尔分布是可靠度理论及有关寿命等问题中常采用的分布之一，比例故障率模型中基本故障率函数为威布尔分布时［9］，令

然后，将式（3）代入式（1），得到威布尔比例故障率模型为

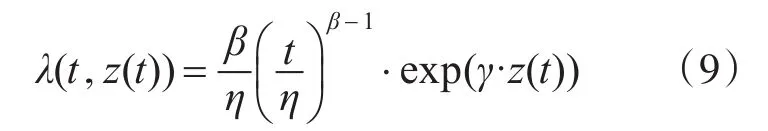
式中，γ为p维协变量γ=[γ1，γ2，…，γp]的回归系数矢量，z为p维协变量z=[z1，z2，…，zp]的系统状态监测特征量矢量。

WPHM模型中待估计的参数有β，η，γ，常选择极大似然估计法对其进行参数估计。

5）WPHM模型的参数估计

在应用比例故障率模型之前，需要先对模型中的参数β、η、γ进行可靠性估计，从而确定模型的具体形式。矩估计法、图参数估计法和极大似然估计法是常见的可靠性参数估计方法。极大似然估计法在处理截尾数据的情况下具有明显的优势，所以，利用极大似然估计法对威布尔比例故障率模型中的参数进行估计。

由f(t)=R(t)λ(t)，对式（6）进行变换，得到：

令λ0(t)=f(t)，将式（3）代入式（10），得到似然函数：

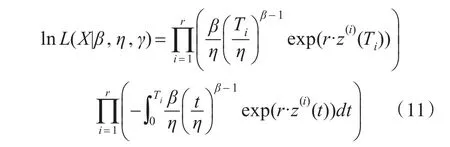
对上式取对数，得到lnL为

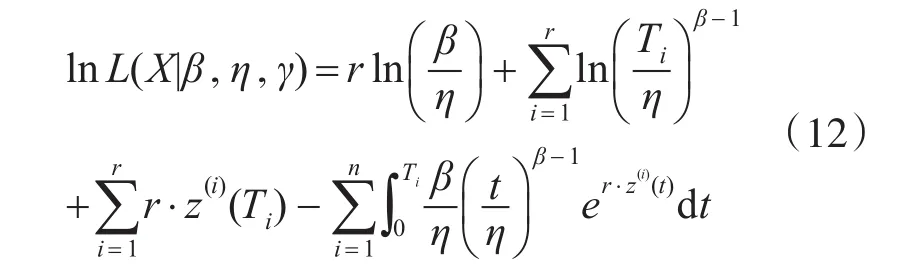
根据极大似然估计法，分别对对数似然函数lnL(X|β，η，γ)中的待估计参数β，η，γ求偏导数，令各偏导数等于零得到非线性方程组。将监测得到的协变量zi(t)及寿命数据t代入方程组，用New-ton迭代法或者Nelder-mead's算法可以求解得到β，η，γ的估计值，，，从而得到参数估计后的威布尔比例故障率模型为

当确定了状态与故障率函数之间的关系后，按照一定的目标函数（最小维修费用或者最大可用度等）建立维修决策模型，以故障率作为决策变量就可以得到故障率的阈值，最后根据状态计算出当前故障率分布，与阈值比较选择合适的维修措施。

3 以最大可用度为目标函数的维修决策

假设装备在一个预防维修周期内，平均工作时间为Tu，平均维修时间为Td，平均预防性维修时间为Tp，平均修复性维修时间为Tc（Tc＞Tp），因此，每一次预防性维修周期维修时间Td为［10］

其中，R(T，Z)是系统在T时刻的可靠度，得到一个预防性维修周期内装备平均工作时间的Tu，即

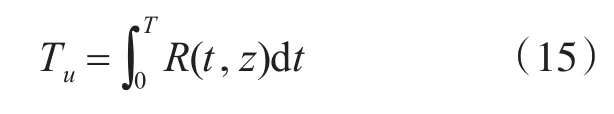
进而，得到稳态可用度［11］为

显然，当θ最小时，A最大，所以下面求得最小的θ。

由于已经根据历史数据回归出了装备故障率与时间和伴随变量的关系，并且稳态可用度只有一个极值点。因此，可以用数值解法算出其中一组失效数据的平均可用度最大时的更换间隔期T，将此最佳更换维修时间T和T时刻对应的伴随变量值代入回归的故障率模型，得到一个故障率λ′，然后以此为标准就可以对相同型号的装备实测数据进行决策。

要使新装备的平均可用度最大，其故障率λ必须小于故障率阈值，换句话说就是如果λ大于等于λ′就必须维修，即

其中，β、γ、η为比例故障率模型中的参数，然后，将式（19）两边取对数，得到

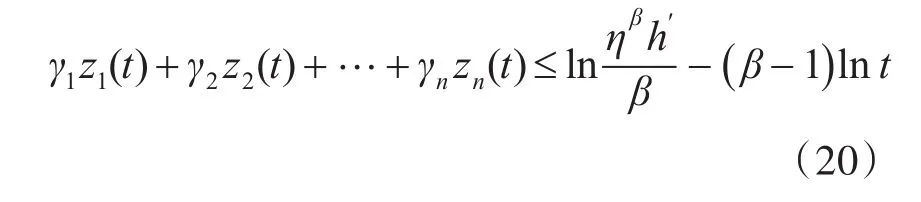
式中，n为状态监测次数，zn(t)表示第n次监测时系统的状态信息。

以式（20）作为维修决策判别式，将监测的状态参数z1(t)、z2(t)、…、zn(t)和时间t代入式（20）进行计算，如果此式成立，则继续工作；否则，需要进行预防性维修。同时，如果运行过程中出现故障，则立即进行维修，维修后系统如新，状态恢复到初始状态。

4 基于最大可用度的比例故障率模型仿真

从状态数据中截取20组故障状态的数据作为样本数据，以液压系统故障时状态评估数据［12］为自变量，监测的调平油缸压力、分流集流阀流量、……、齿轮泵温度、液控单向阀压力、主管路压力等16个参数为预设协变量。

当存在多个协变量对状态评估值均有影响时，首先需要通过相关性分析确定显著性协变量，然后建立协变量与状态数据之间的关系模型，并根据该模型中协变量的作用大小，对当前液压系统的状态进行分析和预测。各协变量的计算结果见表1。

同时，得到显著性分析的残差分布如图1所示。

然后，根据表1的分析结果，按照P值检验准则，可知水平变送器压力、滤油器流量、齿轮泵温度、液控单向阀压力、辅助泵出口压力、手摇泵出口压力、泵出口流量八个协变量因无显著作用而被剔除，最终余下八个协变量分流集流阀流量、调平油缸压力、起竖油缸位移、泵出口流量1、锁定油缸压力、分流节阀流量、换向阀压力、主管路压力被筛选进入模型，记为

另一方面，由图1显著性分析残差分布结果可知，预测值与观测值的分布类似，且回归方程预测值与已观测值的标准残差分布集中，说明回归方程的预测效果比较好，即选择的八个显著性协变量能够解释大部分的协变量。

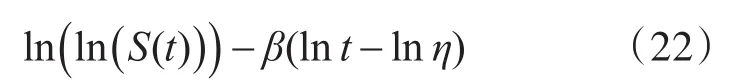
即lnt与ln(l n(S(t)))或ln(H(t))之间呈线性关系，按照装备使用经验［13］设定C1C2为0.012，根据历史故障数据，联立式（13）、式（21）和式（22），利用Matlab编程，采用最小二乘优化方法，解出联立的超定方程组，有

式中，X(t)={x1(t)，x2(t)，…，x8(t)} 分别表示分流集流阀流量、调平油缸压力、起竖油缸位移、泵出口流量1、锁定油缸压力、分流节流阀流量、换向阀压力、主管路压力的状态监测数据。

以最大可用度为目标进行决策，由式（15）设定故障维修时间与预防性维修时间之比：

其中，Mct为故障后维修时间；Mpt为预防性维修时间。由式（16）、式（23）和式（24）得到系统可用度曲线如图2所示。

分析图2系统可用度曲线，可知：

1）系统在刚开始运行时，即时间小于6000h时，系统的可用度增加明显，实际上系统刚开始运行存在磨合期，这时可靠度相对较低，随着系统磨合的进一步深入，系统的稳定性和可靠性都在显著增加；

图2 系统可用度曲线

2）系统在运行6234h后可用度达到极大值0.961，这时系统磨合成熟，可靠度高，运行稳定；

3）当运行时间大于6300h，系统可靠度在慢慢下降，但是下降的幅度远比磨合期增加的幅度要小，系统运行比较可靠。

由图2得到系统运行到最大可用度0.961时的时间t=6234h，将t以及t时刻的状态数据代入式（23）得到维修的故障率阈值λ′=0.003，根据式（19）做出维修决策曲线，将当前时刻监控到的状态参数代入式（23）计算，并在图中画点。该点若处于决策曲线上方，则立即维修；若处于曲线下方，则继续工作。根据仿真状态数据，代入式（23）得到决策值，并在图中画出决策点如图3所示。

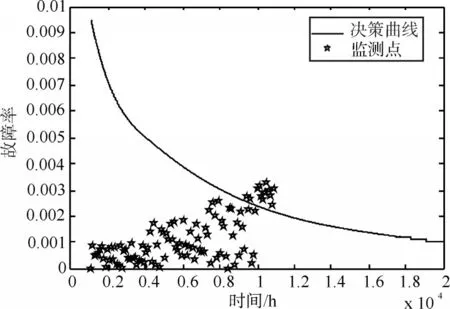
图3 故障维修决策图

分析图3故障维修决策图，有以下结论：

1）系统的故障率呈现逐渐增加的趋势，并且在系统磨合期结束时可靠度最大，即可靠度最大的时故障率最低，这与实际情况是吻合的；

2）系统在运行一段时间（自然时间）后，即在9000h后开始出现故障，分别在9101h、9235h、9488h、9625h、9941h、10148h、10308h、10571h、10728h、10963h、11035h、11605h出现的故障需要立即维修，共计12次。

5 结语

针对液压系统状态监测数据复杂、稳定性差的特点，采用威布尔比例故障率模型处理多个因素对生存时间影响的问题，通过相关性分析确定显著性协变量，建立协变量与状态数据之间的关系模型，并根据该模型中协变量的作用大小，以最大可用度为目标，综合考虑寿命与状态信息，采用模拟监测数据对维修决策方法进行仿真。仿真结果表明，比率故障率模型仿真决策方法注重对故障信息的分析，可得到装备故障率阈值，液压系统维修决策科学、合理。