基于贝塞尔大地反解问题的靶船航向角计算方法*
2019-07-08
(92941部队 葫芦岛 125000)
1 引言
任务中实时计算脱靶量是通过估算的导弹中靶时刻位置和实测的靶船中心点位置和航向,求解导弹在靶船测量坐标系下的相对位置偏差——即实时脱靶量数据[1]场,靶船位置有两个数据来源:数据源一是靶载设备的GPS1测量系统接收并记录导航卫星信息,与基准站信息进行伪距或载波相位差分处理,获得WGS-84坐标系下的靶船定位参数;数据源二是GPS2测量系统接收的主靶船位置、航向及状态信息。当遇到大气的扰动及接收机附近的干扰影响的时候,可能会收不到船载GPS2系统的航向角信息。脱靶量计算在将落点从地心坐标系转换到靶船坐标系的过程中,航向角是必要条件之一。本文讨论在未收到航向角的时刻,如何结合接收到的两套靶载装备GPS测量系统的数据来估算航向角补全条件进行脱靶量计算。
2 基于贝塞尔大地主题方算方法求解航向角
算法思想:靶船航向角是船的艏艉连线与真北的夹角α,顺时针方向为正。如图1所示,设在WGS-84坐标系下,GPS1测量系统的地心坐标为(X1,Y1,Z1),GPS2 测量系统的地心坐标为(X2,Y2,Z2),两者连线为l,为了计算方便和直观,我们把l平移至l′,使其过靶船中心,得到l′与真北的夹角β。
第一步,由两个GPS测量站的大地坐标求解测站连线的方位角。由图1可以看出,两个GPS测量天线的连线l与真北的夹角,也就是l′与真北的夹角β。
在众多求解大地线距离及大地方位角的算法中,较为常用的算法模型有贝塞尔大地主题解算方法。贝塞尔算法是将椭球面上的大地元素按照贝塞尔投影条件,投影到辅助球面上,在球面上进行大地主题解算,再将球面上的计算结果换算到椭球面上。如图2,椭球面极三角形NOQ投影到球面三角形N′O′Q′,其中,椭球面三角形中N为极点,O(L1,B1)Q(L2,B2),OQ的大地方位角为A12,球面三角形中N′为极点的投影,O′(λ1,φ1),Q′(λ2,φ2),O′Q′的大地方位角为α1。

图1 航向角示意图
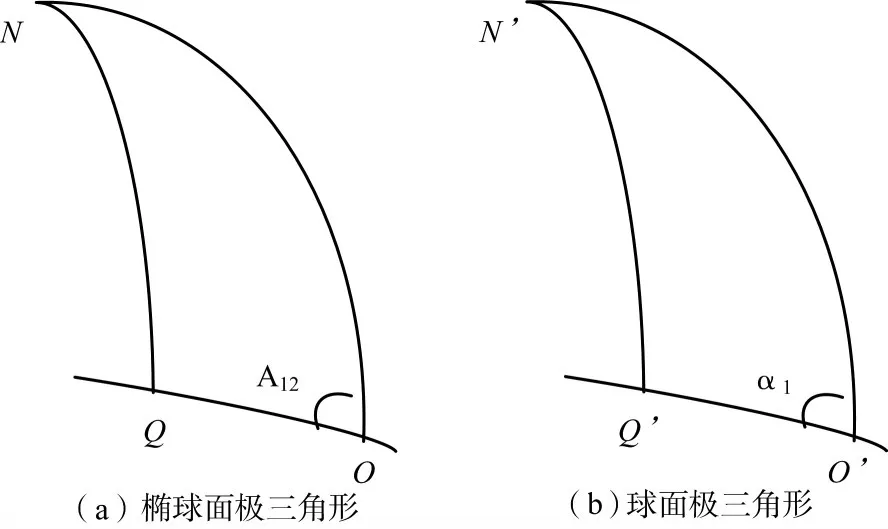
图2 贝塞尔投影图
根据球面和椭球面上坐标关系,在贝塞尔投影条件下,方位角投影保持不变,即A12=α1。
为计算OQ的大地方位角A12,要用到的球面三角形中的三角函数间的基本公式主要有:

其中,Δλ=λ1-λ2为两点经度差,σ为 球面上两点间大圆弧长。
为确定方位角α1,式(1)除以式(2),得

根据以上的投影坐标关系可得到


到这,根据贝塞尔大地主题解法,就可以求得靶船上GPS测站1到GPS测站2的方位角,也就是图1中的l′与真北的夹角β。
第二步,求l与艏艉线的夹角γ。在通过测量靶船GPS2测量系统GPS天线和GPS1测量系统GPS天线的安装位置距靶船中心的偏移,得到两套测量系统GPS天线在靶船坐标系的坐标分别为(dx1,dy1),(dx2,dy2)。如图3所示。

图3 GPS天线安装位置示意图
则:

第三步,则通过大地方位角β,与两个GPS测站的连线与艏艉线的夹角ɤ之间作差,求得航向角

3 实例分析
在XXX任务中,靶载设备的GPS1测量系统和GPS1测量系统对靶船位置实时定位,通过上述基于基线矢量的方法计算航向角,完成了实时脱靶量的计算,与实际检靶结果相比,精度高,误差小。

信息来源 脱靶量误差信息来源GPS1测量系统GPS2测量系统推算的航向角159.8实时脱靶量结果x 11.78 10.42 z x z 8.17 12.26 3.97 2.61 4.17 1.26
4 结语
本文针对海上靶场沿海环境复杂,靶载设备信息传输不稳定,中心计算机接收船载定位数据不连续的问题,充分利用中心计算机接收来自靶船的两套GPS测量系统的有利条件,研究了基于基线矢量的计算船体姿态角的方法的靶船定位补偿措施,估算出高精度的靶船定位结果,为准确计算脱靶量提供可靠数据源。
