地理加权回归模型的城市住宅价格多源热度分析

江济强，王斌，王明建，杨毅

(1.广东省国土资源测绘院，广东 广州 510500； 2.淮海工学院测绘与海洋信息学院，江苏 连云港 222005)

1 引 言

住宅价格问题是目前社会讨论的焦点之一，研究城市区域间住宅价格分布差异很有必要。而城市不同地区住宅价格一般是分区域聚集的，说明城市住宅价格分布差异是有规律的[1]，具体来讲，就是距离学校、医院、公园、购物中心等地的距离决定了对住宅价格影响的大小[2]。随着地理信息、互联网等技术的进步，越来越多的分析方法相继涌现。陈震[3]收集昆明城市各小区住宅价格，用GIS进行数据分析建模，结果表明，昆明城市住宅价格由中心向四周递减，教育、交通、容积率等因素作为次要因素影响着住宅价格。张媛[4]通过报刊等媒介收集银川市商品房数据，综合GIS分析城市的交通、环境、教育、结构等都是影响城市住宅价格的因素。熊海璐，吴晓燕等[5]通过最小二乘法分析武汉住宅价格表明住宅周围的环境和位置是决定住宅价格的最重要因素。

对于未来住宅价格的预测分析以及规律寻找，最合适的方法就是借助互联网大数据建立回归预测模型来进行分析预测。陈向阳、陈日新等[6]利用多元线性模型研究2003年～2010年广州市住宅小区价格分布趋势，发现广州市住宅小区价格由市中心CBD向四周呈递减趋势，一线城市离CBD的距离是影响住宅价格的主要因素。付益松[7]通过构建南昌市2015年3月～10月的住宅价格数据库，利用GIS克里格插值法进行分析得出影响住宅价格因子的重用大小依次为：区位、交通、公共设施、环境。

多元线性回归模型和最小二乘法模型参数与位置弱相关，预测的精确性和可靠性较难满足分析需求，地理加权回归模型由于其在某些非平稳性问题研究上具有上述模型所没有的优势[8]，近年来得到较快发展。本文提出一种地理加权回归模型算法，通过互联网采集研究区内住宅小区价格及绿化率、购物中心、公园、中小学、大学、医院等分布数据，并纳入该模型中，全面分析住宅价格受绿化、交通、学校、医院、公园等影响大小，揭示小区住宅价格的空间分异和不同因子的相关系数。

2 地理加权回归模型(GWR)

多元线性回归模型是用描述多个变量对一个变量产生影响的计算模型，一般难以处理变量数据实时改变的情况，主要在系统事故数值研究，系统故障提供预测以及用于海洋各成分元素研究[8]。为有效分析空间多个平稳性变量之间相互影响关系，并且有效消除非平稳性所带来的误差，本文采用地理加权回归计算模型(Geographically weighted regression，GWR)，表达式为：

(1)

其中，(ui，vi)为第i个样本点的坐标，βk(ui，vi)为第i个样本点的第k个回归系数，εi为第i个样本点的随机误差，服从数学期望为0，方程为σ2的正态分布。不同样本点i和j的随机误差相互独立，协方差为0。即满足：

εi∝N(0，σ2)；Cov(εi，εj)=0(i≠j)

按照加权最小二乘准则对式(1)进行最优估计，建立目标函数表达式为：

(2)

其中，wij为第i个样本点与样本点j之间的核函数，与距离dij相关。

(3)

(4)

利用地理加权回归模型做出的住宅价格分析，有效考虑了影响住宅价格的众多要素，消除了非平稳性因素的影响，若将式(1)中，βk(ui，vi)=βk(uj，vj)(i，j=1，2…n)，回归系数不随空间位置变化而变化，则退化为多元线性回归模型，两种模型比较如表1所示。

两者模型比较 表1

3 GWR模型多源热度分析

通过互联网手工及自动抓取研究区住宅价格并记录小区位置及均价，将绿化率、公园、小学等学区以及医院、购物中心等纳入主要影响因素，分析该区住宅价格高低区位变化。通过建立特征价格模型，把影响因素分为内部因素、外部因素两大类别，内部因素研究直接可以进行建模分析，外部因素通过坐标计算距离，通过距离间的关系来研究。

Yi Yang等指出外部因素对住宅价格影响范围研究在 1.5 km内结果最佳[8]。按照小区 1.5 km范围内小学、中学、大学、医院、公园、购物中心个数为依据来研究各因素对住宅价格影响大小。采集了该辖区124个小区的住宅价格和其他自变量的坐标数据，并将变量统一取对数值，如表2所示(部分数据)：

住宅销售特征价格变量计算方法和说明 表2

3.1 数据预处理

(1)坐标转换

由于互联网地图抓取的点经纬度为球坐标，为计算小区与各因子的距离，需把球坐标转换成平面坐标，本文利用ArcGIS软件进行坐标转换，如表3所示(部分数据)：

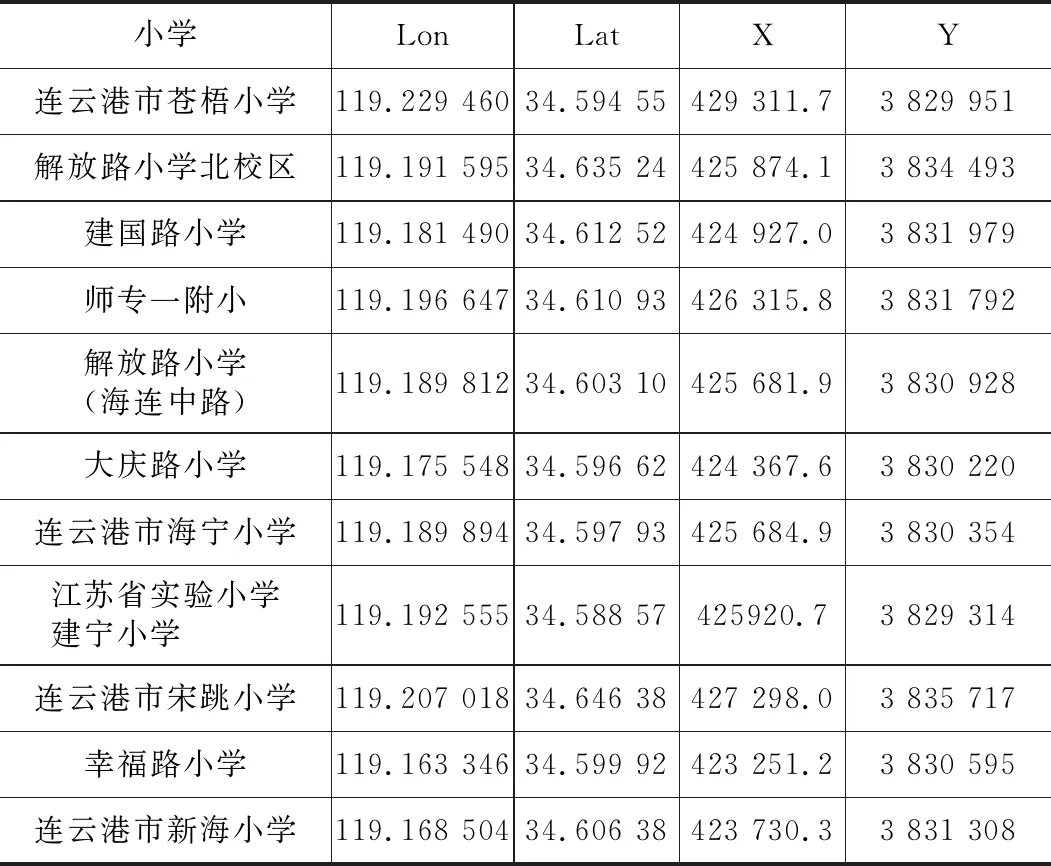
小学球面坐标转换为平面坐标表 表3

(2)计算变量

统计小区1.5 km范围内绿化率、小学、中学、大学、公园、医院、购物中心数量，对各变量取ln值，如表4所示(部分数据)：

变量分布表 表4

续表4

3.2 各因子热度分析

利用式(3)、式(4)，结合互联网采集预处理后成果，对各影响因素进行计算并输出制图，如表5及图1所示：

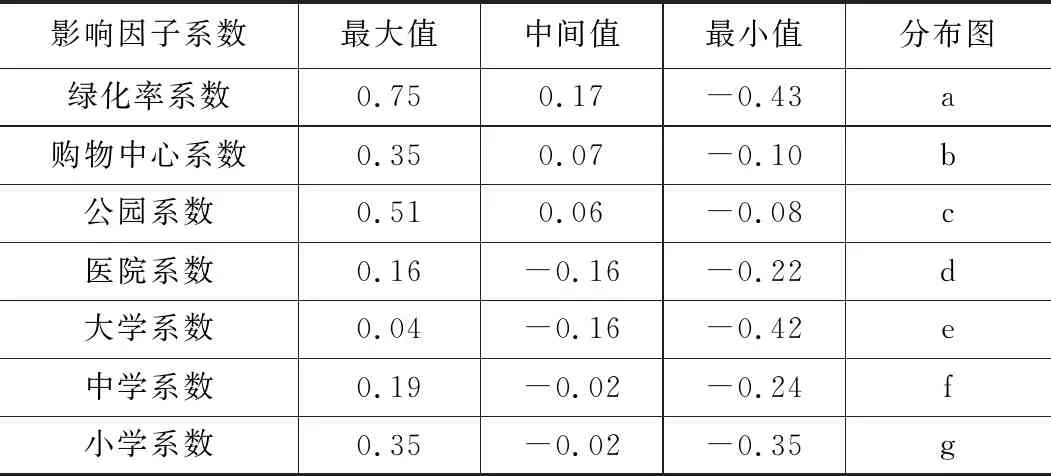
各因子热度分析成果表 表5

总体上看，上述影响因素与住宅价格都具有相关性，但影响程度并不一致，有些甚至表现一定的负相关。在老城区，绿化率、购物中心、公园、小学与住宅价格总体呈正相关，绿化率越高、购物中心分布越广、公园数越多，具备小学学区，小区住宅价格一般越高。其中绿化率、购物中心、公园、小学相关系数最大分别为0.75、0.35、0.51、0.35，可能原因在于老城区具有住宅密集、人流量大、活动空间紧凑、学位资源紧张等特征有关。在新城区，绿化率和住宅价格有负相关关系，说明在新城区绿化率和住宅价格没有必然的联系，原因可能在于新建小区环境相近且相对较好。

同时，可以看出公园对住宅价格的影响由西向东递增，从老城区到新城区对住宅价格的影响越来越大，原因在于新城区范围内公园数量不足造成的。医院、大学、中学对住宅价格几乎不产生影响，相关系数分布没有规律可循。特别是城市周边的小区，医院距离对其住宅价格的影响可以忽略不计，交通便利是造成这一现象的主要原因。考虑选取样本所在辖区高校数量较少，人数总量偏低以及中考不存在就近入读等因素，大学、中学与周围小区住宅价格影响极小。

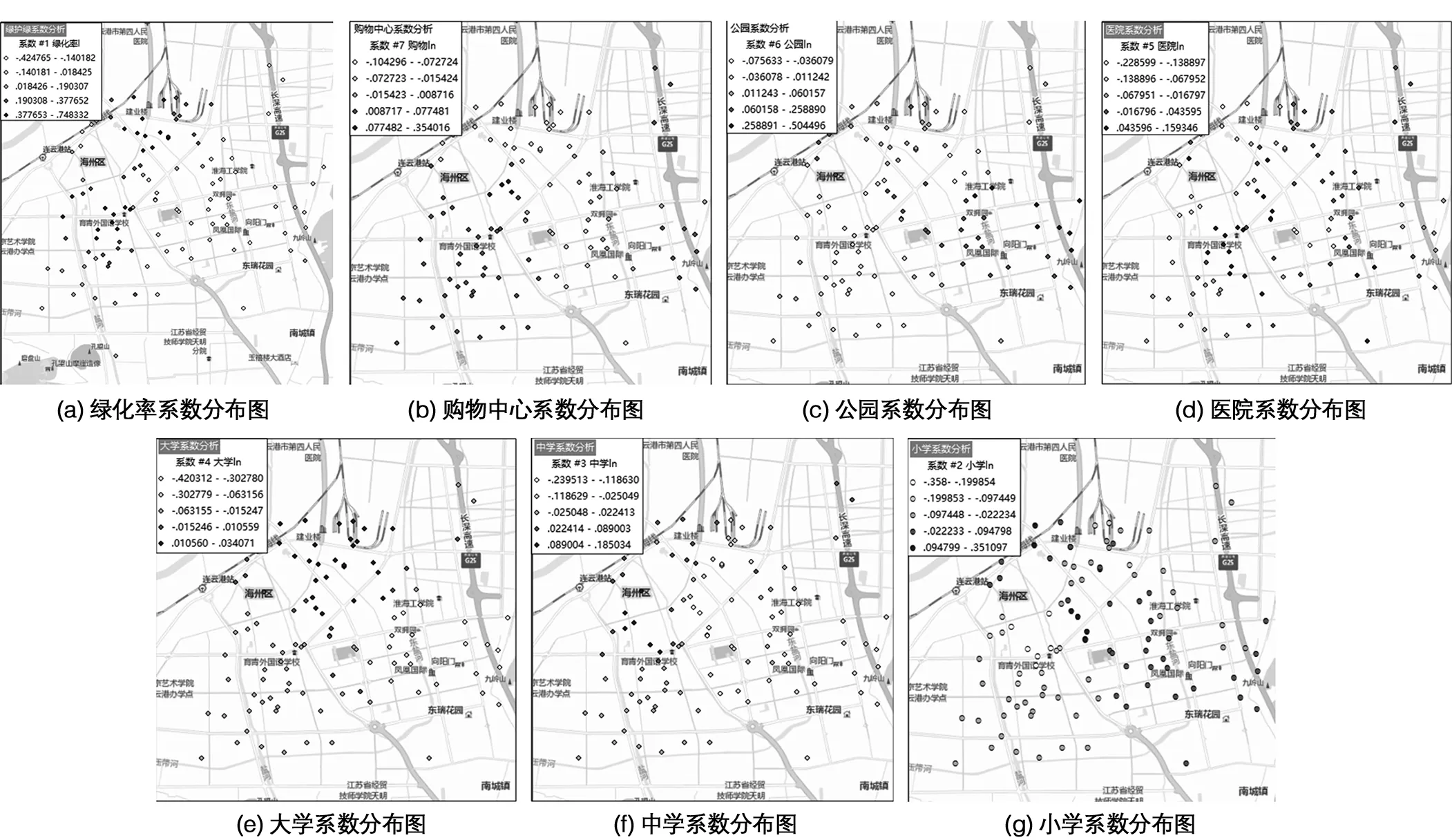
图1城市住宅价格各因子热度分析图

4 结 语

本文通过采集某辖区124个小区的住宅价格数据，通过构建地理加权回归模型，揭示小区住宅价格的空间分异和不同因子的影响，解决了回归系数随空间位置变化而变化的问题，但尚未解决回归系数随时间变化效应。目前，已有部分学者提出时空地理加权回归模型(GTWR)，但构建最优时空带宽及时空核函数等关键技术以减少模型的位置参数、降低拟合的计算量等方面，需要进一步研究。