锤炼方案 凝练模型 提炼思维
——以“倍增问题”的图式教学为例
2019-07-05张若静
□ 张若静
“倍增问题”即我们熟悉的“打电话”问题,是人教版五年级下册的一节综合实践课。在四年级上册的“数学广角”中,教材安排了有关优化思想的学习,让学生尝试在解决问题的多种方案中寻找最优的方案,初步体会运筹思想在实际生活中的应用,为“倍增问题”的教学打下了基础。
在教学调查中笔者发现以下几点问题:第一,打电话的情境设置离学生的现实经验比较远,不利于学生思考方案和建立模型;第二,运用表格进行解题时,要先列表再求解,相当麻烦;第三,学生在建模后的表述仍然不是很清晰,也就是说学生的思维是混乱不清的。
针对这样的问题,笔者对教学进行了以下思考。
一、择优选择情境,对比不同课题
基于学生的生活经验,针对“打电话”情境,学生会考虑现实操作的问题,如怎么知道谁被通知了,谁没有被通知?课堂上最优方案的制定也比较困难。基于这样的学情,笔者没有沿用教材中的情境,而将情境换成学生生活中熟悉的游戏——触碰救人。
问题情境改了,课题就得随着改。之所以选“倍增问题”作为课题,是因为“打电话”这一课题所关注的只是如何解决打电话问题,而“倍增问题”所关注的是具有倍增模式的一系列问题。
“倍增问题”这一课题对学生来说更具数学味。“触碰救人”的游戏情境,既抓住学生的兴趣点,又能更好地激发学生去思考,学生最优方案的制定很轻松,为本节课开了一个好头。两个课题给学生留下的课堂痕迹也不同,“打电话”给学生留下的是一个情境的内容,而“倍增问题”给学生留下的是一个数学模型。
(一)巧用情境,游戏激趣
1.出示游戏,讲解游戏
今天的学习就从老师编的数学游戏开始,什么游戏呢?——触碰救人。你们都是木头人,老师是自由人。如果老师碰一下某个同学,这个同学就被解救了,他也就成为自由人。当然,这个游戏有规则:一次只能解救1位同学。如果1秒钟解救1名同学,老师要尽快解救全班31名同学。你估计至少要多少秒能解救全班同学?此时,学生会异口同声地回答31秒。
2.猜游戏时间
为了让游戏更有意思,增加它的思维含量,我们规定:被解救的人,也可以去解救其他木头人。现在,按这样的规则再去解救全班同学,你觉得要多少秒?学生任意猜想,比较集中的答案是20秒、15秒、7秒。利用学生熟悉的游戏情境,设定游戏规则,通过猜想,初步感知游戏中的数学味。
(二)降阶游戏,化繁为简
如何尽快解救全班31个同学?这个问题还是比较复杂的,因为人数比较多,研究这样的问题,怎么入手会比较好一些呢?教师要引导学生学会化繁为简,从小数据入手,先解救7名同学,这样能有效激发学生寻求解决问题策略的热情。
二、关注学生生成,点拨优化方案
建立模型之前,方案的设计尤为重要。好的方案,能为模型的建立提供事半功倍的效果。
(一)自主探究,设计方案
1.设计方案
同样的游戏先解救7名同学,为这个问题设计
一个方案。

课中,捕捉学生的生成,利用学生的生成为新课的展开排兵布阵。一般学生的生成都不会超过7秒,7秒、6秒、5秒、4秒、3秒的结果都会出来。如下图所示。
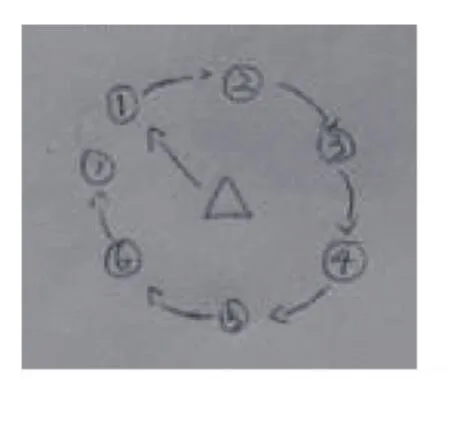
图1 7秒的方案
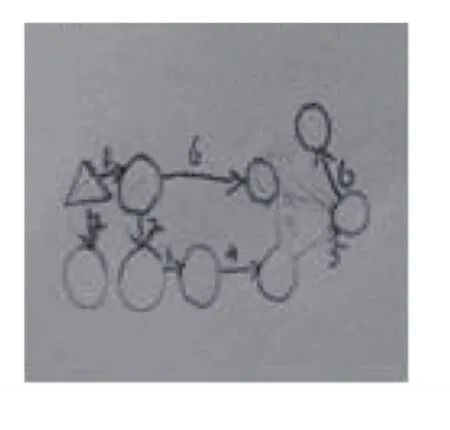
图2 6秒的方案

图3 5秒的方案

图4 4秒的方案

图5 4秒的方案

图6 3秒的方案
2.反馈交流
(1)反馈7秒、6秒、5秒、4秒等方案,同时请设计的同学来摆一摆。学生作品如下:
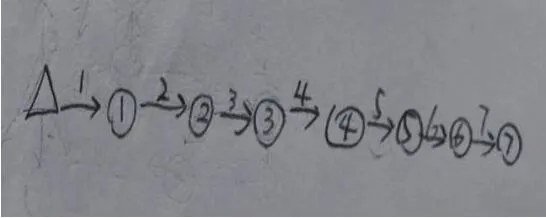
7秒的方案(秒数在线上)
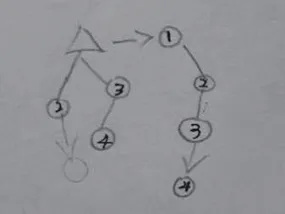
4秒的方案(秒数在圈圈内)
(2)反馈3秒的方案。

生1用隔线表示被解救的人
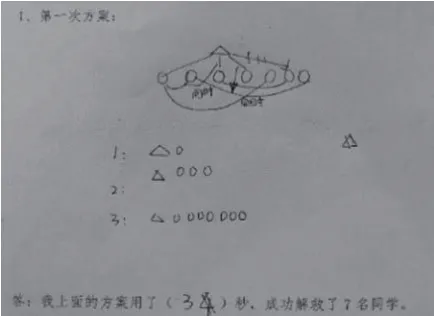
生2用个数表示被解救的人

生3用箭头连接被解救的人
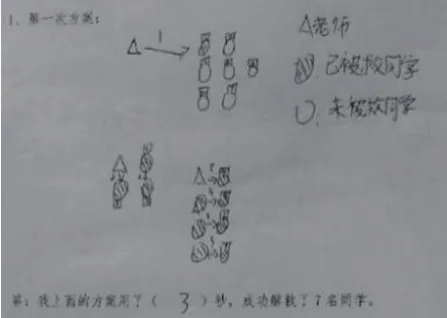
生4用阴影表示被解救的人
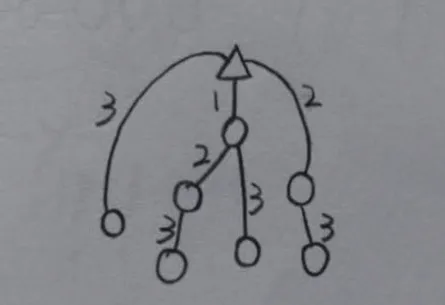
生5无序完整的解救图
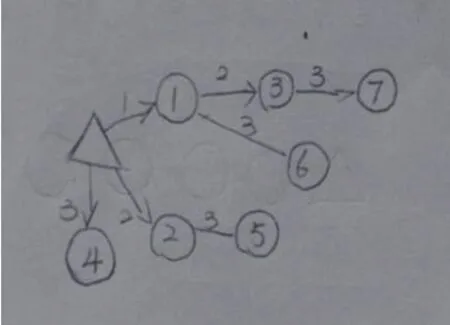
生6无序完整的解救图
3秒的方案很重要,教师可根据反馈及时追问:这幅图中第2秒有几个人去救?第3秒有几个人去救?给学生充分的时间进行方案的设计,静下心来思考解决问题的策略。抓住学生的生成,让反馈的学生上台说一说、摆一摆自己的方案,能非常清晰地展现学生的思维过程。可见,方案的呈现不能只是静态的结果,要有动态的生成过程。
(二)对比优化,锤炼方案
1.对比优化
从中选两个方案进行对比,一个是最优一个不是最优的,探究4秒(或其他几秒)的方案的时间为什么会多了,原因在哪里。从解决问题的方案中寻找“触碰救人”的最优方案,发现事物隐含的规律,为抽象出模型做铺垫。

不优方案
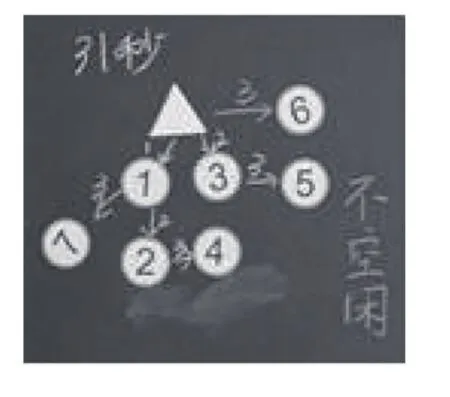
最优方案(不空闲)
2.提炼关键点
想要设计的方案时间最短,最关键的是“不空闲”“不浪费”等。在对比最优方案和不优方案的同时,提炼出关键点“每个自由人都不能空闲”。
三、渗透有序策略,修改理清方案
(一)理解方案,修改方案,画第3秒方案
板书上方案的修改是面向全班的,如果要深入个人,就要放手让学生独自修改方案。在修改方案之前,要先渗透“有序”的思考策略,而有序的方式主要采用箭头线来呈现。在理解第1秒、第2秒分别解救了几个人的基础上,请学生按照句式说一说,使学生的语言表述更清晰,思维更严谨。同时课件动态呈现箭头线辅助理解。按照这样的解救方案,让学生拿出学习单修改方案,同时思考第3秒的解救方案并画一画。通过这样的引导,学生就能轻松驾驭这些自主操作了。
学生修改的作品都挺不错,说明他们将最优化和有序都很好地进行了把控。如下图所示。
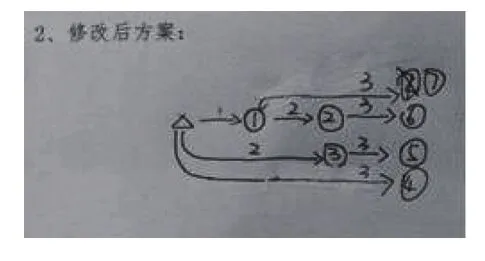
修改方案1
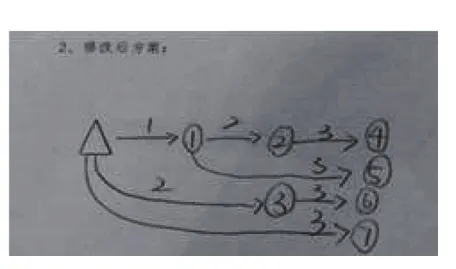
修改方案2
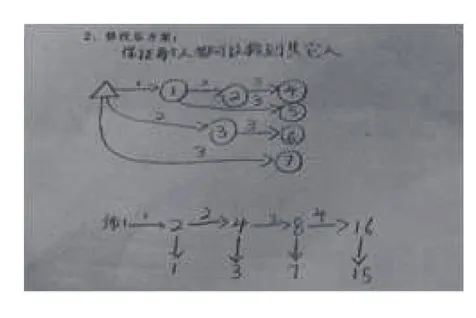
修改方案3
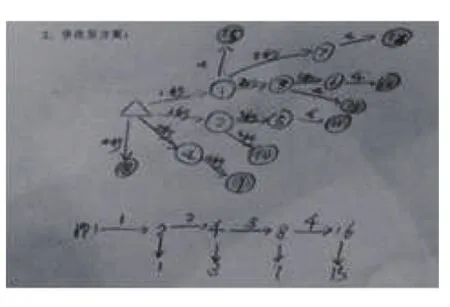
修改方案4
在“触碰救人”游戏中,在理解第1秒、第2秒怎么解救的基础上,教师引导学生规范有序地思考作图,同时修改自己原先的方案,画一画第3秒的解救情形,呈现3秒内有层次感的直观图。这样整齐美观的符号图完美地展现了最大限度利用时间的策略,也帮助学生更好地理解了解救7个人至少要3秒,达到了数形结合的效果。
(二)思考第4秒方案,将图式数据化
按照最优的解救策略,让学生思考第4秒的情形。学生不难发现前面有8个自由人,就可以解救8个人,课件随之出示箭头线。
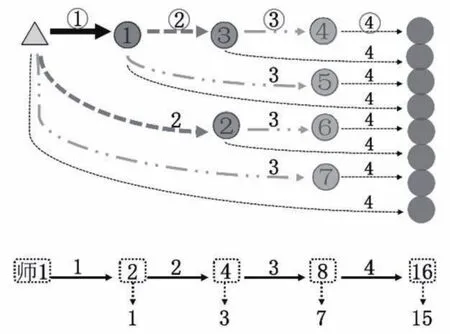
将直观图数据化,形成一条数据线,抽象出模型。因为有直观图做支撑,学生理解数据线上的每个数据都非常轻松。
四、弱化表格模式,提炼数据线模型
在之前的教学中,一旦渗透表格就异常困难,所以教师就试着弱化表格,构造一个让学生掌握起来更方便、更容易上手的模型。如下图的“数据线模型”:

这个线性模型对比表格的优势是:首先,线性的结构更有利于学生内化模型;其次,突出了主干上倍增的数据,使学生易于发现规律;再次,应用起来容易上手,不会像表格那样繁杂,遇到类似的一系列问题都能用这个模型来解决。
运用这样的模型解题,解救全班31个人,学生沿用数据线,很快能得到答案——5秒。继而可以延伸到如果全班是20人要多少秒?18人?15人?……在哪一个范围之内的人数都可以是用5秒?可见,抽象出数据线模型后,学生运用模型来解题就非常容易,同时还学会了寻找5秒能解救的区间数,学会了找起点和终点。
五、演绎倍增奥秘,应用模型解题
除了学生设计的符号图、有序的板书直观图,课中还运用了方格图来演示倍增的过程,给学生带来了强烈的视觉冲击,在学生脑海里留下了生动的、形象的数学模型。
(一)动图演示,发现规律
1.找规律
学生发现的规律:①自由人数都是2倍2倍地增加;②被解救的人数都比自由人数少1,少掉的人是老师;③自由人数和秒数之间的关系:第N秒,自由人数等于N个2相乘的积。
2.倍增动图
课件演示方格图翻倍的现象,揭示这种翻倍的现象,其实就是数学里面要研究的“倍增问题”。
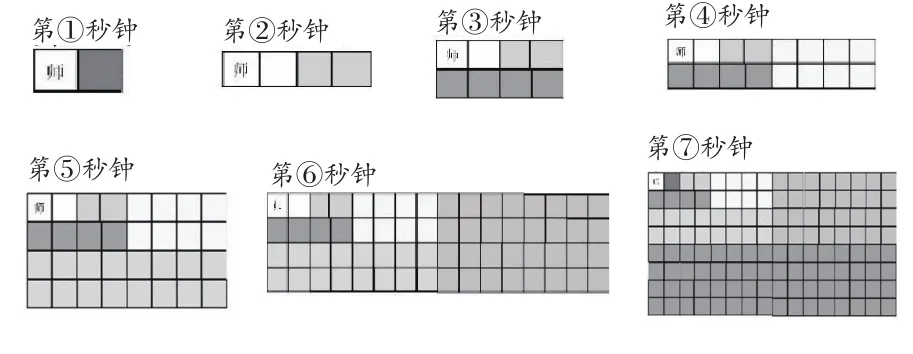
让学生从数据上感悟到翻倍的道理,通过方格图的演示让学生体验倍增惊人的结果,感受到翻倍的视觉震撼,感慨数学的神奇力量。
(二)应用模型,探试规律
1.模型的应用
有了以上各种表征方式的铺垫,让学生应用数据线模型解决解救200人需要多少秒的问题就变得容易多了。学生解题方式如下:
方式一:纯数据线
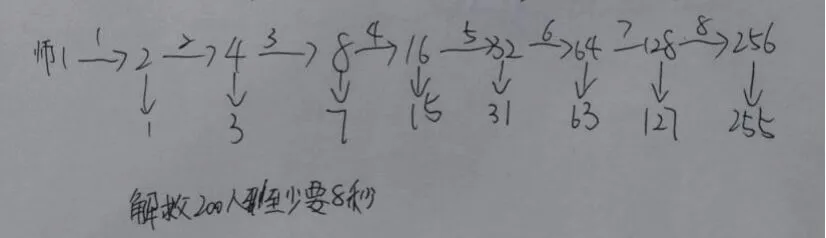
方式二:纯算式

方式三:数据线和算式相结合
这三种方式,表达形式不同,但思路是相似的,都共通着一样的解题思维——翻倍。有的学生从第1秒开始思考,有的学生比较机灵,借助前一秒的自由人数继续解题,都是值得嘉奖的,都将倍增模型运用得得心应手。
除了求解救200人需要多少秒的练习,还可以继续追问8秒能解救的人数范围是多少,进而思考8秒解救的区间数,让学生的思维迸发达到高潮。
2.生活中的倍增
一个古印度的故事。在一张棋盘的第1个小格内放1粒米,在第2个小格内放2粒,在第3个小格内放4粒,照这样放下去,每一小格内都比前一小格增加了1倍。到第64格时,到底要放多少粒米呢?体验一个小小的1经过不断的倍增,变成了大大的数据,让学生深深感叹倍增神奇的力量。同时,介绍生活当中其他的倍增现象,如:浮萍的生长、细胞的分裂等。让学生知道生活中有很多领域都会运用到倍增的数学规律。
综上,通过斟酌情境、巧妙设计、有序引导,学生建立模型、发现规律、应用规律,都水到渠成。鉴于多方位多角度地演绎,同时提供丰富的内容,构建生动的表象,学生扎实牢固地掌握了倍增模型。数学思想得到了渗透,思维能力得到了培养,核心素养得到了很好的彰显。
