执行器饱和不确定多智能体系统的一致性

景 丽, 李宏宇

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

0 引 言

多智能体系统是由多个相互作用的智能体组成的集合。目前在无人机编队、航天工程、无线传感器网络、通信工程等工业、军事及经济的各个领域有着广泛的应用,是控制工程等领域的研究热点。在多智能体系统的分布式协调控制问题中,主要研究多智能体系统的群集问题、编队问题和一致性问题[1]。一致性问题又是群集问题和编队问题的基础,所以对多智能体系统一致性的研究显得尤为重要。一致性是指随着时间的变化多智能体系统里的每个智能体的某一项状态量最终都能趋于一致。然而在实际的应用中,饱和约束是一个很普遍的现象。如果不考虑饱和约束对系统性能的影响将有可能发生严重的事故[2]。在实际的饱和受限控制系统中,执行器饱和和输入饱和是最为常见的。对于饱和项的常见处理方法有扇形区域法[3]、饱和度法[4-5]、凸组合法(H矩阵法)[6-7]。对于饱和约束多智能体系统的一致性问题,学者们提出了许多的方法,如小增益反馈法[8-10]、S-procedure法[11]等。著名学者Lin等[12]提出的小增益反馈法有2种,一种是特征根结构的配置方法,另一种是参数Riccati方程法。后来人们又在改进小增益反馈法的基础上提出了低-高增益反馈法[13]。然而实际的控制系统本身往往也会带有一定不确定性的,本文针对实际多智能体系统中不可避免的执行器饱和约束和自身具有的不确定性,设计一致性控制律,得到多智能体系统可以达到领航-跟随模型下半全局一致性的条件。

本文主要研究一类执行器饱和多智能体系统的一致性问题,采用凸组合的方法处理饱和项,并进行吸引域估计。应用Lyapunov稳定性理论,并运用MATLAB线性矩阵不等式等进行研究。

1 预备知识

图论知识和Kronecker积是研究多智能体系统一致性问题的主要工具。下面给出相关定义和引理[12]。

图是二元组G=(V,E),其中V是节点集,E是边集。V={1,2,…,N}表示N个节点代表N个智能体,E⊆{(i,j):i,j∈V,i≠j}表示智能体之间的信息传递。如果(j,i)是有向图的一个边则eij≠0,否则eij=0。如果eij=eji,则该图为无向图。

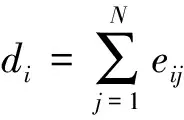
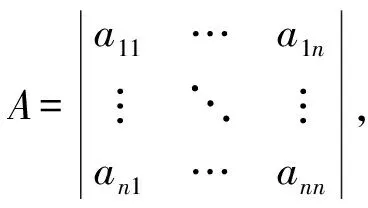
拉普拉斯矩阵L=D-A,无向图L为对称矩阵。如果从一个根节点把信息传递到图中其他所有节点,则这个图含有一棵生成树。

引理1 令图G对应的拉普拉斯矩阵为L,下面结论成立:

1) 0是矩阵L的一个特征根,1N为矩阵L对应于特征根0的右特征向量;

2) 如果图G含有一个有向生成树,则特征根0的代数重数为1,且矩阵L的其他特征根都具有负实部。

3) 如果图G是强连通的,则存在一个正的列向量ω满足ωTL=0。

4) 如果G是无向的连通图当且仅当矩阵L的次小特征根为正实数。

Kronecker积性质

设A,B,C,D为适维矩阵,则有:

1) (αA)⊗B=A⊗(αB),其中α为常数 ;

2) (A+B)⊗C=A⊗C+B⊗C;

3) (A⊗B)(C⊗D)=(AC⊗BD);

4) (A⊗B)T=AT⊗BT;

引理2 凸组合法[14](H矩阵法)给定适维矩阵F,H∈Rm×n,如果x∈L(H),则

“co”表示凸包,

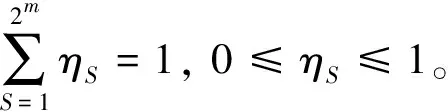
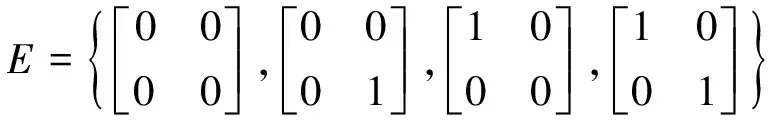
引理3[15]对任意适维矩阵X,Y和任意实数ε>0,有下式成立:

XTY+YTX≤ε-1XTX+εYTY

定义1 椭球集合[16]:P>0,P∈Rn×n,ρ>0为标量,定义椭球体

ε(P,ρ)={x∈Rn:xTPx≤ρ}

定义2 多面体集合[16]:L(H)={x∈Rn:hjx≤1,j=1,2,…,m}是一个多面体集合。其中hj为H第j行。

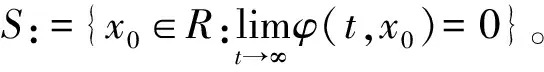
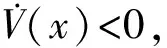
2 系统描述

考虑一个由N个跟随智能体和一个领航智能体组成的N+1个带有不确定项的多智能体系统,其中每个跟随智能体的状态向量为xi∈n,控制输入为ui∈m。则跟随智能体的状态方程为

xi=(A+ΔA)xi+Bδ(ui),i=1,…,N

(1)

其中:A∈n×n,B∈n×m。假设(A,B)可控,不确定矩阵ΔA=MN,T≤I,M,N为适维矩阵,sat(·)表示饱和非线性函数,记为δ(·),定义如下:

领航智能体的状态方程为

(2)

每个跟随智能体与领航智能体的状态差为

(3)

则设跟随智能体与领航智能体的整体状态差为

(4)

为了研究多智能体系统一致性问题,需要以下内容[12]。

假设1 领航智能体与跟随智能体组成的图包含一个生成树。

假设2 矩阵対(A,B)可控的。

3 主要结果

3.1 执行器饱和多智能体系统半全局一致性

定理1 假设1和假设2成立,设一致性控制算法:

(5)

下,如果

成立,则带有不确定项的执行器饱和多智能体系统(7)可以达到领航-跟随模型下半全局一致性。其中λmax为C的最大特征值,C=L+B0。

证明 由图论知识及Kronecker积,在控制律(5)下多智能体系统整体可以写成

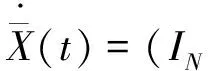
(7)

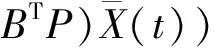
(8)

则多智能体系统改写为

(9)

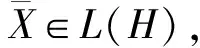
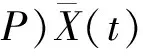
(10)

则

其中

则领航-跟随模型多智能体系统达到半全局一致性。证毕。

3.2 控制器设计

定理2 考虑由模型(1)、(2)在给定控制律(5)下构成的多智能体系统(7),如果存在P>0及正数ε1,ε2,ε3,使得如下不等式:

(11)

成立且满足ε(IN⊗P,1)⊂L(H),其中

则存在增益矩阵F=C⊗BTP,使得系统(7)达到半全局一致性。

证明 根据Schur引理,式(6)与式(12)等价,

(12)

其中

令

T=diag{I⊗P-1,I,I}

对式(12)左右两边分别乘以TT和T,则

I⊗P-1=I⊗P*,H(I⊗P-1)=H*,N(I⊗P-1)=N*

于是式(11)成立。

3.3 吸引域估计

估计最大吸引域问题可以转化为如下最优化问题:

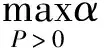
(a)式等价于IN⊗P-α-2R≤0⟺α-2R-IN⊗P≥0;

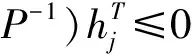
设γ=α-2,得到

以上可以用LMI方法求解。

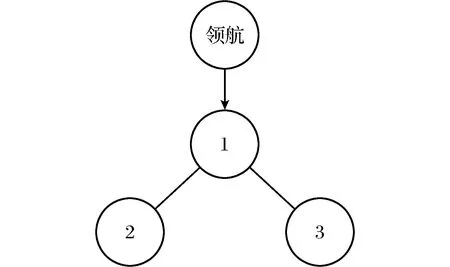
图1 领航-跟随模型多智能体系统Fig.1 The graph of leader-follower model multi-agent system

4 数值仿真

考虑多智能体系统(7),其参数为

多智能体系统(7)拓扑结构如图1所示。

根据定理2利用MATLAB的LMI工具箱求得

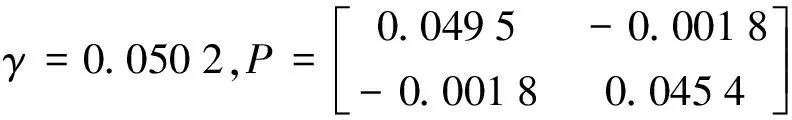
增益矩阵F

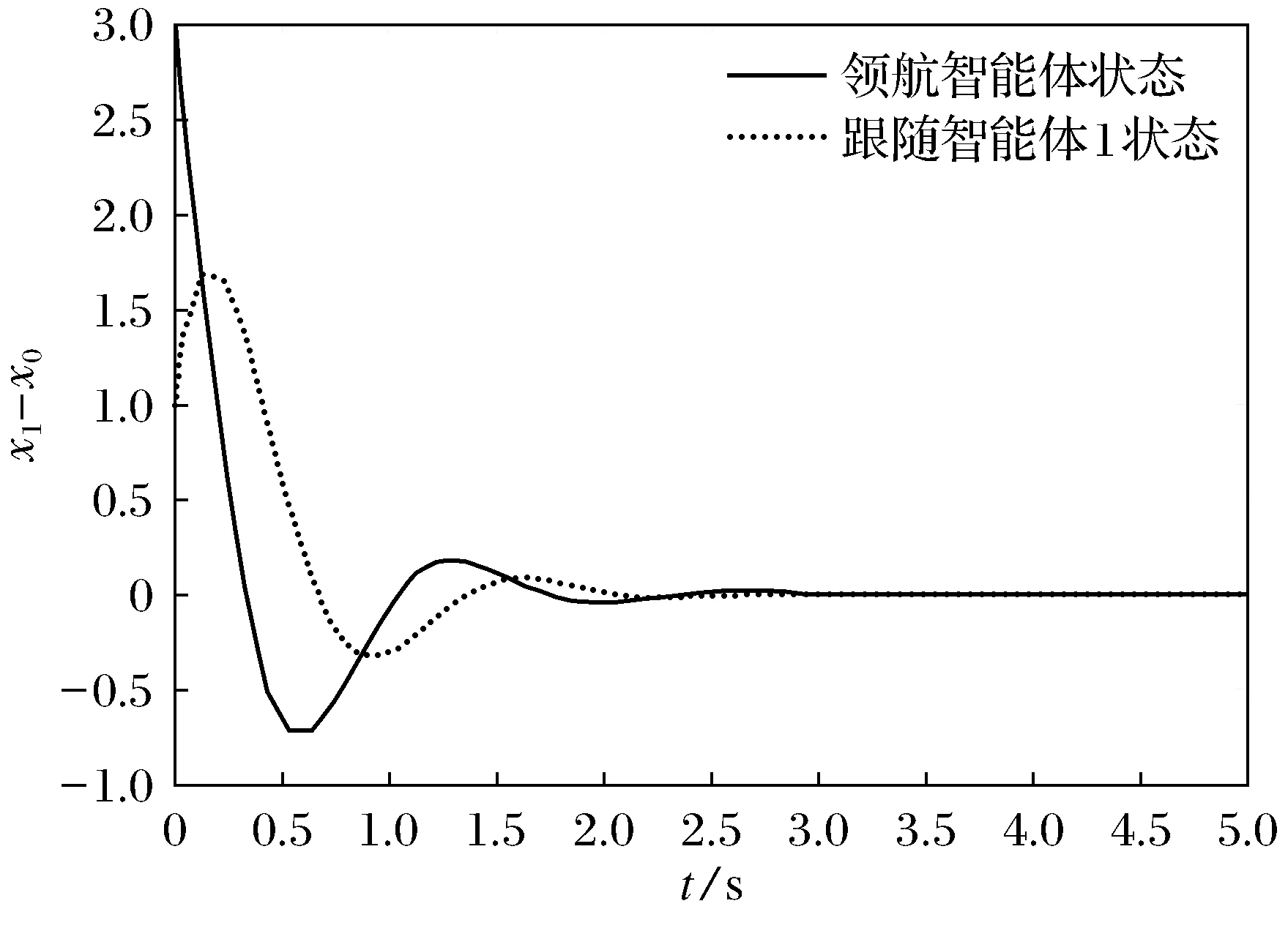
图2 跟随智能体1与领航智能体的状态差曲线

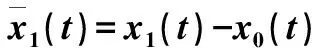
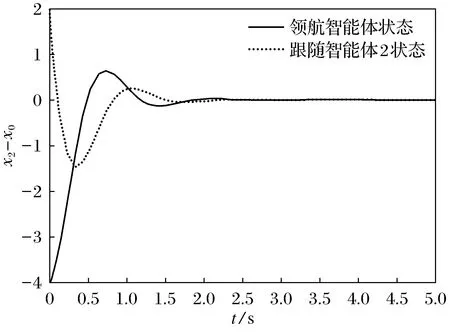
图3 跟随智能体2与领航智能体的状态差曲线

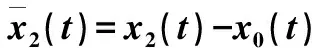
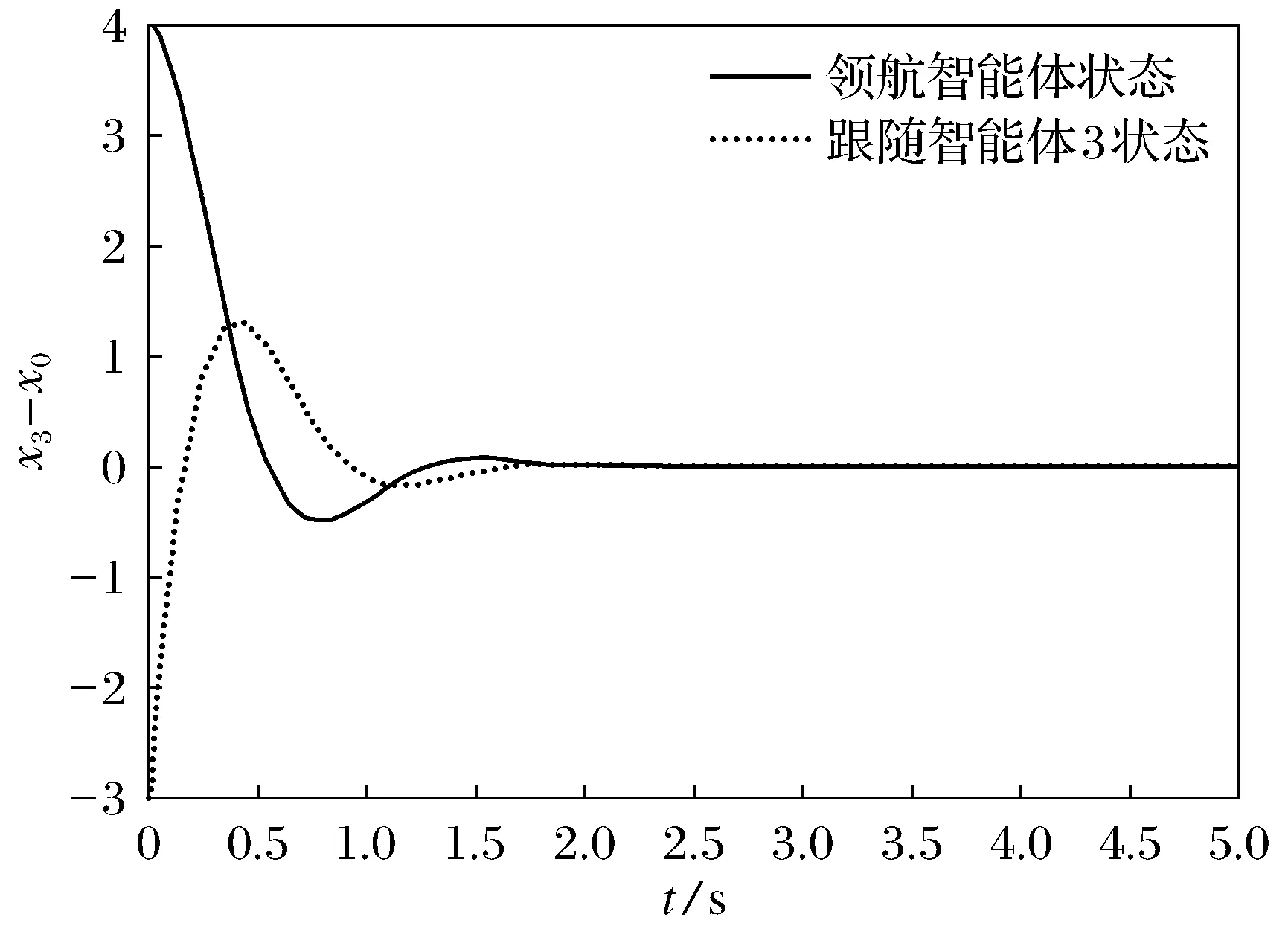
图4 跟随智能体3与领航智能体的状态差曲线

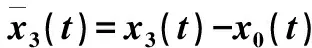
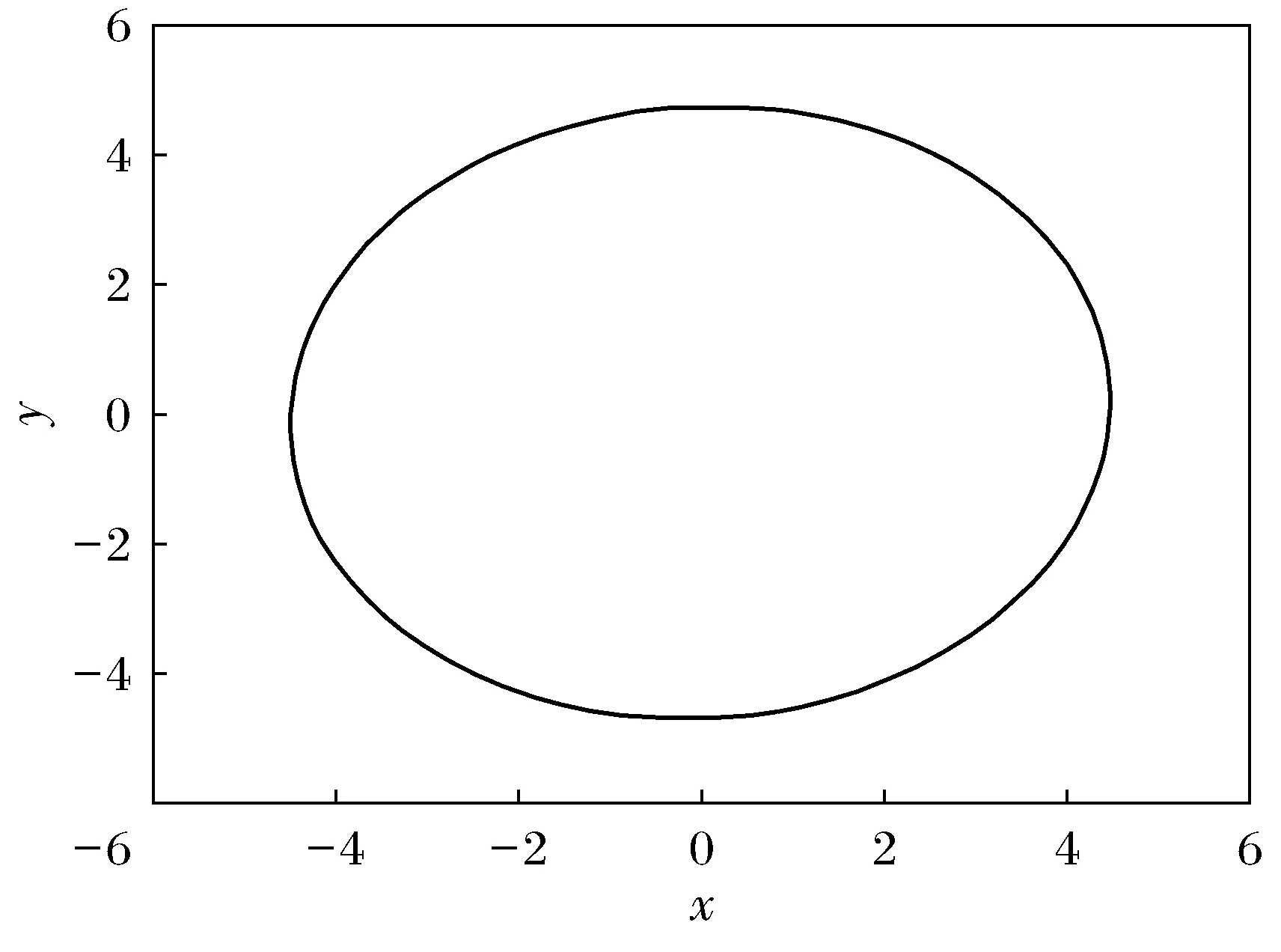
图5 系统吸引域估计Fig.5 Estimation of system attraction domain

5 结 论

本文研究一类执行器饱和不确定的线性多智能体系统的一致性问题,应用Lyapunov稳定性理论,选取合适的V函数,采用凸组合的方法处理饱和项,得到了执行器饱和不确定线性多智能体系统的半全局一致性结论并进行吸引域估计,并给出算例,运用MATLAB线性矩阵不等式工具箱和Simulink工具箱进行仿真,验证文中结论。