省级电力公司电网物资配送中心选址优化决策研究

周鹏程，程怡心，吴南南，王晟嫣

（1.华北电力大学 经济与管理学院，北京 102206；2.华北电力大学 控制与计算机工程学院，北京 102206）

0 引言

电网物资作为电力公司核心资源之一，是企业经营发展战略的重要组成部分。电网物资管理的关键是保证仓储中的物资能够及时、安全、准确地到达需求点。配送中心是连接电网物资公司或供应商与其下游的物资需求企业的关键性枢纽。配送中心的选址是否得当，直接影响电力企业的物流服务水平和配送效率高低，关系到电网整体运行的安全性和经济性。

国家电网有限公司全面开展物资集约化管理，在加快“三型两网”战略建设的背景下，实施物资标准化，开展统一的仓储配送布局，建立快捷高效的配送网络，引入配送作业智能终端，打造配送调度管理系统。南方电网公司提出了构建仓库层级扁平、库存结构及定额合理、标准化跨区域配送、服务功能齐全的“大仓库、大配送”管理模式，通过高效实时的物资管理信息系统，建立跨供电局的区域性仓库，形成流转顺畅的配送网络，保证物资储备合理、运作高效、服务到位，实现系统内动态快捷地横向调拨物资。科学、合理地规划电网物资配送中心是提高物流管理水平与资源利用率、降低运行成本、提升企业管理水平的关键举措。

在综合考虑配送中心选址影响因素的基础上，提出并建立配送中心选址多层次维度的评价指标体系，并基于IAHP-COWA法进行组合赋权优化。构建基于FCE的配送中心选址优化模型，对候选地址进行打分评价。将综合评分值作为目标函数之一，建立电网物资配送中心选址多目标优化模型，并基于NSGA-Ⅱ算法求解多目标函数，最终得出物资配送中心选址与配送方案，为省级电力公司降低配送成本、提升配送效率、提高电网物资集约化水平提供决策依据。

1 省级电力公司配送中心选址指标体系

1.1 配送中心选址指标体系构建

电网物资配送具有特殊性，针对电力物资的配送组织架构和采购供应流程，在配送中心选址规划时要重点分析各备选地址的优势与劣势，综合考虑各类影响因素，包括但不限于自然环境、经济环境、公共环境、物流环境等因素。

在进行电力物资配送中心选址规划时，需要考虑上述各因素之间的关系，既要保证电网故障、变电站停运情况下应急物资的供应，又要降低电力企业的物流成本。在考虑影响电网物资配送中心选址因素的基础上，从中选取16项指标构建了电网物资配送中心选址的评价指标体系，如表1所示。

表1 电网物资配送中心选址评价指标体系

1.2 评价指标规范化处理模型

由于所构建的电网物资配送中心选址评价指标体系是一个多层次多维度的综合评价体系，为便于比较，消除指标间单位和量级差异的影响，对指标矩阵进行规范化处理。

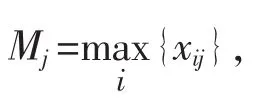
式中：xij为第i个指标的第j个数据取值。

2）针对中间型指标采用隶属函数法，处理公式为

式中：a，d 为函数的下、 上限；b，c 为适度区间［b，c］的区间最小、最大值，该值按照决策者对隶属度偏好的高低来决定。

2 省级电力公司配送中心选址评价决策

2.1 基于IAHP-COWA的组合赋权模型

2.1.1 IAHP法

改进层次分析法（Improved Analytic Hierarchy Process，IAHP）是一种将与决策有关的元素分解成目标、准则、方案等层次权重决策分析方法，并引入最优传递矩阵，更好地满足一致性检验的要求。

1）按元素的相互关系及其隶属关系形成不同的层次，同一层次的元素作为准则对下一层次的元素起支配作用，同时又受上一层次元素的支配，建立层次结构模型。

2）建立层次分析模型以后，要在各层元素中进行两两比较，构造出比较判断矩阵。为了使决策判断定量化，通常采用1～9标度方法形成判断矩阵，判断矩阵 Y=（yij）n×m如式（4）所示。

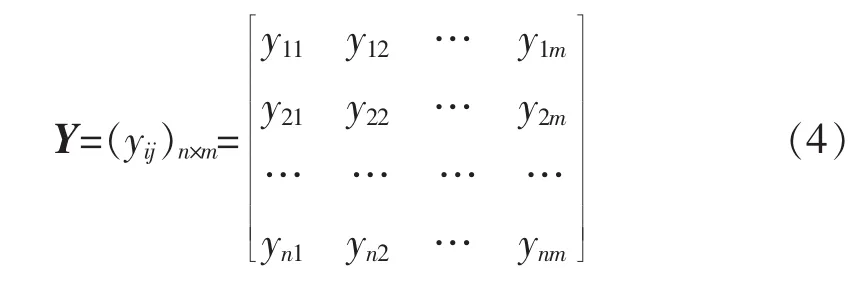
通过式（5）～（6），对判断矩阵中的元素进行变换，将原有的判断矩阵转换为 Z=（zij）n×m式中：n为判断矩阵的阶数。

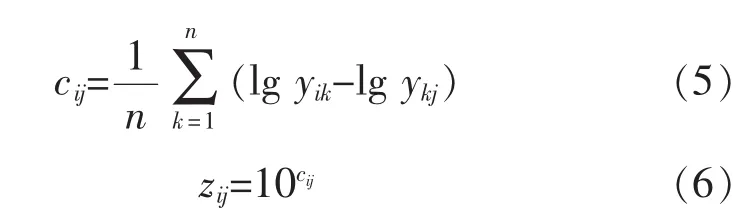
3）检验判断矩阵的随机一致性比例CR是否满足 CR＜0.1，若满足则通过一致性检验。 其中 CR=CI/RI，且 CI=（λ-n）/（n-1）。

4）计算各层次要素权重，并进行层次排序，即：

2.1.2 COWA法

基于组合数的有序加权算子 （Combination Ordered Weighted Aveaging，COWA）通过对决策数据重新排列，对不同位置的数据赋予不同的权重值，以减少极端数据的影响，使赋权更符合客观实际。

1）评价指标的决策数据集L可表示为｛a1，a2，…，an｝，按照从小到大顺序重新排列，排列后的数据集为｛b1，b2，…，bn｝。

2）根据组合数的性质对决策数据加权，得到加权向量为

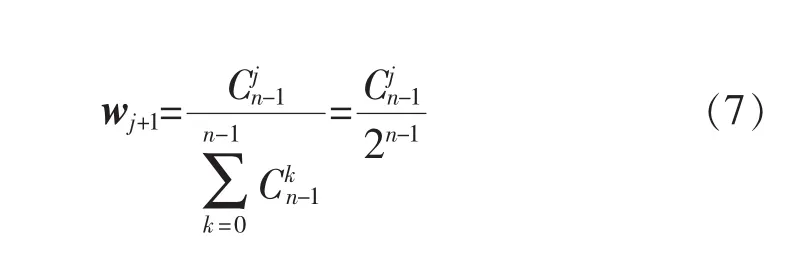
3）根据加权向量η对决策数据进行加权，得到评价指标的绝对权重值和相对权重值ηi为：

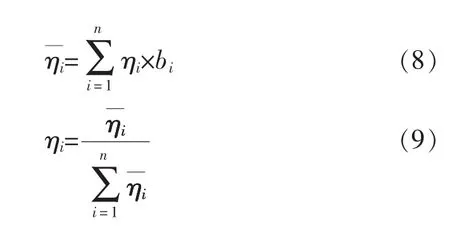
2.1.3 组合赋权优化

设μi为IAHP法得到的权重值，ηi为COWA法得到的权重值，引入距离函数，即

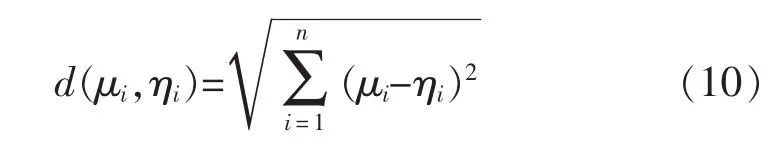
设组合权重为ξi，用线性加权法计算组合权重值，即

式中：y1和 y2为权重偏好系数，且满足 d2（μi，ηi）=（y1-y2）2，y1+y2=1。

2.2 基于FCE法的配送中心选址评价决策模型

模糊综合评价（Fuzzy Comprehensive Evaluation，FCE）能够从定性、定量角度去解决评价对象模糊性和多样性。为此，本文采用多级FCE法建立省级电力公司配送中心选址评价决策模型。

1）将所有评价指标分成m个因素集，建立因素集 U=｛U1，U2，…，Um｝，满足 Ui∩Uj=Ø（i≠j），再将 Ui划分为子因素集 Ui=｛Ui1，Ui2，…Uij，…，Uin｝。

2）根据指标的性质和程度，建立评价集V＝｛V1，V2，…，Vn｝，各元素Vi代表各种可能的总的评价结果，并构建评价矩阵 R=（rij）n×m，rij∈［0，1］。 给出 Ui中各评价指标的权重向量集 Ai=｛ai1，ai2，…，ain｝。

3）若对Ui的m个因素进行单因素评价后得到单因素评价矩阵Ri，采用相同的模糊算子将Ri和权重向量Ai模糊合成，计算出该层次因素集Ui的评价结果为

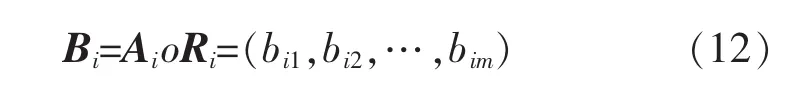
4）将Ui视为一个单独元素，Bi表示Ui的单指标评价向量，可构成U到V的模糊评价矩阵，即

由此假设，若 u1，u2，…，um的 权重向量为 Ai＝［a1，a2，…，an］，则 U 的综合评价为 Bi=AioRi=（bi1，bi2，…，bim）。将模糊综合评价结果B与评价集V进行模糊运算，确定智慧城市多能源系统利用综合效益评估的最优值。

3 省级电力公司配送中心选址多目标优化

3.1 配送中心选址多目标优化模型构建

3.1.1 基本假设

为更好地实现电网物资配送中心选址多目标优化需求，做如下基本假设：每个物资配送中心必须至少满足一个需求点；每个供应点必须至少满足一个物资配送中心；每个需求点为单一需求，且需求量已知；每个需求点和各备选配送中心之间、各备选配送中心和每个供应点之间的距离、单位运输成本已知，且运输成本和距离成正比；配送中心的土建成本、运输和配送成本、运营成本等已知；每个供应点、各备选物资配送中心有容量限制，且容量上限已知；物资配送中心的数量有限，且已知。

3.1.2 目标函数

1）配送中心选址的总成本最小

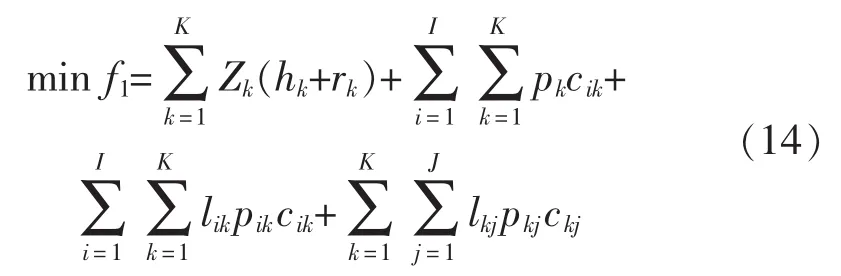
式中：I为物资供应点集合；K为物资配送中心备选点集合；J为物资需求点集合；hk为第k个物资配送中心建筑物年折旧费用；rk为第k个物资配送中心设施设备年折旧费用；pk为经物资配送中心流转的备品备件的单位管理成本；lik为供应点i到物资配送中心k的距离；lkj为物资配送中心k到需求点j的距离；pik为供应点i到物资配送中心k的单位平均运输成本；pkj为物资配送中心k到需求点j的单位平均运输成本；cij为需求点j的需求量；ckj为物资配送中心k向需求点j的配送量；cik为供应点i向物资配送中心k的供应量；Zk为决策变量，取值为1表示第k个地址被确定为物资配送中心，反之为0。

2）配送中心的低碳配送排放量最小

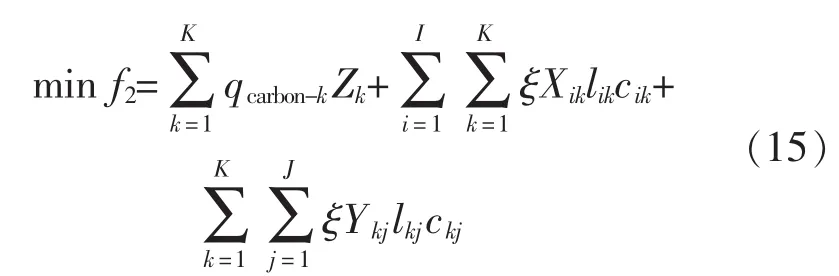
式中：qcarbon-k备选配送中心k固定的年CO2排放量；运输工具（货车）的CO2排放量系数；Xik为决策变量，取值为1表示第i个供应点向第k个物资配送中心供货，反之为0；Ykj为决策变量，取值为1表示第k个物资配送中心向第j个需求点配送，反之为0。

3）配送中心备选地址的评分值最高为

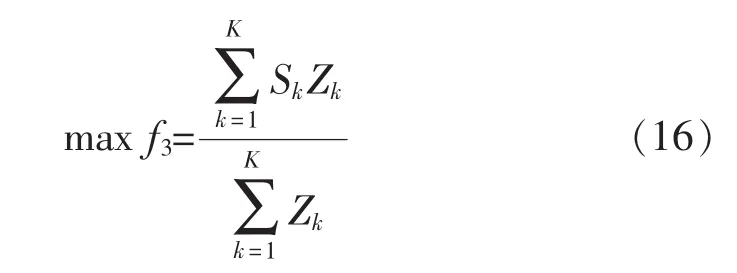
式中：Sk为物资配送中心备选地址的综合评价得分值。

3.1.3 约束条件

式（17）为第k个物资配送中心被选定后才能接受第i个供应点的供应；式（18）为第k个物资配送中心被选定后才能向第j个需求点的配送；式（19）为供应点i的供应量不能超过供应点的容量限制；式（20）为物资配送中心k的配送量不能超过配送中心的容量限制；式（21）为供应点i必须向至少一个物资配送中心供应；式（22）为物资配送中心k必须向至少一个需求点提供配送；式（23）～（25）为决策变量 Zk，Xik，Ykj的取值说明。

3.2 配送中心选址多目优化标模型求解

电网物资配送中心选址多目标优化是一个典型的NP-Hard问题。考虑的是电网物资配送网络中全局的最优化，采用具有良好鲁棒性和隐含并行特性的遗传算法（Genetic Algorithm，GA）对多目标优化模型求解。然而，各目标函数间存在冲突、无法比较的情况，求解结果通常存在一个解集称为Pareto前沿。为此，本文采用运行速度更快、解集收敛性更好的带精英策略的非支配排序遗传算法 （NSGA-II）、基于Pareto支配关系进行计算求解。

1）编码。

将决策变量编码成不同的字符串组成 （即不同的迭代点）。根据多目标优化模型的特点，分别对决策变量进行编码，当供应关系和配送关系确定后，根据需求点已知的需求量可求出决策变量中配送中心和需求点之间的配送量。

2）种群初始化。

NSGA-Ⅱ的种群初始化采用随机生产方法，初始种群的大小是NSGA-Ⅱ中需要设置的重要参数。参考相关文献，当初始种群规模设置为N∈［20，200］的迭代结果较为理想。

3）适应度函数。

对于F值最大化的目标函数，其适应度函数分别取为 Fit（F3）＝1－max f3，f3为备选地址的评价得分值的目标函数；对于F值最小化的目标函数，其适应度函数取为：Fit（F1）＝max f1和 Fit（F2）＝max f2，f1和f2分别为配送中心选址的总成本的目标函数和配送中心的低碳配送排放量。

4）非支配排序。

为在NSGA-Ⅱ迭代中搜寻到的非劣解，对目标函数f1进行惩罚，以便使迭代结果更有效，设置惩罚项A＝ε（Q*i-Qi），惩罚值A为超出供应点供应能力的部分乘以惩罚系数ε，并惩罚值A加入目标函数f1，即可对目标函数f2和f3和f1进行非支配排序。

5）遗传操作。

NSGA-Ⅱ染色体交换时采用均匀变异，根据事先设置的变异概率pa选择个体判断是否变异。通常，交叉概率 、变异概率 pc［0.44，0.99］，经多次迭代后，NSGA-Ⅱ算法中取 pc=0.9，pa=0.1。

4 省级电力公司配送中心选址算例分析

考虑到城市未来的配电网建设和运营需要，以及省级公司业务的发展，某省公司拟在电网物资供应点和需求点之间，开展本供电区域内的电网物资配送中心选址的工作，并确定3（U=3）个最优地点作为配送中心的最终地址进行施工建设。

4.1 指标规范化处理

为消除指标单位和量级的差异所带来的影响，避免得到不合理的评价结果，针对配送中心选址评价指标体系中的不同指标类型，需要对对指标矩阵进行规范化处理，指标规范化处理结果如表2所示。

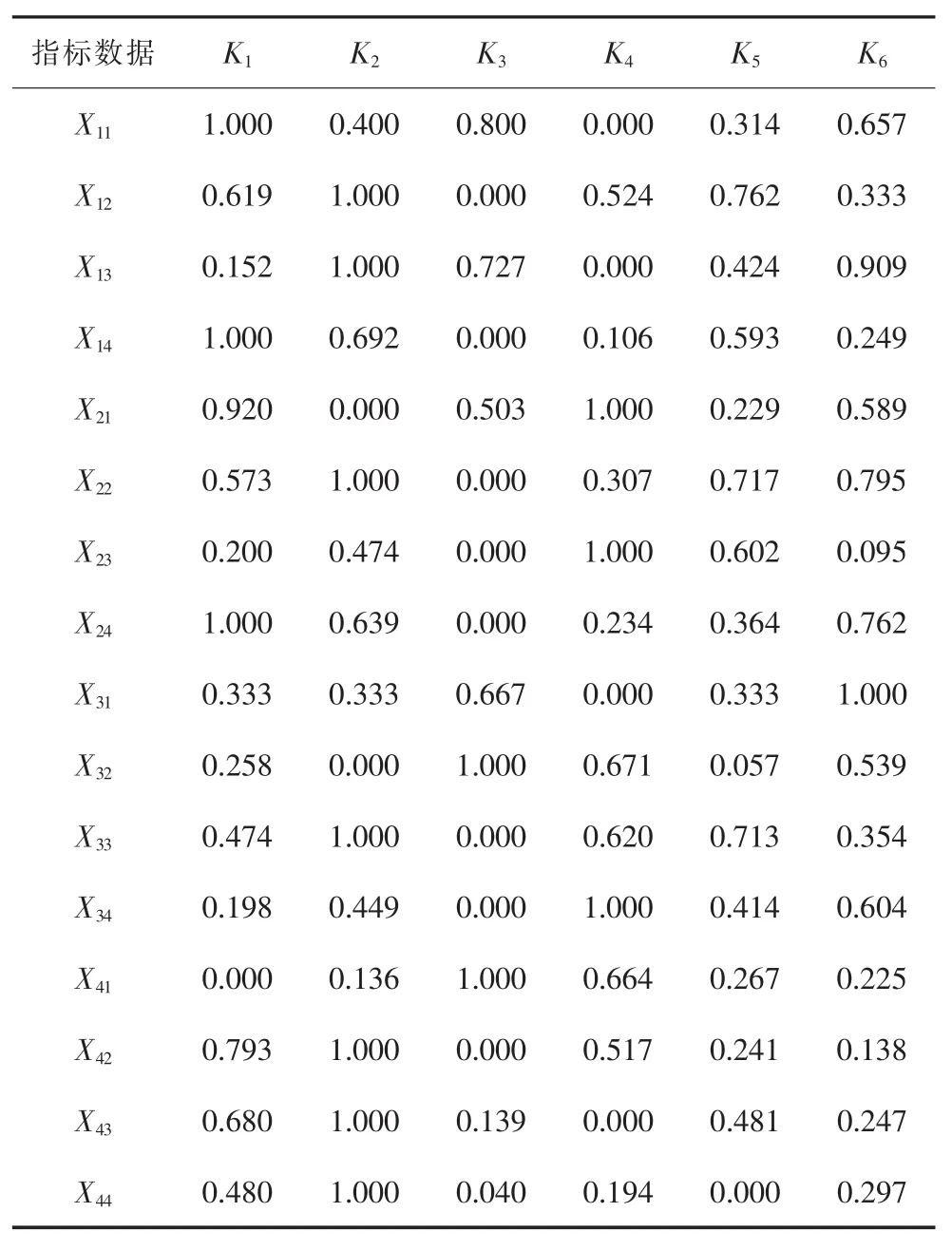
表2 配送中心的评价指标规范化处理结果

4.2 组合赋权模型权重求解

通过IAHP，COWA及组合赋权优化计算可得省级电力公司物资配送中心选址优化决策指标权重值如表3所示。

4.3 模糊综合评价模型求解

4.3.1 建立评价集

结合电网物资的特点和配送中心选址的相关要求，按照评标指标的性质和程度将其划分为5个等级。假设评价指标的评价集为 V=｛V1，V2，…，V5｝，其中，Vj为第 j个等级的分数；记 Vj＝｛优［80，100），良［60，80），中［40，60），较差［20，40），差［0，20）｝。 取等级分数区间的上限值构成评价集。

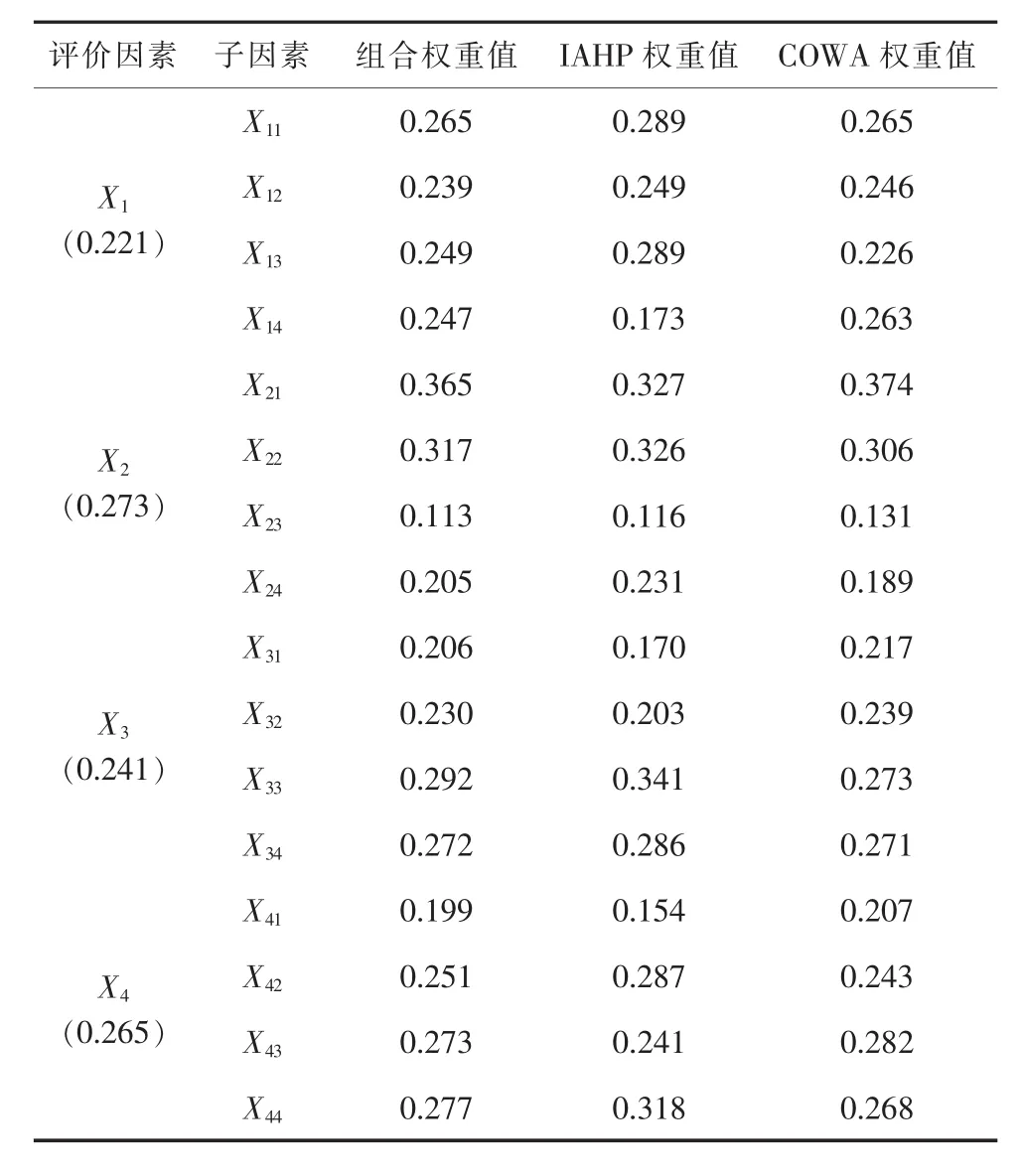
表3 评价指标体系的指标集及权重集

4.3.2 构建隶属度矩阵

假设邀请M位专家对单个因素ui进行评价。以候选配送中心K1为例，构造模糊隶属度矩阵如表4所示。

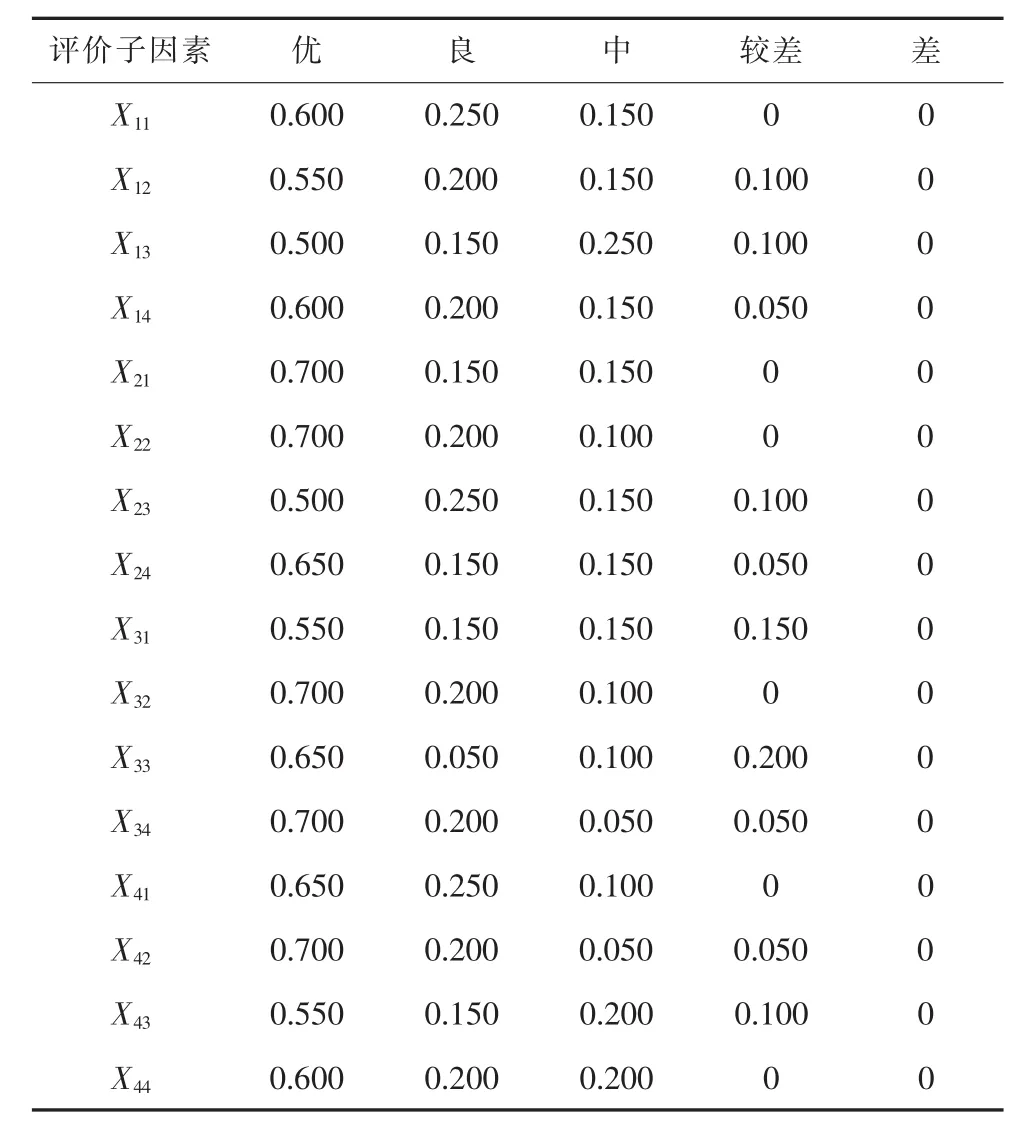
表4 配送中心K1模糊隶属度矩阵

4.3.3 进行模糊综合评判

当权重集A和单因素评价矩阵R为已知时，便可作模糊变换来进行综合评价，即由Bi=AioRi可求得第1层次因素集的模糊综合评价矩阵R为

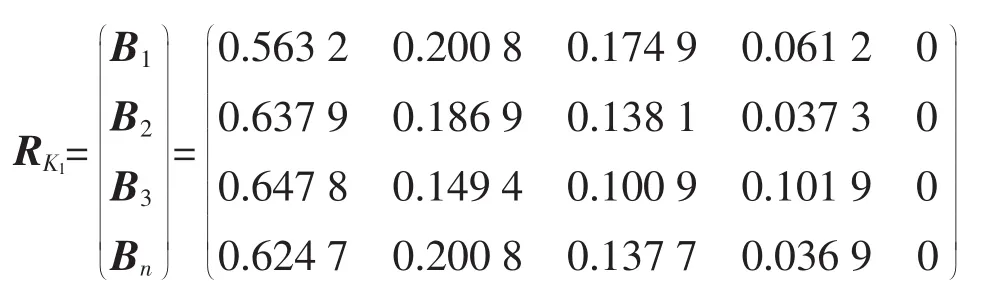
对RK1进行模糊运算可得，候选物资配送中心K1的模糊综合评判为 BK1=AoRK1=（0.620 3，0.184 6，0.137 1，0.058 0，0）。

4.3.4 综合评判结果

根据最大隶属度原则，候选物资配送中心K1的综合隶属度值为 0.620 3，评语为“优”，即：大约有62.03%的候选物资配送中心K1的选址地点满意，有94.20%的专家对其持认可态度（即评价得分为“中”及以上的）。

4.3.5 评价结果分值分析

基于综合评判结果，将各候选物资配送中心的评价结果分别转化为分值，则候选配送中心K1，K2，K3，K4，K5，K6的评价分值分别为87.34，90.55，90.42，90.00，89.63，89.87。对比分析评判结果和最终得分可知，候选物资配送中心的评价得分排序为K2＞K3＞K4＞K6＞K5＞K1。

4.4 多目标优化模型求解

4.4.1 各目标函数规范化处理

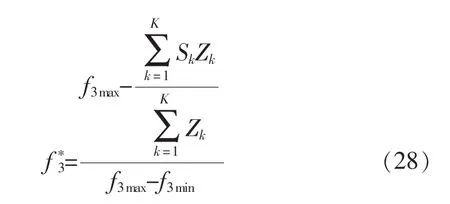
在将多目标模型转化为单目标模型过程中，由于各目标函数的量纲不一致，若没有进行统一量纲工作，则各目标函数间的数量级和含义相差较大，最终导致求解的配送中心选址优化模型失去意义。因此，在进行多目标模型转化、单目标模型求解时应进行规范化处理。

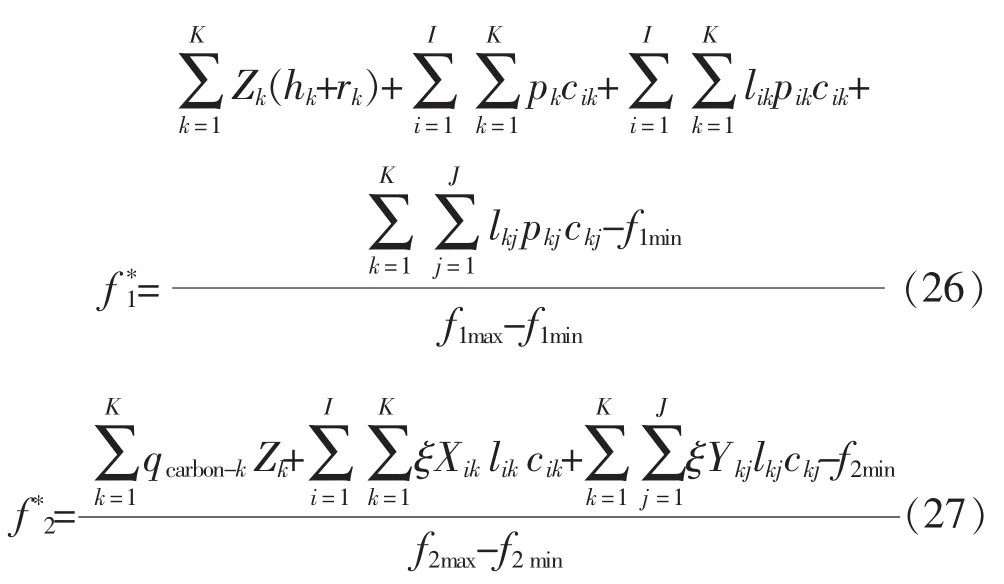
4.4.2 多目标模型转化单目标模型

电网物资配送中心多目标优化模型中的目标函数分别为配送中心选址总成本的最小化、物资配送中心的低碳配送排放量的最小化，以及配送中心备选地址综合评价得分的最大化。通过对目标函数无量纲处理，运用权重和法将多目标问题转化为单目标最小化问题。为此，本节采用较为直接的主观赋权法，通过决策者的偏好度进行权重赋值，即转化后的单目标函数为

式中：θ1，θ2和 θ3分别为决策者对第 1、第 2、第 3 个目标函数的权重偏好，且有 θ1+θ2+θ3=1。

4.4.3 NSGA-II算法求解分析

本文采用运行速度更快、解集收敛性更好的NSGA-II算法、基于Pareto支配关系进行计算求解结果如图1所示。

由图1可知，电网物资配送中心选址优化决策模型的选址地点呈离散变动的形态，空间中的点是在已知限定条件下的多目标优化模型的非劣解。随着种群规模的增加，非劣解集合的覆盖程度逐渐增大，稳定性也逐渐增强，优质解流失的概率越小，越趋于一个平稳的状态。

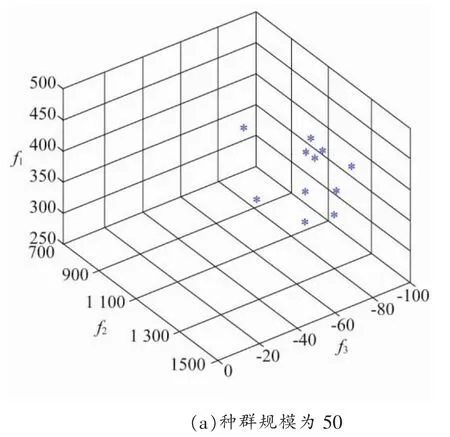
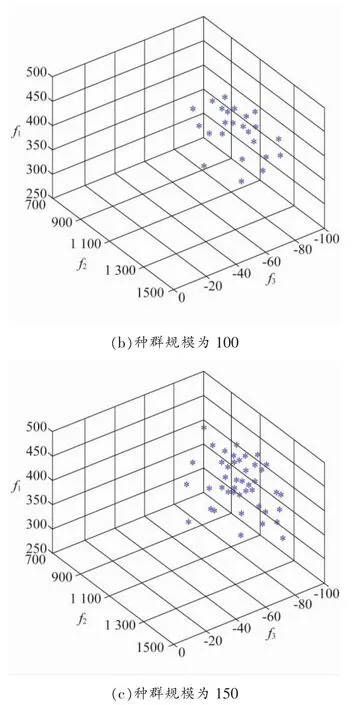
图1 NSGA-Ⅱ迭代300次运行结果

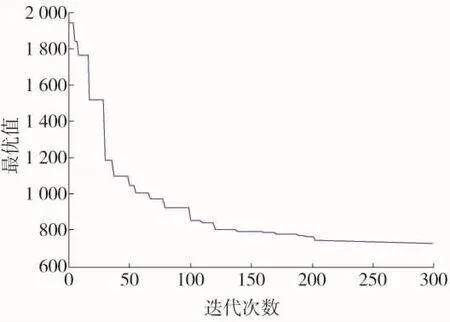
图2 多目标下NSGA-Ⅱ算法迭代优化

对比图1（a）～（c）后可以发现，随着种群规模的不断增加，多目标优化模型的可行解数量逐渐增多，最后趋于一致。换句话说，在种群规模较小的情况下得到的可行解的数量和质量低于种群规模较大时可行解的数量和质量。但是初始种群规模太大将导致计算量增加，也降低了NSGA-Ⅱ算法的计算速度。因此，由于设置的种群数量较多，决策者进行决策时可根据实际情况的需要，本文种群规模N=120。

4.4.4 结果分析

θ1，θ2和 θ3权重的取值直接影响多目标优化模型的Pareto最优解，为研究不同目标函数对电网物资配送中心选址方案产生的影响，本节设定5组不同的θ1，θ2和θ3权重系数值，计算求出不同权重值下的配送中心选址分配方案及各目标函数值，结果如表5所示。

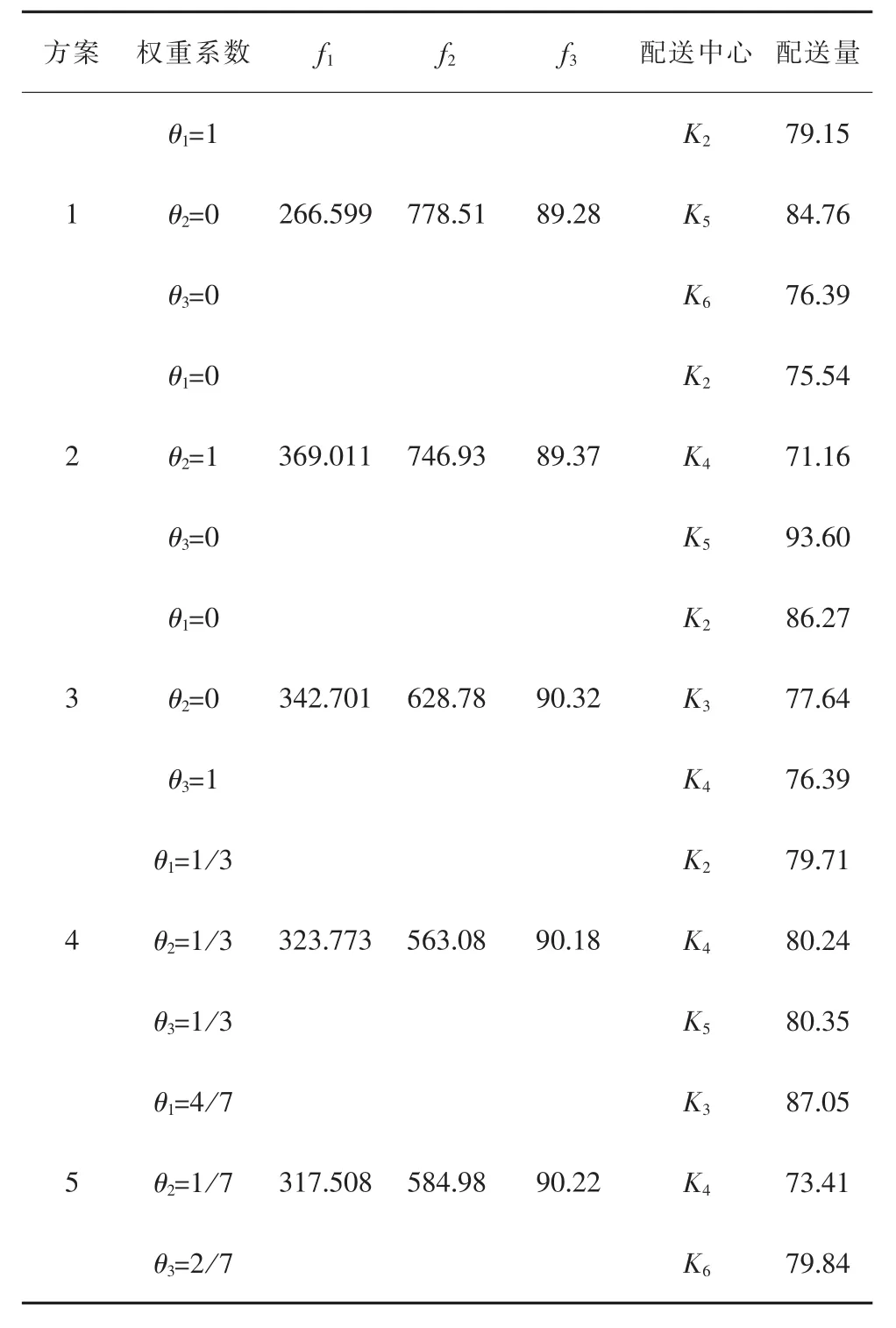
表5 不同权重系数下多目标优化的选址方案

在多目标优化（即权重系数为 θ1=4/7，θ2＝1/7 和θ3＝2/7）的情况下，电网物资配送中心的选址方案为K3，K4和 K6，此时的配送中心选址的总成本为317.508万元，低碳配送排放量为584.98吨，综合评价得分值为90.22。该配送中心选址方案下，K3，K4和K6的配送量较为均衡，配送方案和路线均得到了一定程度的优化，且各目标函数值都得到了相对程度的调和。

通常，在实际的电网物资配送中心选址应用中，决策者根据自己的权重偏重，改变权重系数θ得到满意的选址方案。此外，针对θ进行不同的权重赋值，可以求得组成电网物资配送中心选址的Pareto最优解集合。

各选址方案下配送中心配送量分配情况如表6所示，选址方案4的配送路径拓扑如图3所示。

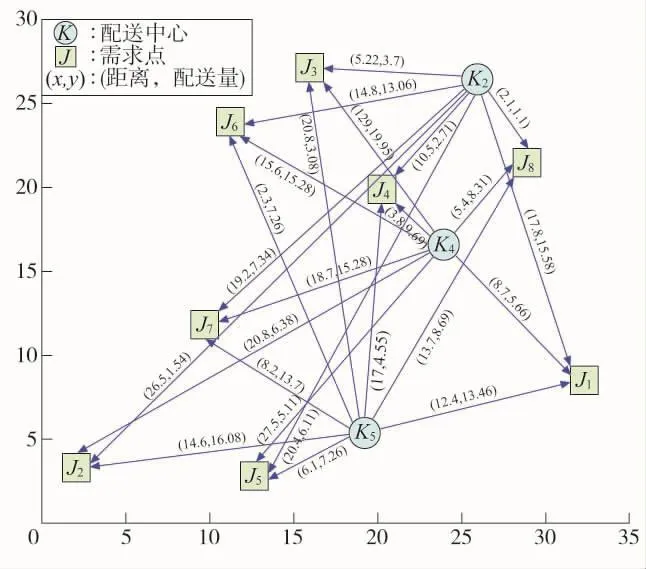
图3 选址方案4的选址方案及配送路径拓扑

实际上，多目标优化下的配送中心选址方案比仅考虑选址总成本目标下的选址方案在成本费用方面有所增加，但配送中心的低碳配送排放量和综合评价得分值方面得到了提升和优化，也证明了多目标优化模型中这两个目标函数的价值和意义。此外，综合评价评分值参数作为各备选配送中心选址多目标优化模型中的一个目标函数，它是独立的参数，与多目标优化模型中的其他量化约束、目标并没有直接的联系，表示备选配送中心在定性评价过程中的优劣性和适合建址的程度。综合评价评分值的目标与总成本费用目标、低碳配送排放量目标之间具有相对的独立性，但会对最终的选址方案产生影响，不同的评价值组合会产生不同影响，且都能得出类似的结论。

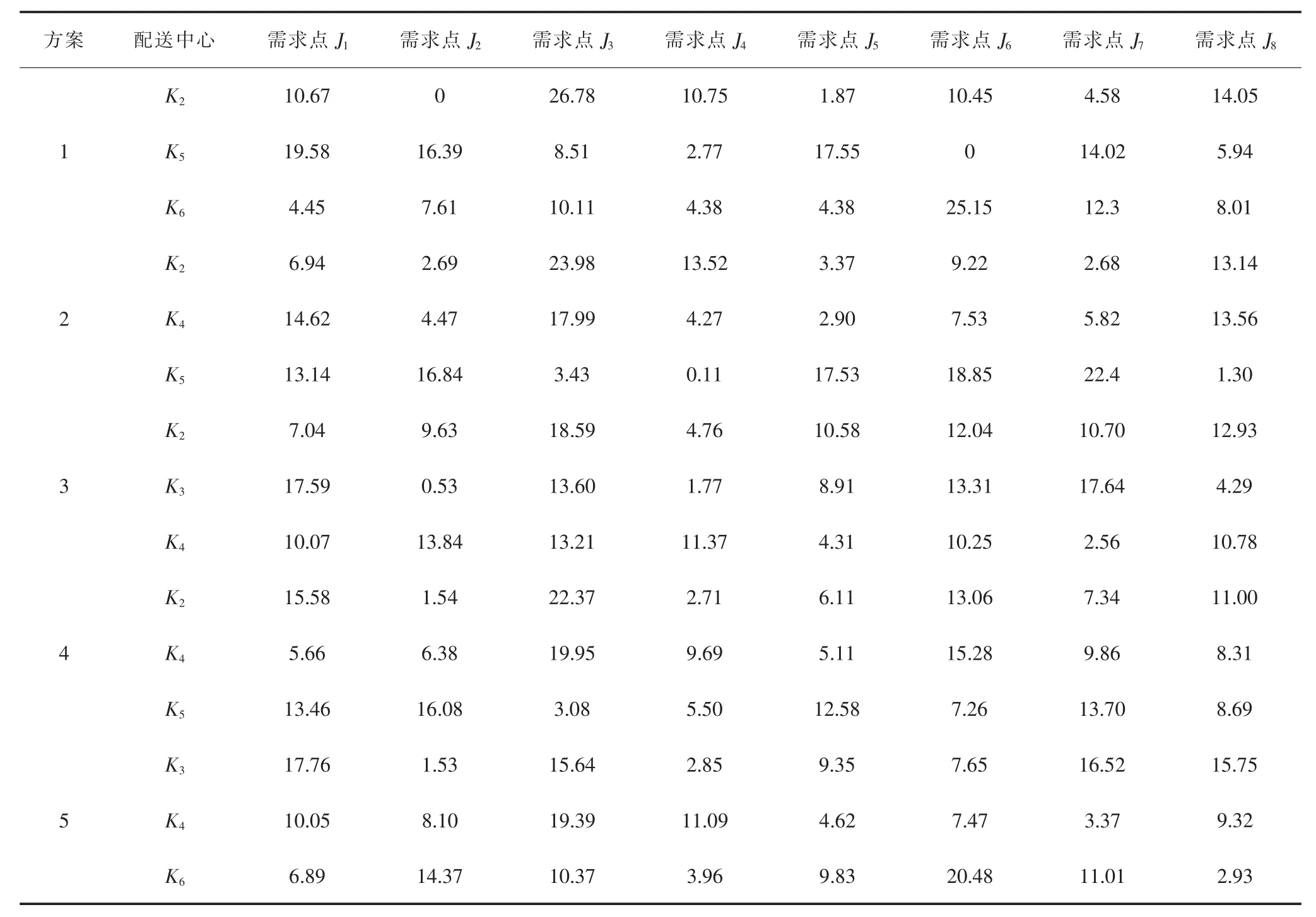
表6 各选址方案下配送中心配送量分配情况

5 结语

对电网物资配送中心的选址进行科学、合理地规划，是提高物流管理水平与资源利用率、降低运行成本、提升企业管理水平的关键举措。在综合考虑配送中心选址影响因素的基础上，提出并建立配送中心选址多层次维度的评价指标体系；其次，基于IAHP-COWA法组合赋权优化，构建基于FCE的配送中心选址优化模型，对候选地址进行打分评价。将综合评分值作为目标函数之一，建立电网物资配送中心选址多目标优化模型，基于NSGA-Ⅱ算法求解多目标函数，确定最终的中心设施地址和配送方案，为省级电力公司降低配送成本、提升配送效率、提高电网物资集约化水平提供决策依据。