逢山开路 遇水搭桥——解析几何问题中参数的选择策略

□王 炜

（江阴市华士高级中学，江苏江阴 214421）

解析几何是用代数方法研究几何对象之间的关系和性质的一门几何学分支.研究问题时，需要将几何问题转化为代数问题，然后在代数中研究几何问题.如果难以直接寻找x与y之间的关系，怎样将几何问题代数化？往往要引进参数，再通过消参解决问题.如何引进参数？常言道：逢山开路，遇水搭桥.何时“开路”？何时“搭桥”？涉及参数的选择.在教学中，笔者通过预判性的几何问题代数化策略来选择参数.

一、问题提出

题目：在平面直角坐标系xOy中，已知圆C的方程为x2+(y-1)2=5，点A为圆C与x轴负半轴的交点，过A作圆C的弦AB，记线段AB的中点为M.若OA=OM，求直线AB的斜率.

此题是南京市、盐城市2015届高三年级第二次模拟考试填空题的第12题，属于中档题.具体解答如下.

法 1：设直线lAB：y=k(x+2)，再与x2+(y-1)2=5联立方程组，消去y得x1+x2=，则即，由OA=OM=2，得k=2(k=-2舍去）.

法2：设点M(x0，y0)，则B(2x0+2，2y0)，由OM=2得x02+y02=4①.再将点B代入圆C，得：x02+(y0-1)2=5②.由①②得：y0=2x0+4，则

提出问题：该题设点、设线均可，我们知道“点在线上，且线经过点”，何时设点？何时设线？

二、问题梳理

解析几何问题求解一般有三个环节：设参、转化、消参.作为第一环节的设参是否合理，对后续的运算有较大的影响.实践中不少学生因为设参不合理，导致运算量偏大而不得不中途放弃.设点、设线是解析几何中两种重要的设参方法.在平时的解题教学中，教师要努力引导学生选择不同的参数，尝试不同的路径解题.这样既可以训练思维的发散性，又可以训练思维的收敛性（即优化思维），从而发展学生的数学核心素养.

图1是解析几何求解的思维导图.

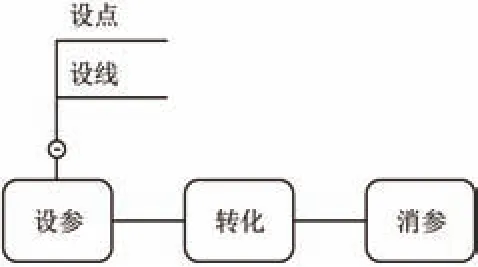
图1

【名词解释】

点相关：两个点的横坐标或纵坐标之间有明显关系称之为“点相关”.例如：已知P，Q两点关于原点对称，则点P与点Q对应的横、纵坐标互为相反数，即点P( )x，y，则Q（-x，-y），所以称P，Q两点为“点相关”.

线相关：斜率相关（两直线斜率相等或相反数等），或能够将问题转化为两根之和（或之积），称之为“线相关”.例如：已知两直线OP，OQ互相垂直且两直线的斜率都存在，设直线OP的方程为y=kx，则直线OQ的方程为所以称两直线OP，OQ为“线相关”.

该题为什么既可以设点，又可以设线？“点相关”“线相关”梳理如表1.

表1

图2是“点相关”与“线相关”的思维导图.

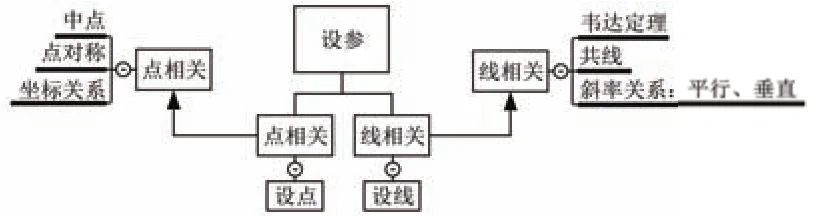
图2

设点、设线有什么不同之处？问题梳理如表2.

表2

从参数的个数上来看，设线简单些；从代入曲线上来看，设点代入简单些.仅仅据此分析，该题的这两种设参的方法不分高下.考虑到条件“OM=2”，则设点比设线来得更直接，所以第一思维是设点.以后处理这类既“点相关”又“线相关”问题时，需进行两方面的分析：①已知分析：已知中哪一种相关性更大些，或者说哪一种设参能将已知中的几何关系更恰当地用代数方法表达出来；②所求分析：哪一种设参能更有效地联通已知与所求.

三、问题突破

（一）若点相关，选择设点

例1如图3，已知M，N是椭圆上关于原点O对称的两点，点P是椭圆C上的动点，且直线PM、直线PN的斜率均存在.问kPM⋅kPN是否为定值，并说明理由.

图3

【路径1】设点M(x，y)，则点N(-x，-y)，求得kPM⋅kPN为定值.

【路径2】设直线lMN：y=kx，讨论直线MN的斜率是否存在，求得kPM⋅kPN为定值.

【总结提升】设线不仅需要对直线MN的斜率是否存在进行讨论，而且需要将直线MN与椭圆C联立方程组求解.比较这两种设参的方法，明显“设线”不合理.“点相关”的理由有两条：理由1，M，N是椭圆C上关于原点O对称的两点；理由2，研究的对象是kPM⋅kPN，而点P是椭圆C上的动点，需要用到斜率的坐标公式.

（二）若线相关，选择设线

例2已知圆O：x2+y2=25是△ABC的外接圆，点A的坐标为( )3，4 ，且直线AB与直线AC的倾斜角互补.求证：直线BC的斜率为定值.

【分析】因为直线AB与直线AC的倾斜角互补，所以直线AB与直线AC的斜率互为相反数，它们具有“线相关”，所以考虑设线.

例3（由山东2009年高考题改编）如图4，过原点O作两条互相垂直的射线，与椭圆交于A，B两点.证明：原点O到直线AB的距离为定值.

图4

【路径1】设直线AB的方程为y=kx+m，讨论直线AB的斜率是否存在.

【路径2】设直线AB的方程为x=ty+n，讨论直线AB的斜率是否为0.

【路径3】设直线OA方程为y=kx，讨论直线OA的斜率是否存在、是否为0.

【总结提升】设线有三条路径，如何选择？选择路径3.理由：第一，OA⊥OB；第二，引进的参数最少；第三，从计算量看，直线OA与椭圆联立方程组明显小于直线AB与椭圆联立方程组；第四，求得OA的长度，这样同理可得OB的长度，从而减少运算量.

（三）路径预判，优化设参

例4如图5，在平面直角坐标系xOy中，已知椭圆的左、右顶点分别为A、B，且点C的坐标为( )1，0.圆O：x2+y2=4上有一动点P（P在x轴上方），直线PA与椭圆E的另一交点为点D，连结PB，DC.设PB，DC的斜率存在且分别为k1，k2，若k1=λk2，求λ的取值范围．

图5

【动态分析】运动元素：动点有点P，点D；动线有直线PB，直线DC，直线PA.

路径预判：

【路径1】设线lPB→表示lPA→联立求点D（已知一交点）→表示k2→求λ范围.

【路径2】设线lCD→联立求点D（运算量大）→表示kAD→表示k1→求λ范围.

【路径3】设线lPA→表示k1，联立求点D（已知一交点）→表示k2→求λ范围.

【路径4】设点P( )x0，y0→表示k1，表示lPA→联立求点D→表示k2→求λ范围.

【路径5】设点D( )x0，y0→表示kPA，表示k2→表示k1→求λ范围.

【反思提升】根据运算量的大小，将这五种解法按照运算量由小到大进行排序：路径5，路径1或3或4，路径2.

学生的实际情况：①设线的学生倾向于路径3，设直线lPA：y=k( )x+2；②设点的学生倾向于路径4，设点P(x0，y0).说明学生参数选择时，还是带有盲目性，缺乏理性思考.如何理性思考？选择参数时，要对问题进行动态分析并挖掘几何特征，因为AB是圆O的直径，则PA⊥PB，所以直线PA、直线PB的斜率之间互为倒数的相反数.分析可知核心运动元素是点D.核心运动元素即牵一发而动全身的点或线，并且这个运动元素能更合理地表达问题中的几何关系，从而有效地联通已知和所求.

四、问题解决

知识可分为三类：陈述性知识、程序性知识和策略性知识.知识的获得可用四象限学习特征所示（见图6）.

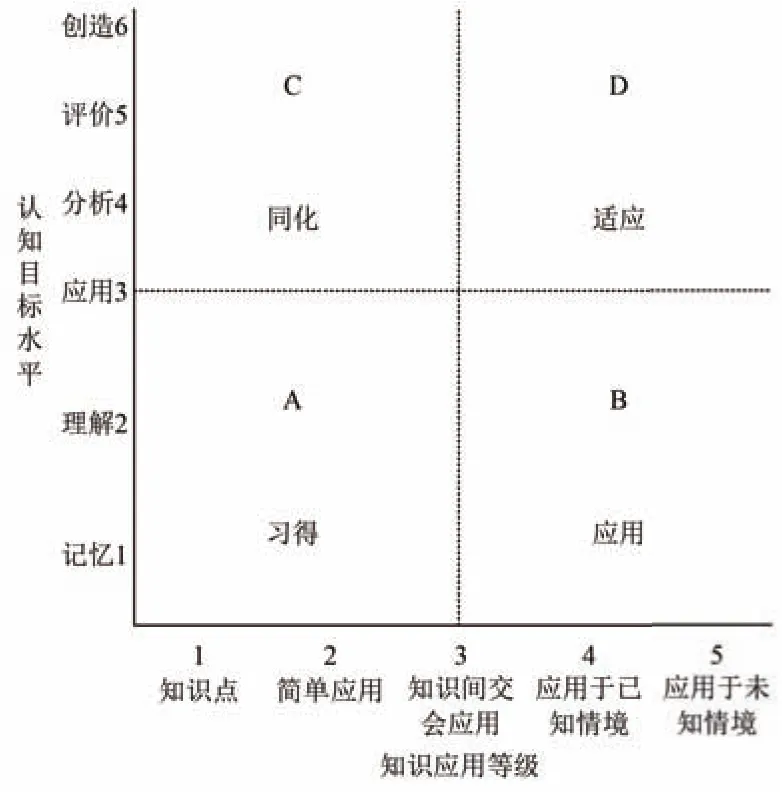
图6

本文所研究的“解析几何问题中参数选择策略”是策略性知识.策略性知识是指学习者在学习情境中对任务的认识、对学习方法的选择和对学习过程的调控，它是由学习方法、学习调控和元认知等要素构成的监控系统.所以策略性知识仅靠习得是无法获取的，它需要在分析中比较，在评价中优化，在创造中创新.

解析几何中参数选择的策略是：预判性的几何问题代数化.通俗地讲就是：逢山开路，看路在何方；遇水搭桥，知桥通何处.参数选择这一策略性知识的获取途径有：①在日常教学中教师要加强引进不同参数的比较，②在教学设计中教师关注参数选择的预设和生成，③教师调动学生参数选择的主动性.对“参数选择策略”的研究，可促使学生自觉养成用数学的眼光发现和提出问题，用数学的思维分析和解决问题，用数学的语言表达和交流问题的习惯.教师务必培养学生自己“找路”（即参数选择）的能力，让学生自己做“司机”，而不是始终做“乘客”.在这一过程中，教师要做一个隐形的“指路人”：在直路上，大胆让学生独立操作；在岔路口，引导学生看路标；在迷路时，给予必要的点拨.

策略性知识的获取并非一蹴而就，是一项长期的工作.在这项工作中可进行一些探究式教学，激发学生学习数学的兴趣，引导学生进行参数选择分析：点线相关分析、路径预判分析，多一些理性的思考，少一些运算，是进一步优化数学思维品质，发展数学核心素养的有效途径 .