光伏并网逆变器控制策略研究
2019-07-03廖碧莲唐江琦吴誉寰高中林
廖碧莲,唐江琦,吴誉寰,高中林
(广西大学电气工程学院,广西 南宁 530004)
0 引言
分布式发电目前以独立运行和联网运行两种运行模式为主。为了更加高效地利用能源,目前的趋势是将分布式电源与电网结合在一起联网运行,两者相结合,可做到取长补短,达到提高电力系统安全性、可靠性和灵活性的目的[1]。因此,作为分布式电源和电网相联的主要装置,并网逆变器显得格外重要。
分布式电源要求所使用的并网逆变器需具备高效、低成本的特点,且能适应实际运行中可能出现的直流电压波动大或电压低等现象。另外,逆变器的输出要有较高的电能质量,在频率、电压和波形畸变率等方面满足相关的要求[2]。
大功率系统中的传统逆变器在使用时往往需要和一个笨重的工频变压器配合,以确保对逆变过程中产生的谐波、直流分量做到有效隔离,从而满足技术标准和规范对并网设备的要求,但该方案有其固有的缺点,例如成本高、体积大、重量重,尤其工频变压器的存在使得进一步提高逆变效率变得非常困难[3]。当今电力电子“多硅少铁”的技术趋势不可阻挡,而传统逆变器并不符合“多硅少铁”的技术特点,目前对并网逆变器的研究主要集中在缩小占地面积、降低使用和维护成本、全面提高转换效率、增强承受直流电压波动的能力等方面。
逆变器的调制方式主要分为方波、阶梯波和正弦波脉冲宽度调制(sinusoidal pulse width modulation,SPWM)。方波逆变器的输出电压波形为方波,其特点是线路简洁、价格低廉、功能实现容易[4]。不过其缺点在于输出的方波电压中含有大量高次谐波成分,会产生附加损耗,同时高次谐波也会对通信产生干扰,所以一般只用在小容量逆变器中。阶梯波逆变器的输出电压为阶梯波,输出的波形类似于正弦波,含有的高次谐波成分较少,但其缺点在于需要多组直流电源供电,需要的功率开关管较多。SPWM逆变器的输出波形基本为正弦波,产生谐波损耗非常少,效率较高。脉宽调制(pulse width modulation,PWM)型逆变器的开关管大多使用绝缘栅双极性晶体管(insulated gate bipolar transistor,IGBT)、可关断晶闸管(gate turn-off thyristor,GTO)等器件,控制部分通常为PWM集成电路以及带有PWM输出的数字信号处理(digital signal processing,DSP)和单片机芯片。

图1 三相并网逆变器控制系统的典型结构Fig.1 Typical structure of three-phase grid-connected inverter control system
逆变器主要分为两种:电压型逆变器和电流型逆变器,本文采用电压型逆变器。本文将分布式电源等效为直流电压源,采用双闭环控制策略作为逆变器的控制方式,外环控制方法通常为恒功率(PQ)控制和恒压恒频(VF)控制,内环通过对三相瞬时电流或电压进行派克变换,将其转换至dq旋转坐标下实现两相控制,从而简化了分析计算[5-6]。
1 电压型三相并网逆变器的典型结构
图1为电压型三相并网逆变器控制系统的典型结构[7]。
图1中的等效直流电源经SPWM控制的三相并网逆变器逆变后转化为交流电,再经LC滤波器滤波后输送至交流网络中。图中:L是滤波电感,C是滤波电容,uIabc是逆变桥输出电压,iIabc是滤波电感上流过的电流,uGabc是逆变器输出电压。
根据图1可列写如下电路微分方程式:
2 逆变器的控制方程
方程(1)、(2)为变系数微分方程,直接求解较为复杂,可通过派克变换将两方程的三相正弦量转换为同步dq旋转坐标系里的直流变量。由三相abc坐标系转换到两相dq坐标系所使用的变换矩阵如下:
(3)
式中θ为同步旋转dq坐标系下q轴与电网a相之间的夹角。
对式(1)和(2)进行正交派克变换可得
由式(4)可知,d、q轴电感电流不仅与-uGd、-uGq有关而且和电流交叉耦合项ωLiIq、-ωLiId有关。故引入电网电压前馈补偿uGd、uGq和电流交叉耦合补偿-ωLiIq、ωLiId,有
(6)
式中:kp为比例增益;ki为积分增益。
同理可引入电网电流前馈iGd、iGq和交叉耦合补偿-ωCuGq、ωCuGd,有
(7)
将式(6)、(7)代入式(4)、(5),可得解耦的电流内环和电压外环控制方程如下:
3 逆变器的控制策略
3.1 外环控制
外环控制模式为恒功率控制,该控制策略的特点是当逆变器所接交流网络的频率和电压额定值在允许范围内变化时,分布式电源输出的有功和无功功率保持不变。对于光伏发电、风力发电这类具有间歇性、功率波动比较大的分布式电源,恒功率控制特别合适[8-9]。根据三相瞬时无功功率理论,可将并网逆变器输出的有功功率P和无功功率Q以dq坐标系的模式表示为
(10)
假设三相电网电压是理想正弦波,则三相电压在abc三相静止坐标系下可表示为
(11)
式中:Um为电网电压峰值;ω为基波角频率。将式(11)通过式(3)进行派克变换的uGd=Um、uGq=0。则式(10)可表示为
(12)
由式(12)知,三相逆变器输出有功功率可通过d轴电流调节,无功功率可通过q轴电流调节[10]。恒功率控制原理如图2所示。
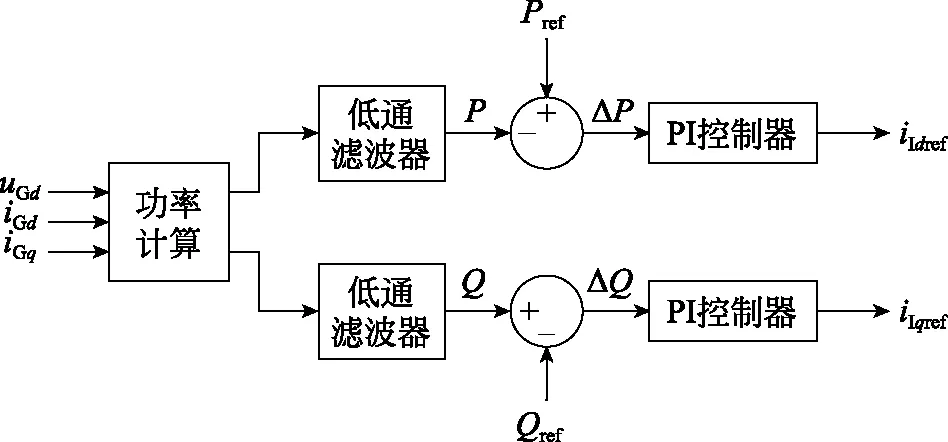
图2 恒功率控制原理图Fig.2 Constant power control schematic
如图2所示:经过dq变换后的网侧三相电压电流转换为uGd、uGq、iGd、iGq;经过功率计算器和低通滤波器后可得到网侧平均有功功率P和平均无功功率Q;将网侧有功功率P和无功功率Q与参考有功功率Pref和参考无功功率Qref比较后的差值传入至PI控制器当中,经过PI控制器的跟踪处理后输出的信号为内环控制参考电流信号iIdref、iIqref,再将参考电流信号输入内环控制器当中,从而完成对输出有功和无功功率的控制。

图4 逆变器主电路Fig.4 Main circuit of inverter
3.2 内环控制
内环控制是利用派克变换将网侧三相瞬时电流或电压转换到dq坐标系下,从而将三相控制变成两相控制,达到简化计算、降低分析难度的目的[11-12]。本文内环控制选择对网侧三相瞬时电流进行派克变换,再根据式(4)设计的内环控制结构如图3所示。
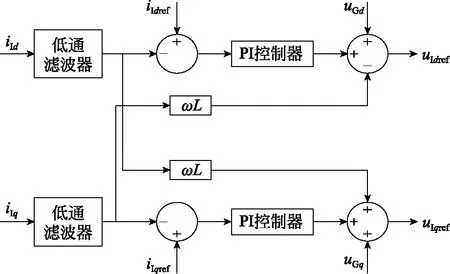
图3 内环控制结构图Fig.3 Inner loop control structure
将经过派克变换的网侧三相瞬时电流iId和iIq,与外环控制器得出的参考电流iIdref、iIqref比较后,送入PI控制器中,再与电网电压前馈补偿uGd、uGq和电流交叉耦合补偿-ωLiIq、ωLiId比较,得出电压控制信号uIdref、uIqref;将该控制信号送入PWM调制器中,经过三角载波调制发出触发脉冲序列给逆变器,完成整个控制过程[13-14]。
4 仿真和实验结果分析
根据制定好的逆变器控制策略,在PSCAD软件中搭建仿真模型[15-16]。逆变器主电路如图4所示,其中直流电压Ed=800 V,滤波器选用LC滤波器,L=6 mH,C=4 μF。
仿真模型的Pref和Qref分别设置为100 kW和60 kvar,仿真时间设为1 s,逆变器的输出波形如图5所示。
由图5可看到在双闭环控制策略下逆变器的有功无功和网侧电压电流。为进一步验证其有效性,在PSCAD软件中搭建小型微网系统,主电网为理想的无穷大电源,微电网的初始负荷有功功率为100 kW,无功功率为100 kvar,在0.6 s时系统接入一个有功功率为100 kW、无功功率为20 kvar的新增负荷,仿真时间设为1 s,结果如图6所示。
由图6可知,当系统所接负荷增加时,逆变器输出的有功无功未发生改变,所增加的负荷由主电网提供,系统的母线额定电压保持不变。通过仿真验证了该控制模型的正确性。
5 结论
本文提出的分布式电源并网逆变器的控制策略主要包含两方面:外环控制策略和内环控制策略。外环控制策略为恒功率(PQ)控制,通过对网侧dq轴电流的调节可控制逆变器输出的有功和无功功率;内环控制是将网侧电流进行派克变换后与外环控制送来的参考电流比较、补偿后产生PWM控制信号,从而完成整个闭环控制过程。同时,本文还在PSCAD/EMTDC软件中仿真,进一步验证了控制策略的有效性,仿真结果符合预期。
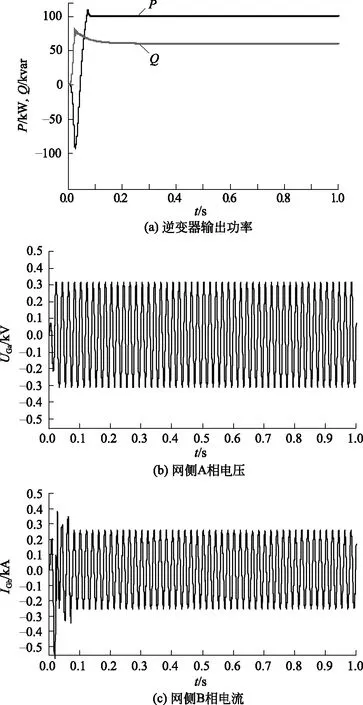
图5 逆变器的输出波形Fig.5 Inverter output waveform

图6 系统有效性验证Fig.6 System validity verification
