解读条件与成果扩大：较难题的教学关键

☉江苏省张家港外国语学校 周桂荣

进入中考复习之后，每份综合试卷都会有2～3道较难题用来承担区分选拔功能，这些较难题往往因为小问之间的梯度拉开较大，学生在较短时间内不能获得思路，或者苦恼于无思路，待到讲评时教师一讲又觉得特别简单，往往发出“考试时我怎么就没有想到这个思路呢”的感叹.本文结合最近一次较难题的教学案例，谈谈在较难题教学过程中要注意引导学生解读条件并促进学生成果扩大，以便自主发现较难题的求解思路.

一、较难题的教学案例

（1）AP⊥BC时，求运动时间t.

（2）在运动过程中，是否存某一时刻，使得△APQ为直角三角形？如果存在，求出t的值.

（3）当t＞6时，记△APQ的面积为S，求S与t的关系式.

图1

图2

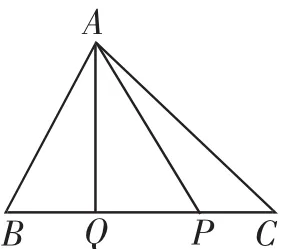
图3

图4

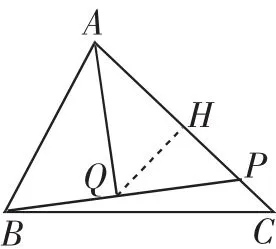
图5

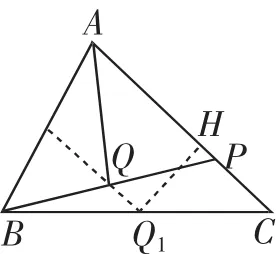
图6

讲评记录：第（1）问比较简单，如图2，只是让学生初步感受过点A作BC边上的高AP，并熟悉该图形中一些重要数据，比如，△ABP三边之比是1∶2∶，△APC三边之比是1∶1∶，学生对这个小问都能顺利解决.

第（2）问第一种情况就是在图2的基础上，画出BC边上的高AQ，PQ=BQ，这就是符合要求的一种情况.但是当点P运动到AC边上时，有学生构图时就出现了困难.笔者安排学生上台先在AC上任取一点P，连接BP，并取中点Q，不断调整构造出如图4这样的相对精准的图形，这时大家就发现了△ABP是特殊三角形（等腰三角形），从而就容易求出AP的长，于是运动时间就确定了.

对于第（3）问，学生的主要障碍在AP边上的高QH无法用含t的式子表示.这时我们引导学生反复读题，深入思考“动中点”Q的运动轨迹，学生发现了如图6这样的情况，于是想清了AP边上的高一定等于Q1H，进一步利用直角三角形Q1HC中的边角关系.由CQ1=3，就可求出Q1H的长为

教后反思：教学过程中，在第（2）问求解出现困难时，安排学生构造草图、反复调整，这是对题目条件的深入理解、精准构图的需要；而对于第（3）问，当学生出现困难时，我们没有直接告知思路，只是启发他们退回条件进行分析，想清Q点的运动轨迹（也就是促进学生追求“成果扩大”，丰富对中点Q的信息解读），这样对于发现AP边上的高是不变的很有帮助.

考题2：已知正方形ABCD，点A（0，-4）、B（1，-4）、C（1，-5）、D（0，-5），抛物线y=x2+mx-2m-4（m为常数）的顶点为M.

（1）小海发现抛物线会经过一个定点，请分析小海的发现是否正确，并说明理由；

（2）求顶点M的坐标（用含m的代数式表示）；

（3）若抛物线y=x2+mx-2m-4（m为常数）与正方形ABCD的边有交点，求m的取值范围.

讲评记录：（1）抛物线y=x2+mx-2m-4改写为y=（x-2）m+x2-4，于是可确认x=2时，y的值为0，与m无关，即抛物线经过定点（2，0）.

（3）对于这一问，不少学生表示没有思路，追问他们原因，发现多数学生感觉抛物线是运动的，无法画出草图分析.于是先引导学生分析前两问，进行成果扩大.首先，抛物线会经过定点（2，0），进一步，顶点坐标说明顶点的运动轨迹是什么？学生经过分析，取x=-，y=-m2-2m-4，则m=-2x，代入后得y=-x2+4x-4，确认了顶点在抛物线y=-（x-2）2上运动.在此基础上，可以画出草图7分析，从而确认抛物线在运动变换过程中与正方形ABCD的两次临界相交情况（顶点在点A处，抛物线经过点C）.把点A（0，-4）的坐标代入y=x2+mx-2m-4，解得m=0；把点C（1，-5）的坐标代入y=x2+mx-2m-4，解得m=2.所以0≤m≤2.

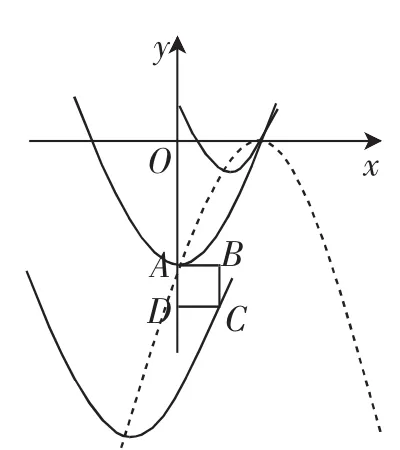
图7

教后反思：较难题的解题思路难以打开时，往往是因为前后问题之间的“落差”较大，学生缺少必要的铺垫式问题来“过渡”，这也启发我们在解题教学中，要善于预设铺垫式问题，通过启发式讲授帮助学生顺利地获得思路，提高解题教学效率，也促进学生学会解题.

考题3：如图8，⊙O的直径AB=26，P是AB上（不与点A、B重合）任一点，C、D为⊙O上两点.若∠APD=∠BPC，则称∠CPD为直径AB的“回旋角”.

（1）若∠BPC=∠DPC=60°，求证：∠CPD是直径AB的“回旋角”.

图8

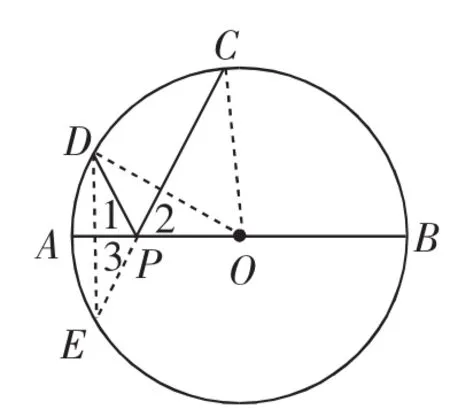
图9

教学记录：（1）证明的关键是计算出∠APD=∠BPC=60°.于是∠CPD是直径AB的“回旋角”.

（2）这一问对学生来说有些困难，这时启发他们补全同形，如图9，延长CP，交⊙O于点E，连接DE、OD、OC.由的长为π，r=13，可得圆心角∠DOC=45°.接下来引导学生思考同弧所对的圆心角与同弧所对的“回旋角”有怎样的关系.学生在图9中推理，如下所示：

∠2=∠3，∠1=∠2，可得∠1=∠3. 由于点D、E关于AB对称，所以PD=PE.于是∠DPC=2∠E.结合∠DOC=2∠E，得“回旋角”与圆心角相等，即∠DPC=∠DOC=45°.

教后反思：当学生思维受阻时，教师需要预设恰当的启发式问题，这些提示语既不能直接告知答案，也不能与答案的距离“过近”，需要设计一些“跳一跳，够得到”的思路启示或铺垫式问题，让学生继续挑战、接通思路.

二、关于较难题解题教学的几点思考

1.教师要对较难题关键解题步骤有准确研判

较难题的讲评往往会占去很多课堂教学时间，有时讲评之后效果并不理想，因为讲评时重点不够突出，难点突破没有得到充分展示，所以学生对难点、易错点、关键步骤没有达到深刻理解.这就需要教师在课前解答较难题时不能只是满足于解题思路的贯通、答案的获得，而且要善于解后反思，想清辨明这道较难题的关键步骤是哪一步或哪几步，难点在哪儿，易错点、易混点在哪儿，怎样体现“回到概念”去解题的解题理念，这样在讲评时才可能做到有的放矢、重点突出地讲评与引导.

2.解题教学之前要精心预设铺垫式问题

较难题的解题教学之前，教师要精心备课，特别是预设铺垫式问题，以便当学生思维受阻时能通过恰当的提问或启发，使学生“有路可循”，自主发现.铺垫式问题的设计要针对习题的难点或关键步骤，围绕题目条件或某些经典问题的结构进行.比如，上文“考题3”，当学生思路不通时，我们通过启发学生思考新定义“回旋角”与圆心角之间的关系，引领学生尝试证明它们相等，从而打开思路，这种铺垫式问题不但实现了解题目的，也是向学生传递会解题的思考方法，即当我们遇到一些较难题时，要善于“向后退”，退到条件再出发，反复解读条件中的信息，成果扩大后再迎难而上.

3.引导学生解后反思想清辨明关键步骤

较难题讲评之后，不少教师一般会安排一定的时间让学生整理过程，不然有些学生只顾听讲，似能理解，但记不下来过程，下课之后黑板擦了，很快又忘了.我们认为，不但要安排学生做适当的过程记录，还要引导学生进行解后反思，突出解题步骤中哪些是关键步骤，哪些是易错步骤，哪些是自己没有想到的一种解题念头，等等.要通过解题教学中渗透解后反思的教学环节，促进学生善于解后反思这一优秀习惯的养成.