梯度域和深度学习的图像运动模糊盲去除算法

郭业才, 郑慧颖， 叶 飞

(南京信息工程大学 a.江苏省大气环境与装备设计协同创新中心, b.电子与信息工程学院， 南京 210044)

0 引 言

在获取图像时，可能由于外界环境或成像设备等原因，使得图像存在不同程度的退化降质，如模糊、噪声等，这些退化降质的数字图像对人们的生产生活有着极大的影响。因此，去除模糊，得到清晰图像非常重要。现有的图像去模糊算法主要有:①利用自然图像的边缘先验信息恢复清晰边缘[1-7]。这些先验信息对图像去模糊是有效的，但需要解决非凸性问题。此外，优化方法和模糊核估计过程均很复杂，会导致计算成本较高。②运用深度学习网络实现图像去模糊[8-15]。目前，利用深度学习的方法实现图像去模糊，在去卷积的过程中会使图像过于平滑，导致图像的高频信息和图像纹理细节丢失，这样不仅花费时间较长，而且会导致图像的振铃效应更加明显。

本文针对现有图像去模糊方法的不足，提出一种基于梯度域和深度学习的图像运动模糊盲去除算法。该算法利用图像梯度域减少无关细节的影响，提高模糊核估计的鲁棒性。结果表明，该算法在有效保持边缘信息、显著减少振铃效应的同时，去模糊效果较好。

1 图像去模糊原理及方法

图像降质退化过程如图1所示。输入图像x，在模糊核k和噪声n影响下，得到模糊图像为

y=k[x]+n

(1)

图1 一般图像退化模型

图像盲去模糊即模糊核未知，需要从模糊图像y中获取清晰图像x和模糊核k。盲去模糊问题可以将求解出的模糊核转变为非盲去模糊问题，即

(2)

式中：⊗表示卷积操作；式中第1部分是数据保真项，利用L2范数进行约束；第2部分是先验正则约束项，它与原始清晰自然图像有关，λ是使约束项和数据保真项之间比例平衡的参数，正则项的选择与选取的图像先验有关。

图像盲反卷积问题的不适定性可以通过正则化方法解决，本文通过CNN的容错能力、并行处理能力和自学习能力，将CNN可以学习图像自身特征的性能用于去模糊的问题中，设计了一个有效的CNN网络结构。

2 图像运动模糊盲去除算法

2.1 图像预处理

首先，将引导滤波[16]后的图像作为基础图像，以减少噪声和多余细节的影响。然后，将L0滤波[5]后梯度域图像以及对应的清晰图像作为样本，对设计的CNN进行训练。本文中，引导滤波和L0滤波都是作用在清晰图像上的，可以抑制无关细节，增强图像的清晰边缘，提高了模糊核估计的鲁棒性。图2为图像预处理部分的结构流程图。

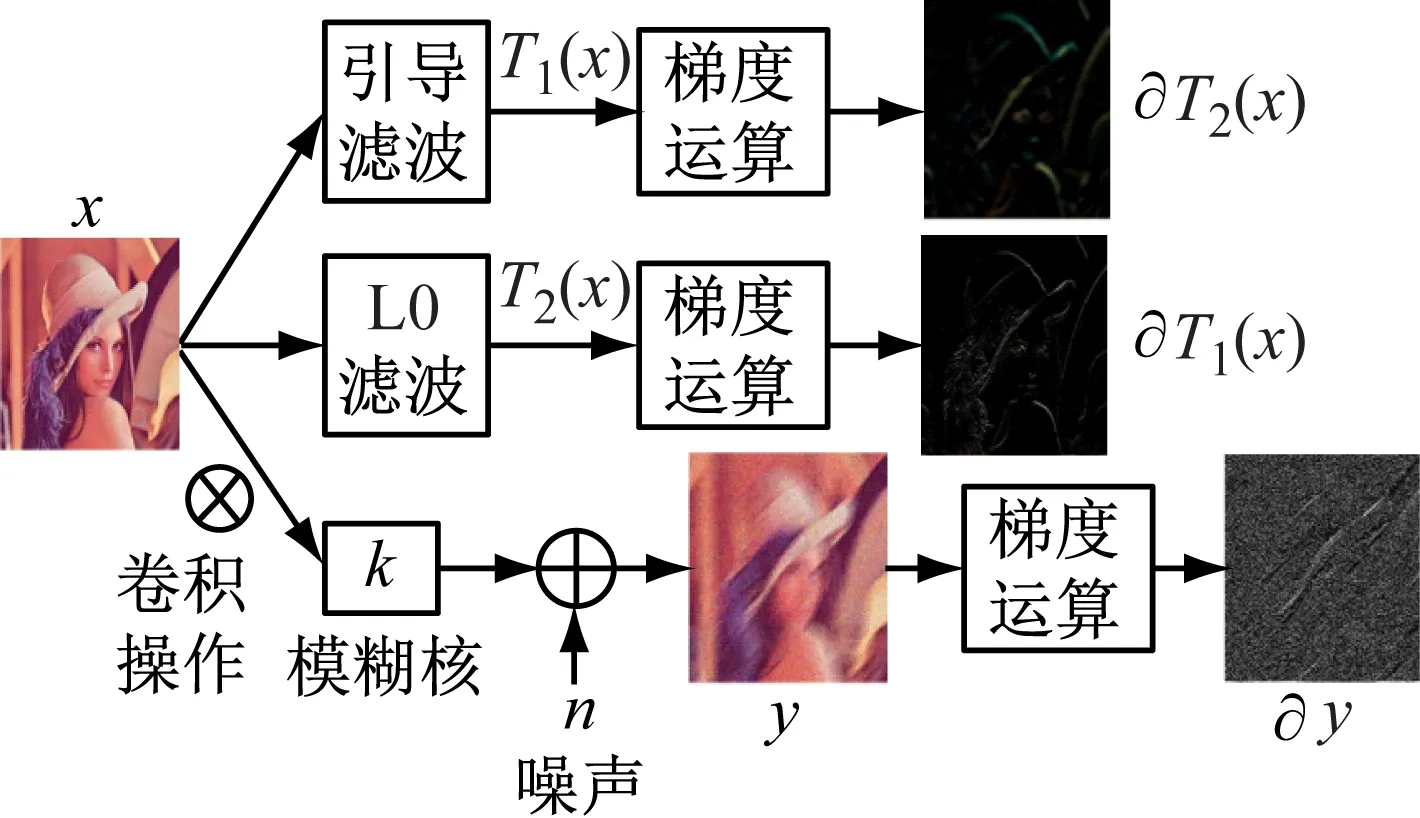
图2 图像预处理部分的结构流程

在利用滤波实现图像去模糊的基础上，提出利用引导滤波对图像进行预处理，因为通过引导滤波可抑制图像中的无关细节，并且保留图像的主要结构，如图3所示。其中，图3(a)是清晰图像；图3(b)是运动模糊噪声图像；图3(c)是清晰图像经过引导滤波后的图像；图3(d)是与清晰图像像对应的梯度域图像；图3(e)是模糊图梯度域图像；图3(f)是清晰图像经过引导滤波后的梯度域图像。

(a)(b)(c)(d)(e)(f)

图3 引导滤波处理结果图

2.2 卷积神经网络结构设计

文献[17]中提出利用梯度域图像训练CNN结构，而本文对文献[17]中的网络结构进行改进，提出利用较大卷积核提取图像的细节信息；加深网络层数使网络训练得到的权重数据更加准确。

现利用梯度域对网络进行训练。网络的输入分别经过引导滤波和L0滤波后的梯度域图像与其对应的模糊图像，输出为图像的边缘信息。把输入图片旋转90°后提取其边缘信息，与不旋转时提取边缘信息得到的效果相同，因此本方法仅利用垂直方向的梯度对网络进行训练，并在水平和垂直方向上共享权重，如图4所示。

图4 网络结构

由图4可得：

f0(∂y)=∂y

(2)

(3)

l=1,2,…,7

(4)

(5)

式中，{αm}是可学习的系数。

通过一组图像对D{∂yi,∂T1(xi)}，网络的第1阶段可以描述为问题：

(6)

式中：D表示真实图像和模糊图像的训练对；采用基于L1损失的TV正则化方法对图像梯度进行稀疏化处理；λ是正则化的权重。由于L1范数在0处不可微，因此利用Charbonnier函数，即ρ(z)=(z2+ε2)1/2来估计它。目标函数可写为

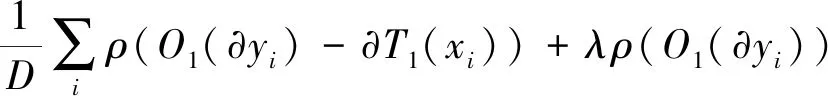
(7)

为了训练第2阶段的网络，最后3层的输出为:

(8)

(9)

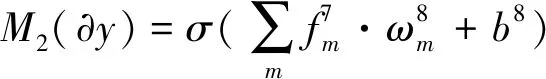
(10)

式中，gn是尺寸为q6×q6可学习的卷积核。

通过一组图像对D{∂yi,∂T2(xi)}，网络的第2阶段可以描述为问题：

(11)

两个子网络训练完后，将这两个子网络结合为

(12)

式中，m=1,2,…,p5；n=1,2,…,p6。

整个网络训练过程loss值为

(13)

式中：ρ(z)=(z2+ε2)1/2，ε取10-6；λ为正则项的权重；fω(∂yi)是网络训练得到的边缘信息。

2.3 图像去模糊

2.3.1 模糊核的估计

(14)

式中：参数η控制k的平滑度。第1项提供可靠边缘信息，第2项约束模糊核稀疏性，第3项

C(k)={(x,y)||∂xk(x,y)|+|∂yk(x,y)|≠0}

它的作用是使模糊核稀疏，也阻止出现不连续点，从而提高模糊核的连续性。

由于式(14)涉及到离散数值计算，因此很难直接对它求解最小值，本文将式(14)描述为：

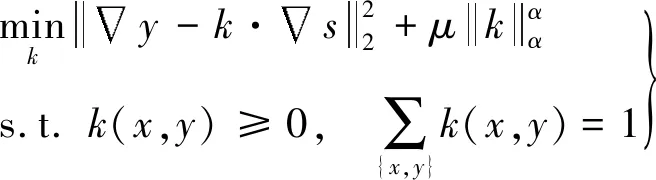
(15)

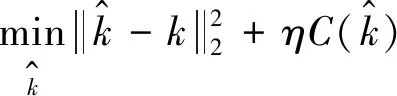
(16)

式(15)可以利用IRLS方法[19]求得，实验中，一共进行了3次迭代；式(16)可以通过交替优化[20]的方法求得解，一共进行了3次迭代。通过对上面两个子式的求解，最终可以得到模糊核k。

2.3.2 最终的潜像估计

得到模糊核后，最终潜像可通过非盲解卷积的方法获得。本文主要恢复运动模糊图像的边缘，采用TV正则化进行最终潜像的恢复，即

(17)

3 实验结果及分析

3.1 运动模糊图像生成

采用的图像数据库是BSDS500中的自然图像，为了获得模糊图像yi，对每一张清晰图像xi进行模糊处理。假设运动模糊是全局线性模糊，模糊核k=(l,o)受到长度和角度的影响。选取运动模糊的长度l从1～25，以2为间隔，角度o从0°～150°，以30°为间隔。由于当模糊核长度l=1时，不管运动方向是什么，所有的运动向量都对应着相同的模糊核，因此生成73个不同的模糊核。将这73个不同的模糊核与BSDS500中的500张自然图像xi进行随机卷积，再加上1%的高斯白噪声，就可以产生运动模糊图像。将产生的运动模糊图像裁剪成大小为45×45的模糊图像块，获得最终所需的模糊图像yi。本文通过给定模糊的图像yi，根据提出的方法首先计算垂直和水平方向的图像梯度，以梯度域图像作为卷积神经网络的输入。

3.2 网络结构

为了找到对图4所示结构作贡献的参数，进行了两组实验。两组实验中，CNN层数相同，每层滤波器数量不同，滤波器的大小不同。通过比较两组实验使用同一数据集在训练期间的loss值，来分析不同参数对实验结果的影响，如图5和图6所示。

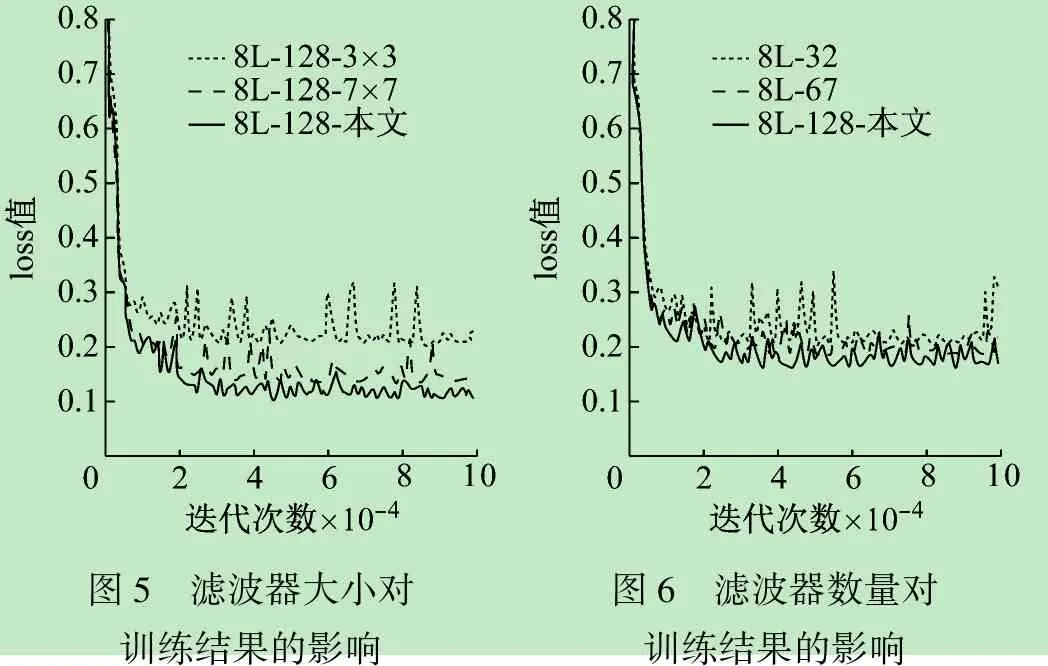
图5 滤波器大小对训练结果的影响图6 滤波器数量对训练结果的影响

训练整个模型一共进行10万次迭代，图5表示滤波器大小对训练结果的影响。整个网络一共8层，每层滤波器的个数均为128个。图中：紫色曲线是在大小不同的滤波器下获得的；蓝色曲线是在整个网络均使用5×5的滤波器下获得的；红色曲线是在整个网络均使用7×7的滤波器理获得的。图6表明，3种loss曲线约在85 000次时开始收敛，但本文方法采用不同大小滤波器时的loss值皆都低于其他两种情况。这表明，本文所选择的滤波器大小是合理的。

图6表示滤波器的数量对训练结果的影响。本实验的网络一共有8层，每层滤波器的大小均如图4所示，分别选取每层滤波器数量为64个和32个，与本文每层滤波器数量为128个进行对比。图中：紫色曲线是本文采用每层128个滤波器时获得的;蓝色曲线为网络每层使用64个滤波器时获得的，红色曲线为网络每层使用32个滤波器时获得的。图5表明，3种loss曲线大约在60 000次时开始收敛，但本文采用每层滤波器数量为128时的loss值均低于其他滤波器数量所对应的值。这表明，本文所选择的滤波器的数量是合理的。

3.3 去模糊效果

采用峰值信噪比(Peak Signal to Noise Ratio，PSNR)对去模糊的效果进行分析：

(18)

式中，T指图像像素强度的最大值。

去模糊效果分别与多层神经网络(Multi-layer Perceptron，MLP)方法[10]和边缘检测方法[21]进行对比。MLP方法利用多层感知器实现图像去模糊；边缘检测方法将图像结构与优化算法相结合应用于图像去模糊，如图7所示。

图7 去运动模糊效果

图7选取4张图像在不同模糊程度下，分别运用MLP方法、边缘检测方法及本文方法对图像进行去运动模糊。其中：图7(a)为原始清晰图像；图7(b)为模糊噪声图像；图7(c)为使用MLP方法去除运动模糊后的结果图，图7(d)为使用边缘检测方法去除运动模糊后的结果图，图7(e)为使用本文提出的算法去除运动模糊后的结果图。PSNR值如表1所示。由表1知，MLP方法与边缘检测方法去除运动模糊的PSNR值相差不大，但是MLP方法会放大噪声，边缘检测方法可能会给图像带来振铃效应。而本文方法的PSNR值在对比实验中值均明显高于其他两种方法，而且放大噪声与振铃效应均不明显，去运动模糊效果明显优于其他两种方法，这就表明本文算法能够有效地移除图像运动模糊。

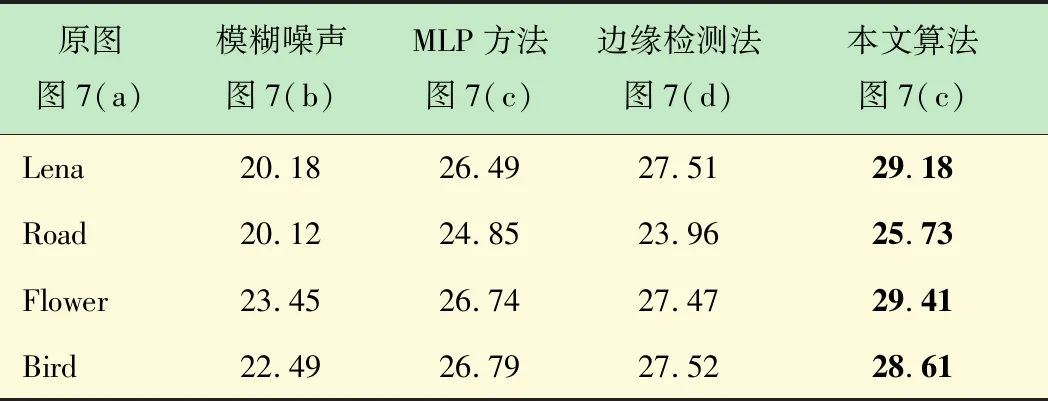
表1 不同方法的PSNR值 dB

4 结 语

本文提出一种基于梯度域和深度学习的图像运动模糊盲去除算法，将CNN可以学习图像自身特征的性能用于去模糊的问题中，设计了一个有效的CNN结构;将图像梯度域预处理与CNN网络相结合的方法，避免直接用CNN网络而忽略图像先验信息的缺点。实验表明，本文方法不仅能有效去除图像运动模糊，同时很好地保留了图像细节，放大噪声不明显，较好地抑制了振铃效应的产生。