顶管施工引起地表竖向变形分析

苏 越，张 敏，李更召，张成君，邢卫民

(天津市勘察院， 天津 300191)

城市市政基础建设中，由于路面交通繁忙，人员密集，地面建(构)筑物及地下管线复杂，敷设新的地下管道采用以往的开槽方案已经越来越困难，为了减少对正常活动的干扰以及房屋的拆迁，非开挖施工已经成为市政管道施工的最佳方案。顶管法是地下管道非开挖施工的一种，利用主顶油缸或管道间中继站的推力，把掘进机和管道从工作井内推入土层并一直顶推到接收井内，其优越性在修建穿越河流、道路和已有构筑物的地下通道、管道等地下工程得到体现，但顶管施工也不可避免地造成地面和地下土体的移动,即沉降和位移。

李庆臻[1]、肖雁征等[2]、曹明明[3]通过分析具体案例的地表变形情况，探索顶管施工对周围土体变形影响机理及影响范围。吴大国等[4]、高坤[5]、刘营[6]、张海生[7]、宋建学等[8]通过三维数值模拟，探索顶管引发周围土体变形的主要影响因素，并对实际项目变形提供预测分析。关永平[9]、夏永发[10]、何桥等[11]通过模拟计算，分析不同土体参数及环境参数对变形的影响，认为顶管与建筑物水平间距、建筑物基础埋深以及土体参数是控制变形量的主要参数。任毅[12]、刘航军等[13]通过实际工程案例，探索地表变形随时间发展情况，认为顶管引发地表变形分为机头到达前沉降、施工扰动沉降、管土间隙沉降及土体固结沉降四个阶段。董晓娟等[14]、韩国良[15]、潘建立[16]对前人工作经验进行总结，提出了刀盘附加推力、摩阻力、注浆压力和土体损失是造成土体变形的主要影响因子，并提供了若干计算方法。

本文对前人工作进行总结，假定土体不排水，利用弹性力学Mindlin解推导了正面附加推力、设备与周围土体的摩擦力对地表垂直变形的影响，结合土体损失引起的竖向变形，得到顶管施工引起的总的土体垂直变形计算方法，并通过天津某地区顶管施工实测数据进行了验证，监测数据与计算结果匹配度较高。

1 工程概况

天津某雨污水管道工程某标段，管线沿道路中心线穿越城区一交通要道，采用顶管施工，车辆照常通行。本场地地势总体较平坦，地基土分布较尚稳定，埋深20 m范围内主要土层如下：①2素填土层，厚度1.5 m，可塑状态，中压缩性土；④1粉质黏土层，厚度2.5 m，软塑—可塑状态，中压缩性土；⑥2淤泥质粉质黏土层，厚度8.5 m，软塑—流塑状态，高压缩性土；⑥4粉质黏土层，厚度7.5 m，中压缩性土；表层地下水属潜水类型，静止水位埋深1.0 m。

该标段顶管长度53 m，管顶覆盖土层厚度2.6 m，采用泥水平衡顶管方法进行施工，顶管外径2.4 m，管节厚180 mm，采用预制C40混凝土管节，每节长度为3 m，如图1所示。

图1顶管剖面示意图

2 顶管施工对地表竖向位移影响因素分析

顶管施工中引起土体变形的因素主要有：

(1) 地层损失造成沉降。顶管顶进时，掘进面土体应力较大，土体会向顶管内移动塌落，由于土体的松动范围超出工具管范围，会造成顶管周围的土层也被松动，因此地层有了损失。注浆填充可减缓土体损失但并不能完全消除此因素影响。

(2) 正面附加推力与土压力无法保持平衡。开挖临空面依靠附加推力与土压力的平衡保证稳定的出土，实际操作中，由于临空面土质条件复杂，会有附加推力与土压力偏差较大情况出现。若附加推力大于土体的被动土压力，会造成土体的挤压变形，若附加推力小于土体的主动土压力，则会造成土体的坍塌。

(3) 顶管与土体摩擦力带动周围土体移动。顶进过程中掘进机以及后续管节均会对周围土体产生摩擦力，一般情况掘进机与土体的接触面积更大从而产生更大的摩擦力，后续管节通过注浆等工序可以降低摩擦力。

3 顶管施工引发土体变形计算

3.1 基本假定

(1) 本文仅考虑施工期间的变形，土体为不排水固结变形。

(2) 为简化计算，对顶管上方土体参数取加权平均值，简化为均质线弹性半无限体黏性土。

(3) 顶管推进面附加推力为圆形均布荷载。

(4) 顶管与周围土体的摩擦力均匀分布。

3.2 地层损失造成沉降计算

Peck提出地面沉降槽呈正态分布，假定土体体积不可压缩，则土体损失量即为沉降槽体积，地面沉降计算公式为：

(1)

(2)

式中：x为计算点沿顶管方向坐标，m；xi为隧道开挖面起始点，m；xf为当前隧道开挖面位置，m；Ф为由标准正态分布函数查表获得；S(x)为沿顶管方向计算点竖向沉降量，m；Smax为顶管轴线正上方最大竖向沉降量，m；i为地面沉降槽宽度系数，m，取值如下：

i=R(h/2R)n

(3)

R为掘进机外半径，m；h为顶管轴线至地面距离，m；软黏土中，n=1。

Vloss为隧道单位长度土体损失量，根据经验方法[5]选择合适的挖掘面百分率来估算土体损失：

Vloss=πR2η

(4)

黏土中，η取值为0.5%～2.5%，结合本地区施工及监测经验，本次计算η取值为1.5%。

3.3 正面附加推力造成土体垂直变形计算

图2为正面附加推力造成土体垂直变形计算模型，采用弹性力学明德林解计算圆形均布荷载作用下，土体中任一点(x,y,z)在z方向产生的位移计算如下：

图2力学模型简图

(5)

式中，

式中：P为掘进正面附加推力，kPa；D为掘进机外圈直径，m；h为管道中轴线至地面距离，m；G为土的剪切模量，MPa。

(6)

式中：Es为土体压缩模量，MPa；K0为静止土压力系数；μ为土体泊松比。

3.4 摩擦力造成土体垂直变形计算

由模型图2可以看出，顶管对周围土体的摩擦力，分为掘进机和后续管道两部分，因两者均是圆柱体，取表面微分面积Rdrdθ，利用明德林解积分土体中任意一点(x，y，z)沿z方向的位移为：

(7)

式中，

式中：p为圆柱体与周围土体之间单位面积摩擦力，kPa，等于法向应力乘以摩擦系数，法向应力近似取最大埋深处的垂直土压力，摩擦系数根据桩土界面系数取值。

3.5 土体总的垂直变形计算

去除注浆、纠偏等施工过程中不可控因素，地表竖向变形主要由以上三部分即地层损失、正面附加推力、摩擦力造成，总的地表竖向变形为：

w=Sloss+w1+w2

(8)

4 计算结果分析

本项目参数取值：h=3.8 m，R1=1.2 m，D=2.42 m，L=3 m，L1=50 m，P=20 kPa，p掘进机=20 kPa，p后续管道=4 kPa，Es=2.5 MPa，μ=0.35，K0=0.51，G=0.6 MPa，η=1.5%，i=1.9 m，xi=-53.0 m，xf=0 m。

计算y=0时土体损失、正面附加推力、掘进机及后续管道摩擦力单独作用以及共同作用下引起的地面纵向垂直变形，计算结果如图3所示。

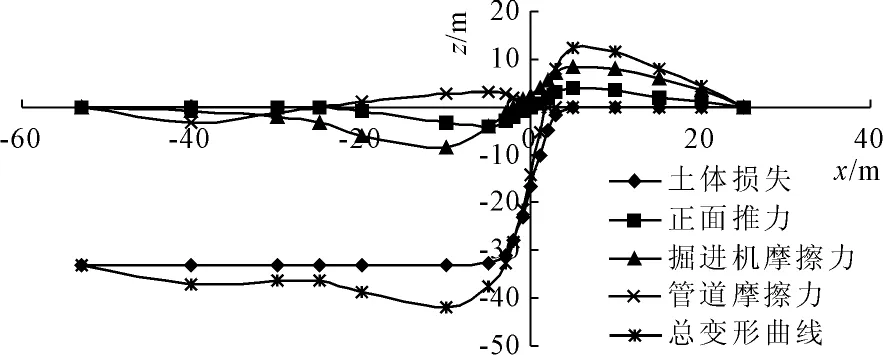
图3各因素引发地表纵向变形曲线

图中计算结果显示如下规律：

(1) 地面沉降主要由土体损失造成，当x>3D时，地表变形受土体损失影响较小接近于0，当x≤3D，沿x轴反方向沉降逐渐增大，开挖面位置沉降量为最大沉降量的50%，至x=-3D沉降达到最大值并趋于稳定。

(2) 正面推力造成地表竖直变形表现为前方隆起，后方沉降，并以开挖面为轴线反对称分布。

(3) 摩擦力造成地表竖直变形同样表现为前方隆起，后方沉降，但是对称轴线分别为掘进机中线位置和后续管道中线位置。

(4) 受综合因素影响，地表纵向变形曲线可分为：隆起区—急速沉降区—沉降稳定区—沉降回弹区，最大隆起位置在开挖面前方2.5D位置处，最大沉降值出现在距离开挖面1.3h后方。

计算不同纵断面处地表沿横断面变形曲线，选取y=-5 m、0 m、+5 m，分别对应纵向沉降极值位置、开挖面位置、纵向隆起极值位置，计算结果如图4所示。

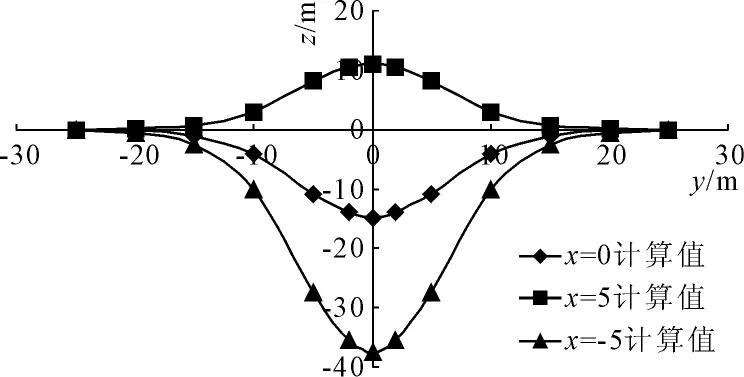
图4不同纵断面处地表沿横断面变形曲线

由图4计算结果显示如下规律：

(1) 无论是隆起或是沉降，顶管正上方位置变形最大，向两侧方向逐渐消散。

(2) 在横断面5h范围之外，地面变形接近于无，可认为5倍顶管深度范围外变形不受顶管影响。

5 实际监测结果对比

为对比试验结果，顶管施工期间在地表布设竖向位移监测点测量地面变形，监测点位布设如图5所示。

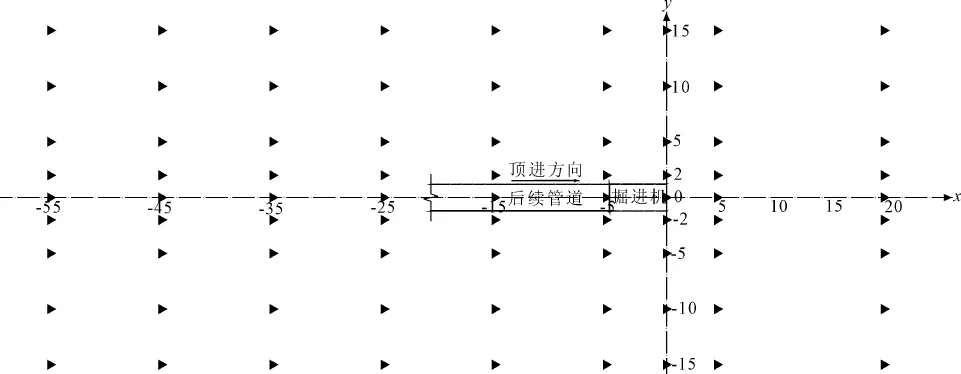
图5监测布点图

监测点以顶管轴线对称布置，各测点距离中轴线分别为2 m、5 m、10 m、15 m。共布设5个断面，分别位于顶进面正上方、正前方5 m、20 m、正后方5 m、15 m、25 m、35 m、45 m、55 m。测量此施工节点各测点变形稳定值，并与计算结果对比，对比结果如图6、图7所示。

图6地表横断面变形实测值与计算值对比图

图7地表纵断面变形实测值与计算值对比图

由以上结果可以看出，各断面最大变形实测值略小于计算值，是因顶管推进过程中桩土界面摩擦系数减小导致，曲线形状基本吻合，说明本文计算方法正确，理论值偏于保守。

6 结 论

本文假定土体为均质线弹性半无限体，变形形式为不排水固结，并假定顶管与土体之间作用力均匀分布，引入Peck公式计算土体损失引起的变形，并采用明德林解积分正面推力以及摩擦力造成的土体变形，此三者共同作用，使得顶管上方地表呈现规律性的垂直位移，并把计算结果与实测值进行对比，验证了本计算方法的正确性。

此次研究仅针对某一特殊节点地表的变形分布规律，关于顶管施工期间地表变形随时间的推进而呈现的变化规律未作研究，另外，因现场条件限制，未能对比地表下土体的变形规律，可作为今后研究方向。