全填塘换填路基抗浮数值分析研究
2019-07-02刘振华修占国
刘振华,王 帅,陈 泽,修占国
(1.中建五局华东建设有限公司, 浙江 平湖 312400;2. 东北大学 资源与土木工程学院, 辽宁 沈阳 110819)
在地下水位较高的地区,尤其是闽江浙地区,修建公路不可避免地会遇到一项重大的技术问题——浮力。如何避免浮力过大危及公路安全成为现在公路发展的焦点问题。而对于一些软弱地下土层,水浮力过大问题将更加凸显。对于这一问题,可采取的措施有以下几种:(1) 路基下排水[1-2]:将路基下的水全部排出,降低路基下地下水位,但此方法只适用于地下水位较低的地区,江浙等东南沿海地下水位较高地区,想要使水位降低,需要花费的代价过大;(2) 路基压实[3-6]:填好路基后,用机械将路基压实,再填筑再压实,如此循环以达到抗浮目的;(3) 换填路基[7-8]:挖出路面以下的软弱土层,用换填材料来进行填筑,以提高路基的黏聚力、防水性以及耐久性。
鉴于此,本文以全填塘这种软弱地基为例,来对路基换填的抗浮效果进行数值模拟分析。本文以全填塘换填路基为模型,不断变换路基换填材料,以此来改变换填部分的弹性模量、重度、黏聚力和内摩擦角,通过比较分析找出影响全填塘换填路基抗浮效果的主要因素以及得到最理想的换填材料。
1 工程概况
平湖市位于其辖区内的嘉兴市,南邻杭州湾,水系复杂,水位较高。本项目为平湖乍浦至上海兴塔的混凝土公路(01省道至平兴公路段)K8+110.000—K16+780.185路段,依据原交通部颁布的《公路工程技术标准》[9](JTG B01—2003)一级公路的标准,又考虑到城市道路部分功能,所以除局部受限的路段(K2+850—K3+600杭浦跨线桥处)设计速度是60 km/h外,余下路段的设计速度都取80 km/h。由于距该路段5 m处存在一个小型水塘,故该路段路面以下2 m处存在大量淤泥,且路面以下地下水位较高,严重影响了路基的承载能力,故根据工程需要,对该路段公路进行路基换填设计。具体的横断面布置情况如图1所示。
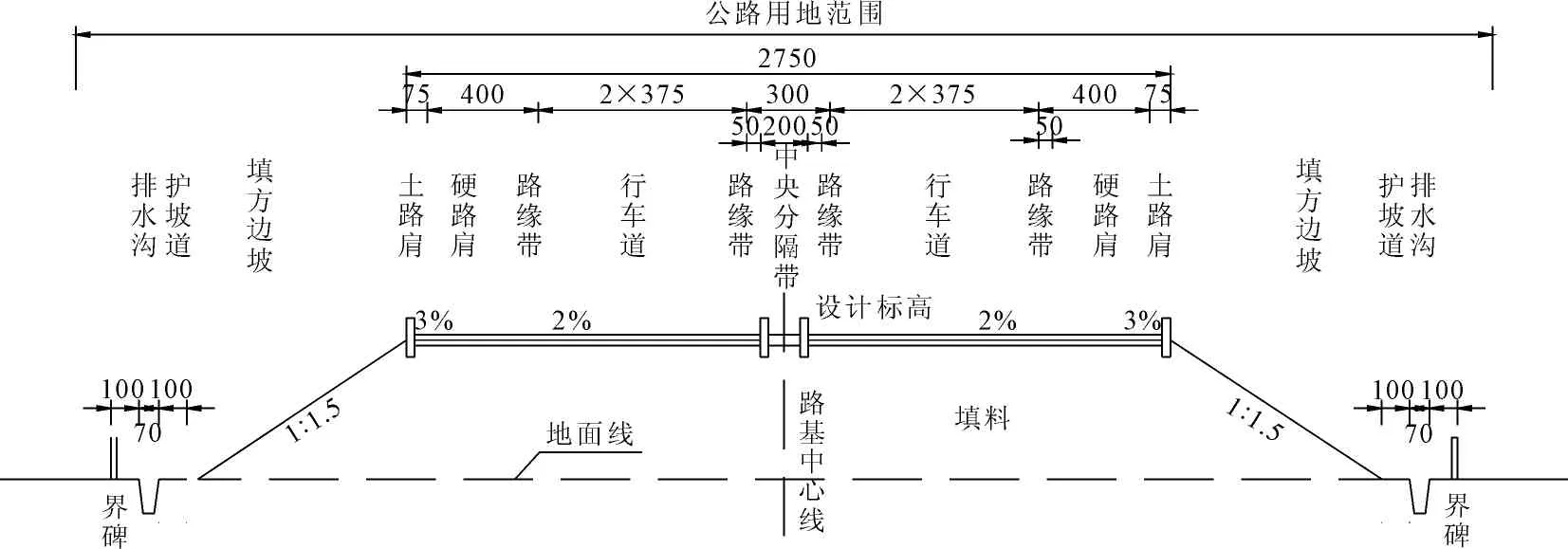
图1K8+110.000—K16+780.185标准横断面(单位:cm)
K8+110.000—K16+780.185段路基宽度27.5 m,路幅布置如下:0.75 m土路肩+4.00 m硬路肩(含0.50 m路缘带)+2×3.75 m行车通道+2×3.75 m行车通道+4.00 m硬路肩(含0.50 m路缘带)+0.50 m路缘带+0.75 m土路肩+2 m中央分隔带。
根据图1路基标准横断面图,可以得出路基的各部分尺寸及参数,进而可以建立如图2所示的路基换填模型图。
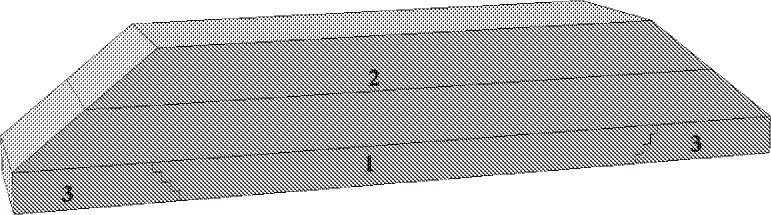
图2换填路基模型
2 全填塘换填路基设计
2.1 路基抗浮稳定性计算
对于该项目地下水位较高地区,路基抗浮的验算与地下结构抗浮的验算相似。路基的浮起开裂不仅是地下水的浮力作用,而且在基坑回填土未夯实的情况下或路基周边为富含水的深厚杂填土等透水土层及在雨水等地面水的长期作用下,路基路面都会发生浮起、结构损坏的现象,因此路基路面设计时也应进行抗浮验算[10-13]。
抗浮验算包括整体抗浮稳定验算和局部抗浮稳定验算以及路基内结构构件的强度、刚度验算。这里主要对整体抗浮稳定验算和局部抗浮稳定验算做简要概括。
2.1.1 整体抗浮验算
对于常年地下水位较高地区(如广东、上海等),按照广东省规范[14]进行整体抗浮验算:

(1)
式中:W为换填宕渣重量与宕渣上其余活荷载重量之和;F为地下水的浮力;Kw为抗浮稳定安全系数,一般取1.05。
在本论文中,可以取2 m长路基进行验算,经现场测量,换填前路基总重量W为2 437 kN,而地下水浮力可以通过下面公式进行计算:
F=ρgh×S=2 695 kN

对于路基总重量大于水浮力的路段,应注意施工期间的降排水措施,主体结构施工期坑槽尚未回填,一旦停止降水,地下水位将很快回升。而且规范中要求,如果单纯考虑施工期间的水浮力,需要以一个水文年的最高水位来预测抗浮设防的水位[15]。
2.1.2 局部抗浮验算
局部上浮是指路基总重量大于水浮力,但某一段路基直接承受水浮力且其压力小于浮力,整段路基不同部位抗浮承载力不均衡,出现局部位移。这时路面往往会发生局部浮起,因此应特别注意局部稳定性的验算,在路基整体稳定性得到保证的前提下,对路基表面进行强度和抗裂验算[16]。
2.2 填料
2.2.1 填料材料
路基直接填筑填料的液限应小于等于50,塑性指数小于等于26。有些材料不能直接填筑路基,如:泥潭、淤泥、土中有机土的含量超过允许值的土等。
(1) 粉质黏土。当本项目K8+100.000—K16+780.185路段采用粉质黏土填筑时,粉质黏土要求黏粒含量在30%~40%之间,且砂粒组的含量小于粉粒组的含量,塑性指数介于12~15之间。
(2) 砂土。当本项目K8+100.000—K16+780.185路段采用砂土填筑时,砂土最大粒径要求不大于35 mm,不小于15 mm,颗粒级配良好。
(3) 宕渣。当本项目K8+100.000—K16+780.185路段采用宕渣填筑时,宕渣要求粒径不大于150 mm,含泥量小于等于10%,粒径大于40 mm石块的含量不小于30%。
2.2.2 地基表层处理
(1) 路基填土前应考虑先清理草皮、树根及腐殖土等,一般填方路段清表应按20 cm考虑。清表后,在其下20 cm土层中加5%石灰进行翻拌整平。然后再进行碾压至密实,碾压下沉应按10 cm考虑,基底压实度(重型)不应小于90%。
(2) 在原始地面上直接填筑路堤要求地面横向的坡度小于1:5.0,而当地面横坡坡度较小时,如1:5.0~1:2.5时,需要在原地面铺设台阶,台阶挖成向内侧倾斜的样式,且其坡度为4%,且台阶的宽度应大于2 m。
(3) 清除的表土需要结合附近的地形进行集中堆放,以方便绿化防护(边坡、中央分隔带等部位),禁止用于路基填筑。
3 全填塘换填路基模型建立及数值分析
路堤经过的水塘路段,需先开始围堰、排水及清淤处理,清淤换填及河塘用砂土、粉质黏土或宕渣来进行填筑。然后分别对这三种材料填筑后的路基建立模型,进行数值模拟分析,比较三种情况下路基所受压应力及其位移大小,从而找出抗浮的最优填筑材料。
3.1 模型建立
运用ABAQUS软件,对路基建立1∶1比例的模型。填塘路基的路基宽度B为27.50 m,塘基平均处理宽度L1为28.4 m,塘深h为1.8 m。假定地下水位与地表齐平,且路基是一个均匀、连续、完全弹性的整体,其弹性在所有各个方向都相同,且其位移和变形是微小的。此外,由于路基面积较大,重度较高,故路基上表面和侧面位移和转角相对较小,所以假定路基上表面和侧面的位移和转角均为0。
依据上述假定,建立如图2所示的路基模型。
然后将模型分为三部分:1部分为换填部分;2部分为地表以上路基部分;3部分为地表下路基换填部分两侧路基。模型中三部分土体的本构关系均采用摩尔-库仑模型,具体参数见表1。
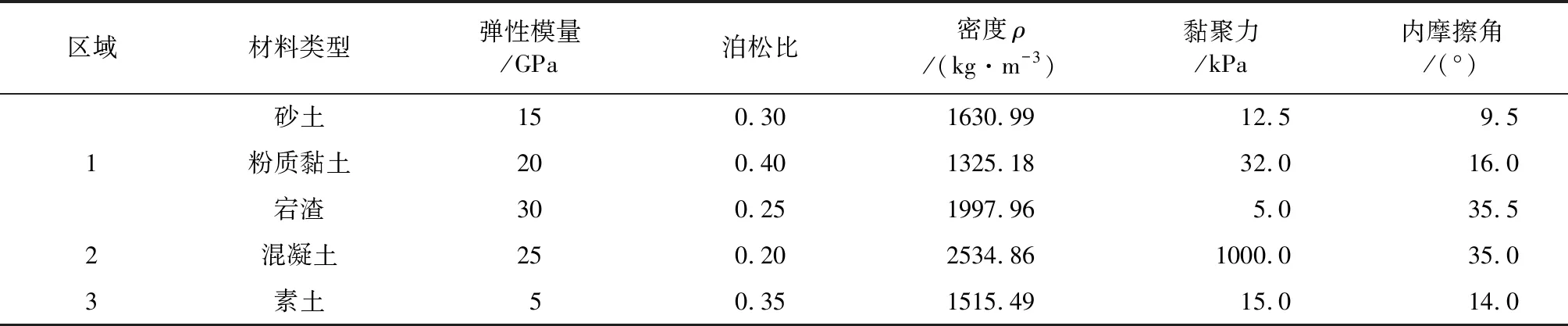
表1 模型各部分参数
3.2 加载及网格划分
由于地下水的渗透,全填塘换填路基所受水浮力为路基1、3部分整体受到的水浮力。下面给出水的重度γ:
γ=ρg=9.81 N/m3
由于路基面积较大,重度较高,故道路上表面和侧面位移相对较小,可忽略不计,故在道路上表面和侧面加上约束三个方向位移均为0的边界条件。
网格划分采用C3D6(六节点三棱柱)楔形单元,扫掠划分网格,共划分1 374个单元。模型网格划分见图3。
3.3 数值模拟分析
分别对用粉质黏土、砂土和宕渣填筑的路基模型进行数值模拟分析。
(1) 以粉质黏土为路基填筑材料得到模拟结果如图4所示。


图3 模型网格划分图
图4以粉质黏土为材料模拟位移图
由图4可知:路基换填部分产生的位移稍小于未换填部分产生的位移,相差6 mm左右。由此可以看出:用粉质黏土换填路基虽然可以增大换填部分的弹性模量与重度、减小换填路基的变形,但对变形的减小并不明显。
此外,换填部分中心区域出现变形较大的情况,说明换填的粉质黏土强度不足,对路基抗浮提高不大。
(2) 以砂土为路基填筑材料,得到图5所示路基模型位移云图。

图5以砂土为材料模拟位移图
由图5可以发现:以砂土为路基填筑材料,填筑部分位移虽然也是稍小于两侧未填筑部分位移,但是换填中心区域位移为8 mm左右,未出现较大变形,可见换填砂土后的路基强度强度明显高于用粉质黏土换填后的路基强度。
(3) 以宕渣为材料来填筑路基,经过ABAQUS模拟计算得到图6所示位移云图。

图6以宕渣为材料模拟位移图
由图6可知:采用宕渣换填路基后,换填部分位移相比于未换填部分位移有明显降低的趋势,减小20 mm左右。说明宕渣是路基换填抗浮的可靠材料。
而从路基上表面及路基两侧面位移几乎为零可以看出是约束条件起了作用。路基底面两端出现位移急剧下降的现象则是由于路基两侧面均采用铰接的方式固定边界。
由以上三种换填材料对比分析后,可得出宕渣作为路基换填材料较为合理。
至于1部分与3部分的交界处,则是换填路基的最薄弱处。从图中也可看出其位移较大,在后续研究中可以考虑采用锚杆或桩基横向固定交界处的措施。
4 结 语
本文主要研究换填材料对路基抗浮效果的影响情况,借助ABAQUS软件对分别用粉质黏土、砂土、宕渣等材料进行换填后的路基模型进行模拟后,可以得出结论:换填的粉质黏土强度不足,对路基抗浮提高不大;换填砂土后的路基强度明显高于用粉质黏土换填后的路基强度;而换填砂土后的路基强度又高于用其余两种材料换填后的路基强度。进而可以得出:在换填的粉质黏土、砂土、宕渣等材料中,宕渣的抗浮效果最好。
