供应商产出随机与供应中断下的双源采购决策

2019-07-02陈崇萍陈志祥

中国管理科学 2019年6期

陈崇萍，陈志祥

(1.华南师范大学公共管理学院，广东广州 510006;2.中山大学管理学院,广东广州 510275)

1 引言

制造商在进行物资(原材料或零部件)采购时,常常面临供应商的两类不确定风险——产出随机风险和供应中断风险。这两种供应风险都对制造商的正常生产活动产生严重的影响。因此研究采购决策中供应商随机产出和中断风险对制造商的影响，对指导制造商更好做出科学的采购决策有重要意义。

供应商产出随机是很常见的，主要是因为生产受到自身条件的限制，如机器故障、工序复杂等，造成供应商有效产量低于计划产量。这种情况在一些电子元器件与芯片的生产中特别常见。因为这些元器件生产过程相当精密，生产的产品通常在出厂验货时才发现大量的产品不合格，导致有效产量极低，如液晶显示器的平均有效产量通常小于50%[1]。同时，供应中断的情况也不少见，且一次意外供应中断就有可能给制造商带来难以弥补的损失。如2011年3月11日，日本地震导致丰田公司400多种零部件短缺，生产量减少了相当于日常6个多月的产量,损失惨重[2]。再如2004年，生产流感疫苗的生产商凯隆(Chiron)由于其唯一的供应商遭受细菌污染而生产暂停，导致美国产生了严重的流感疫苗短缺事件，美国政府不得不控制疫苗的配给，同时很多州疫苗价格暴涨[3]。

为了减轻由于供应产出随机和供应中断带来的损失，同时也为了提高制造商与供应商洽谈采购交易合同中的价格谈判能力，降低采购成本，大部分的制造商都双源采购[4]。双源采购成为制造商应对供应中断的主要风险管理策略。因为面对概率低的非常规突发事件，双源采购是最优的[5]。

双源采购因能有效降低采购风险而被全球的公司广泛的采用[6]。如世界上最大的工程机械与矿山设备生产商美国卡特彼勒公司就双源采购，他们向一个低成本公司采购日常需求稳定的材料，同时向另一个快速生产但价格贵的生产商采购紧急需要的材料[7]。研究发现，双源采购的另外一个优势是采用两个供应商能形成竞争，从而为装配企业获得更好的采购价格与质量[8]。

本选题基于多年来我们对我国汽车行业调研发现的现实问题。在调研中我们了解到，中国多数汽车企业，如长春一汽，柳州五铃，武汉神龙、重庆长安、广汽本田和丰田等，在采购中经常遇到供应商产出随机和供货中断的情况。由于这些大型的汽车装配商的场地有限，准备的安全库存也非常有限，遇到供应中断的情况，只能暂停生产。从制造商处我们了解到，汽车制造商的生产线每停止一分钟的生产，损失都非常大。同时，遇到这种情况，最快解决也需要一天左右的时间，汽车制造商因此损失惨重。所以汽车制造商不得不采用双源甚至多源的采购模式，以降低生产被中断的可能性。同时这些企业的供应商也都经常存在有效产量很不确定的情况，这种情况影响给制造商的有效供货量从而影响制造商的生产。面对供应商的产出随机和供应中断，如何合理确定最优的双源采购订货量，对这些汽车企业有重要意义。

国内外对双源采购问题进行了不少研究，与本研究有关的主要是产出随机下的双源采购和供应中断下的双源采购研究。目前国内外研究供应商产出随机下的双源采购文献很多，主要有Tomlin和Wang[9]采用报童模型研究了供应产出不确定情况下最优的双源采购策略。Zhu[10]研究了两个供应商具有不同的产出不确定性、生产成本和提前期时最优的双源采购动态库存策略。Ju等[11]研究了供应商的产出满足伯努利分布时最优的双源采购策略。Jaksic和Fransoo[12]根据提前期长的生产商生产成本提高的新情况，研究了就近生产企业生产能力存在限制情况下的双源采购问题。Wan和Chen[13]采用期权和现货市场两种方式研究了多周期双源采购供货问题，研究发现有期权策略比没有期权时的采购策略要好。

与此同时，对供应中断风险下的双源采购问题的相关研究在近几年也有增加，如Iakovou等[14]研究了两个供应商都存在供应中断风险时，制造商双源采购最优的订货策略，但没有考虑供应商的产出随机。Sawik[15]研究了在供应中断的情况下，同时考虑供应商选择和消费者订单排序问题时比较了双源采购和单源采购的优劣。Lücker和Seifert[16]采用库存、双源采购和柔性生产能力三种策略保证医药供应链的可持续性，研究发现当没有双源采购策略时，库存策略和柔性生产能力之间可以替代，但有双源采购时，双源采购与柔性生产能力之间就可以替代。Lena和Stefan[17]在供应中断的情况下，研究了供应商存在学习效应时最优的双源采购策略。汪传旭和许长延[18]也考虑了供应中断情况下，两个零售商相互转运的最优策略。在供应中断和生产成本不确定的情况下，黄河等[19]研究了买方与卖方均可努力改善产出随机又可降低生产成本的情况下，供应链的最优决策。陈崇萍等[20]研究了双源采购如何质量统一的问题。

现有研究有的将供应中断和产出随机简略的作为同一种风险考虑，有的仅考虑产出随机或供应中断。但是，现实中产出随机和供应中断风险表现形式和严重程度是不同的，刻画两类风险的方法和管理策略也不同。产出随机是一种连续风险，而供应中断是一种随机性的风险。因此区别两类风险在采购决策中的表现，可以更好的分析与应对这两种风险。本文的贡献在于，将现实中存在的产出随机风险和供应中断风险在双源采购模型中同时且分开表现，充分考虑到两种风险的不同表现形式，分析研究了此时双源采购的最优决策问题，为企业更好的应对这两种风险提供更好的指导。

2 问题描述、符号说明与基本假设

本文研究的概念模型如图1所示：假设一个制造商同时向供应商1和供应商2采购同一种零部件。供应商i(i=1,2)没有出现中断风险的概率为θi，则出现中断风险的概率为(1-θi)。供应商1中断风险可能性低价格高，供应商2中断风险可能性高价格低，即ω1>ω2，(1-θ1)<(1-θ2)。且每个供应商的产出具有随机性，即计划生产量为xi(i=1,2)时，有效产量仅为αixi，其中αi表示产出随机因子，影响产出随机因子的主要是供应商的生产条件、技术水平等，αi∈[mi,1]的均匀分布，其概率密度函数与分布函数分别为fαi(αi),Fαi(αi)。

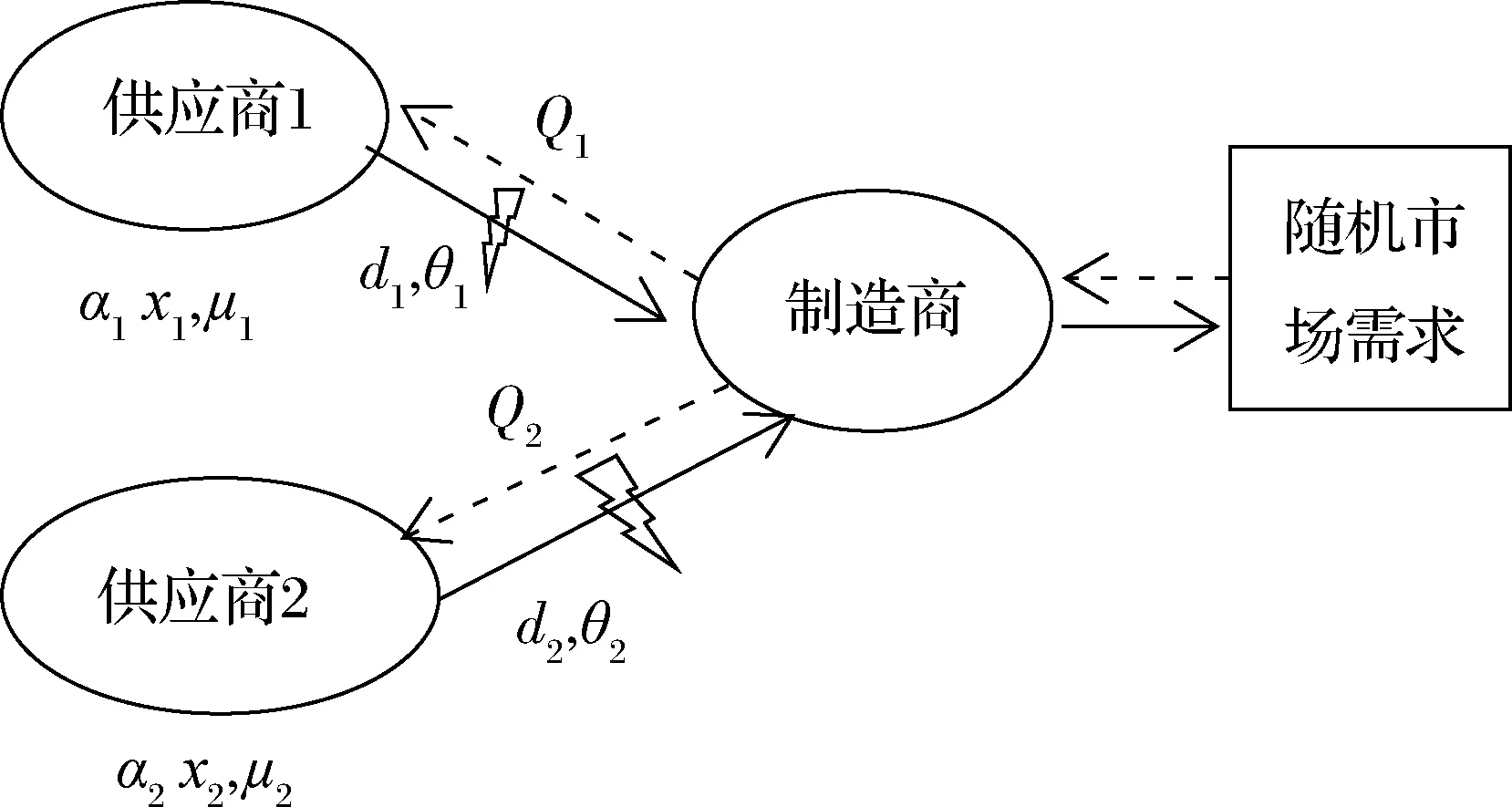
图1 供应商产出随机与供应中断时的双源采购概念模型

假设最终产品的随机市场需求用y表示，其概率密度与分布函数分别为fy(y),Fy(y)。最终产品的市场售价为p，未销售的产品单位残值为s，单位缺货损失为ν。且在本文中出现的任何变量，均有n+=max(0,n)。

在下面所有的符号中，我们用下标a表示只考虑供应商产出随机时的各变量，用下标b表示同时考虑供应商产出随机与供应中断时的各变量。

研究中假设制造商与2个供应商均为风险中性的，且信息对称，决策者完全理性。

3 模型构建

本文分别针对两种情况建立博弈模型：(1)只考虑供应商产出随机，(2)同时考虑供应商产出随机和供应中断。

3.1 只考虑产出随机时最优决策

本研究中，制造商是斯坦伯格博弈的领导者，首先决定向两个供应商的订货量，然后两个供应商再根据制造商的订货量决定自身的生产量。这种假设确实与现实情况相符，如很多大型汽车装配企业，拥有强大的资金与技术实力，零部件供应商跟随装配企业的决策而决策。根据决策的先后顺序，我们采用反向求解的方法，即首先求解供应商的最优生产量，然后求解制造商的最优订货量。

3.1.1 供应商最优生产量

在制造商给定的价格ωi下，供应商的计划产量为xia(i=1,2)时，供应商i(i=1,2)给制造商的供货量为dia(dia=min(Qia,αixia)，此时供应商i的利润函数为：πia=ωidia-cixia

因此供应商的期望利润为：

Πia=ωiE(dia)-cixia

(1)

可知供应商最优的生产量满足如下条件(证明详见附录I)：

(2)

3.1.2 制造商最优的订货量

假设此时制造商向供应商i的订货量为Qia，有dia(dia=min(Qia,αixia)。以下都有：当i=1时j=2;当j=1时，i=2。制造商利润函数用πa表示为：

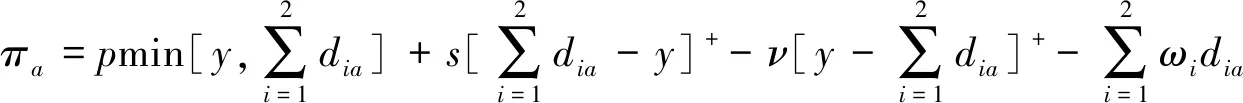
(3)

制造商此时的期望利润用Πa表示为：

其中的Aa,Ba,Ca详见附录II。

定理1只考虑供应商产出随机时，存在唯一向两个供应商的最优订货量使得装配企业利润最优。

证明:对制造商期望利润函数(3)式求向供应商i的订货量Qia的一阶导数为：

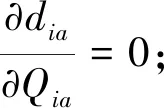
(5)

对(5)式求订货量Qia的二阶导数得：

+min(Qja,αjxja)]+(p+ν)-ωi]

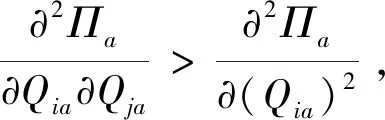
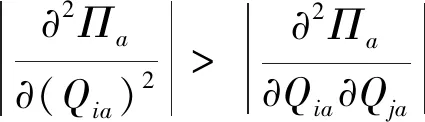
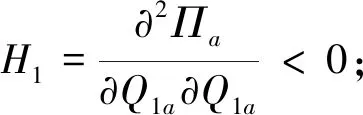
由以上证明可知，海塞矩阵是负定的，也就是以上函数存在唯一最大值，证毕。

-(p-s+ν)E[Fy(Qia+dja)]+(p+ν)-ωi=0

(6)

因为每个供应商的生产量是根据制造商的订货量而决策的量，且因为存在生产扰动性，使得供应商的生产量不可能一直等于订货量，所以：

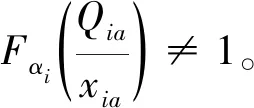
(7)

在以上的等式中，左边的销售价格p，单位缺货损失ν，单位残值s和采购价格ωi均是常数。

3.2 供应商产出随机和供应中断时最优决策

3.2.1 供应商最优生产量

类似3.1节的求解过程，我们首先求解供应商存在产出随机与供应中断可能性时最优的生产量。

在制造商给定的价格ωi下，供应商i(i=1,2)的计划产量为xib(i=1,2)时，供应商i给制造商的供货数量为dib(dib=θimin(Qib,αixib)，此时供应商i的利润函数用πib表示为：

πib=ωidib-cixib

此时供应商的期望利润用Πib表示为：

Πib=ωiE(dib)-cixib

(8)

可知供应商最优的生产量满足如下条件(证明与附录I类似，此处省略)。

(9)

3.2.2 制造商最优订货量

此时制造商每次可接收到供应商的供货量为：

制造商此时的利润函数用πb表示为:

因为：

-[y-db]+=-max[y-db,0]=(db-y)-(db-y)+

所以有：

min[y,db]=-max(-y,-db)]=db-max(db-y,0)=db-(v-y)+

以上利润函数可化简为：

(10)

制造商的期望利润函数用Πb表示为：

制造商此时的期望利润函数Πb也可表示为：

Πb=-(p-s+ν)Ab+(p+ν)Bb-νE(y)-Cb

(11)

其中的Ab,Bb,Cb详见附录Ⅲ。

定理2考虑供应商产出随机和供应中断时，存在唯一向两个供应商的订货量，使得制造商的利润最优。

证明:对制造商利润函数求向供应商i订货量Qib的一阶导数为：

类似3.1.2节有：

+ν)E[Fy(θiQib+djb)]+(p+ν)-ωi]

(12)

+ν)E[Fy(θiQib+djb)]+(p+ν)-ωi]

因:

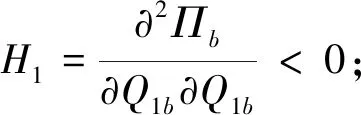
由以上证明可知，海塞矩阵负定，以上函数存在唯一最优解，也就是制造商存在唯一最优的向两个供应商的订货量使得自身利润最大，证毕。

最优的条件为：

(13)

4 算例与管理启示

4.1 最优决策与最优利润

假设一个制造商同时向两个供应商采购相同的关键零部件，制造商向两个供应商的采购价格分别为ω1=53,ω2=50，两个供应商的生产成本分别为c1=23,c2=20；两个供应商没有发生供应中断的概率为θ1=0.95，θ2=0.90;两个供应商均存在一定的生产不确定性，供应商i(i=1,2)的产出随机性因子αi满足[mi,1]上的均匀分布，则概率密度函数为fαi(αi)=1/(1-mi)。随机市场需求y∈[200,300]上的均匀分布，最终产品的市场销售价格p=150，未销售的产品单位价格s=70，每单位缺货损失ν=50。

由图2可知，制造商的利润关于两个供应商的订货量的图像有一个上凸的趋势，说明存在最优值，最优值在图像的最顶点处。

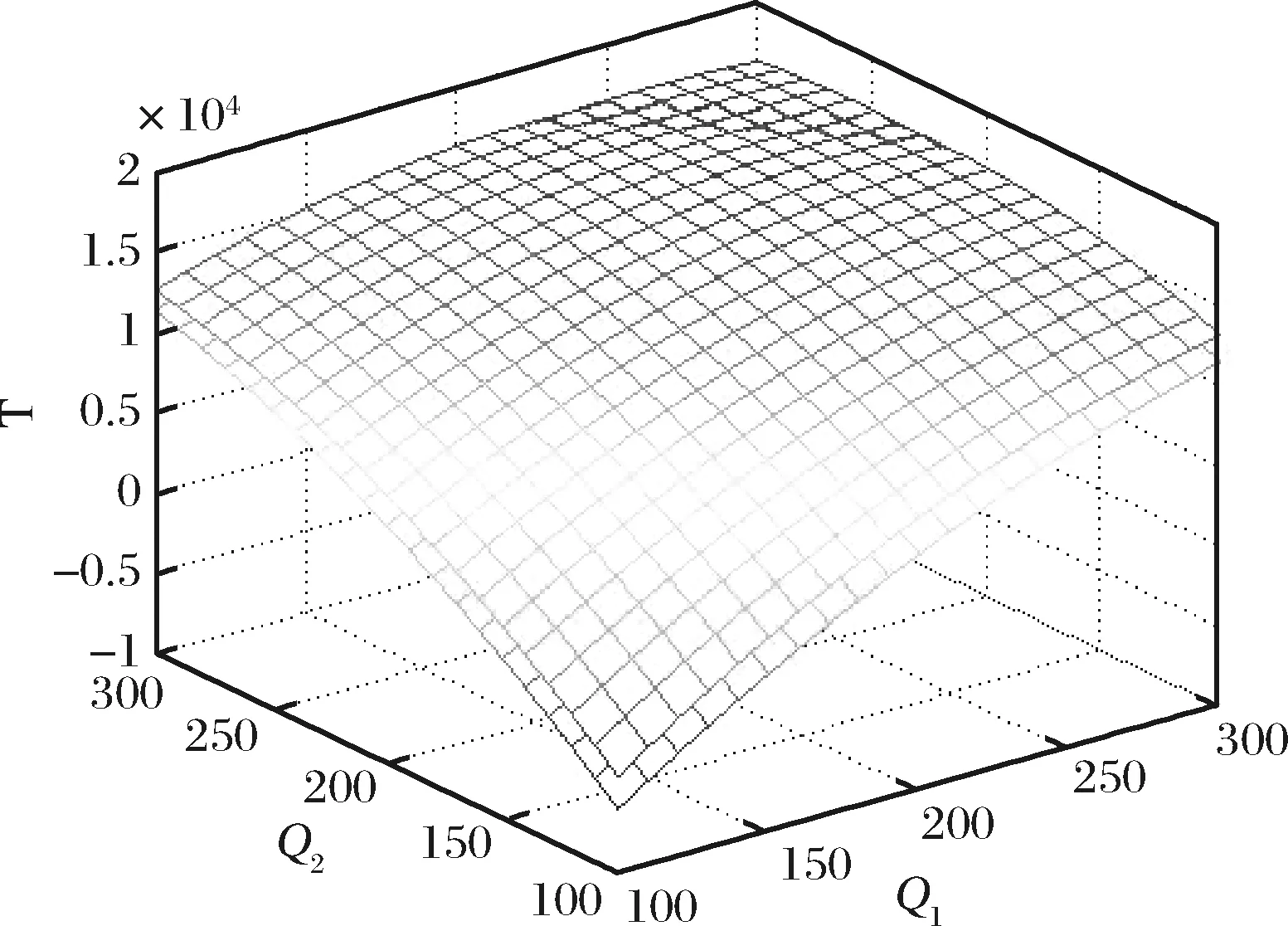
图2 两个订货量对造商利润的影响

以下我们分别求解两种情况下供应商最优的生产量，制造商最优的订货量。求解过程是：将以上基本参数代入各式，联立(2)与(7)式可解得:只考虑供应商产出随机时供应商最优的生产量(x1a,x2a)，制造商最优的订货量(Q1a,Q2a)，再将最优订货量和最优生产量代入(4)式和(11)式中可解得：制造商此时最优的期望利润(Πa)和两供应商最优的期望利润(Πia)；联立(9)与(13)式可解得:在同时考虑供应商产出随机和供应中断时供应商最优的生产量(x1a,x2a)，制造商最优的订货量(Q1b,Q2b)，然后将它们代入(11)和(8)式中可解得:制造商此时最优的期望利润(Πb)和供应商最优的期望利润(Πib)。且我们在求解中发现，确实只有一组非零解，与定理1和2的证明一致。

只考虑供应商产出随机与同时考虑供应商产出随机与供应中断时，供应商最优生产量与制造商最优订货量和最优利润，如表1所示。

表1 两种情况下的最优解

从表1中我们可以看出：考虑供应中断的情况下，制造商最优的订货量与供应商最优的生产量均比没有考虑供应中断时大，即x1aΠb。以上分析显示，考虑供应中断时，制造商应该多订货;同时供应商也应该多生产。

4.2 灵敏度分析

以下分析供应商产出随机性与供应中断可能性对最优决策的影响。

4.2.1 产出随机对最优值的影响

供应商的产出随机性不仅会对自身的决策造成影响，还会对制造商的决策与利润造成影响。以下将分析供应商产出随机变化对最优决策与最优利润的影响。由以上的分析可知，随着mi的增大，供应商i产出更稳定，有效产出更高。

按4.1节的计算过程，在只考虑供应商产出随机时，我们先增大m1的值，也就是让供应商1的产出更稳定，有效产量更高;然后增大m2的值，也就是让供应商2的产量更稳定，有效产出更高。可得各最优值如表2所示。从表2中可以看出：

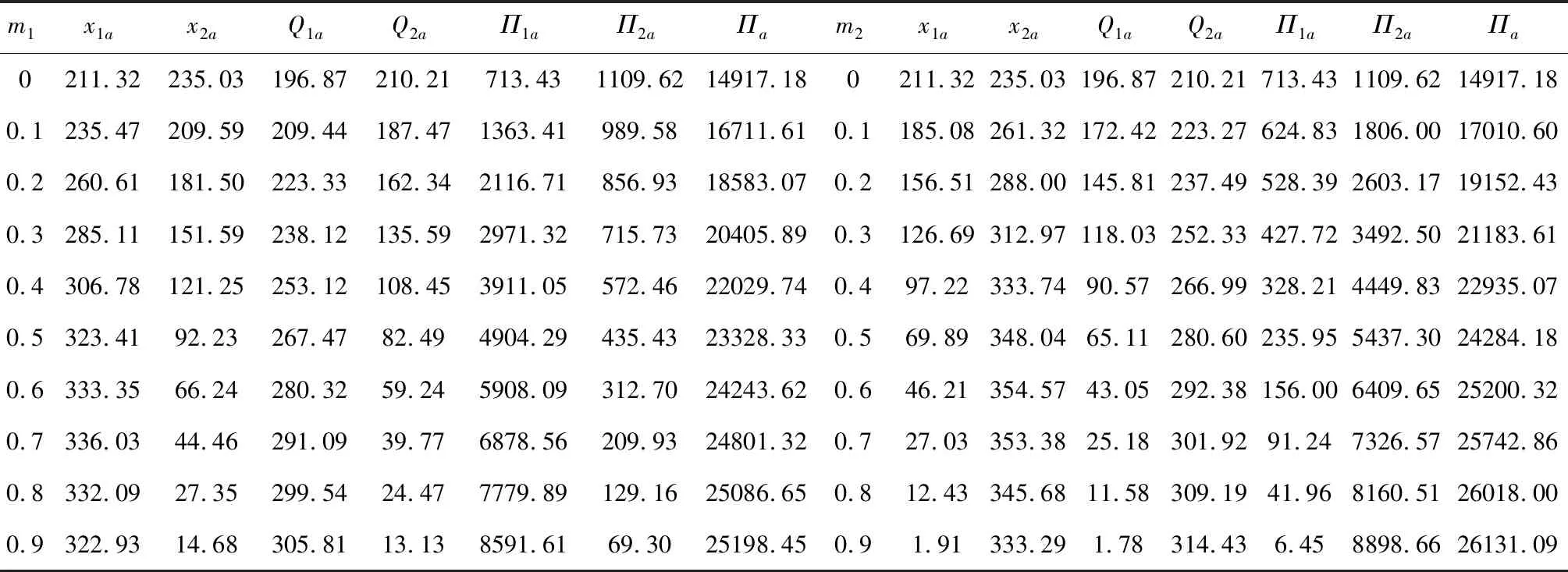
表2 供应商产出随机率对最优值的影响

(1)随着mi的增大，供应商i的生产量先增加，直到产出稳定改善(随机性降低)到一定程度(如mi=0.9)时，供应商i的生产量才减少。

(2)随着mi的增大，制造商向供应商i的订货量一直增加，向供应商j的订货量一直减少。同时发现当mi增大到一定程度时，制造商向供应商j的订货量几乎为零(如m1=0.9，Q2a=13.13;m2=0.9时，Q1a=1.78所示)。也就是说，当其中一个供应商产出稳定性改善到一定程度时，不再向另一个供应商订货，意味着另一供应商将会被淘汰。

(3)随着mi的增大，供应商i的最优期望利润在增加，供应商j的最优期望利润在减小，但制造商的最优期望利润一直在增加。

以上结论显示，供应商产出稳定性改善到一定程度时，供应商才会减少自身的生产量，在那之前，供应商在改善自身产出稳定性，降低产出随机性的同时还应该增加生产量。同时，制造商应该向不断改善产出稳定性的供应商多订货，逐渐减小未改善产出稳定性供应商的订货量，最终几乎全部向一直改善产出稳定性的供应商订货。此现象也说明，制造商在供应商产出随机时采用双源采购是为了降低风险，当风险足够低的时候，也就是其中一个供应商的产出稳定性改善到一定程度时，双源采购会被单源采购所取代。同时制造商与供应商应该合作改善供应商的产出稳定性，降低产出随机性，因为供应商产出稳定性的改善，不仅提高供应商利润，也提高制造商利润。

在供应商存在产出随机和供应中断时，同样改变两个供应商的产出随机性。按4.1节的求法，可得表3。

由表3可知，同时考虑两个供应商存在产出随机与供应中断时的各个最优决策和最优利润，与只考虑存在产出随机时的情况相同，此处的分析省略。

4.2.2 供应中断可能性对最优值的影响

以上分析了产出随机对最优值的影响，接着我们将分析供应中断可能性对最优值的影响。依次改变供应商i供应中断的可能性，随着θi的增大，供应商i的供应中断可能性降低。也按照4.1节的计算过程，代入各式可得表4。从表4中我们可以清楚的看到：

(1)无论双源采购中哪个供应商的供应中断可能性降低，制造商向两个供应商的最优订货量都在减小，但制造商的最优期望利润一直在增加。

(2)无论双源采购中哪个供应商供应中断可能性降低，两个供应商的最优生产量都在减小，供应商i的利润随供应商i供应中断可能性的降低而增加，随供应商j供应中断可能性的降低而减小。

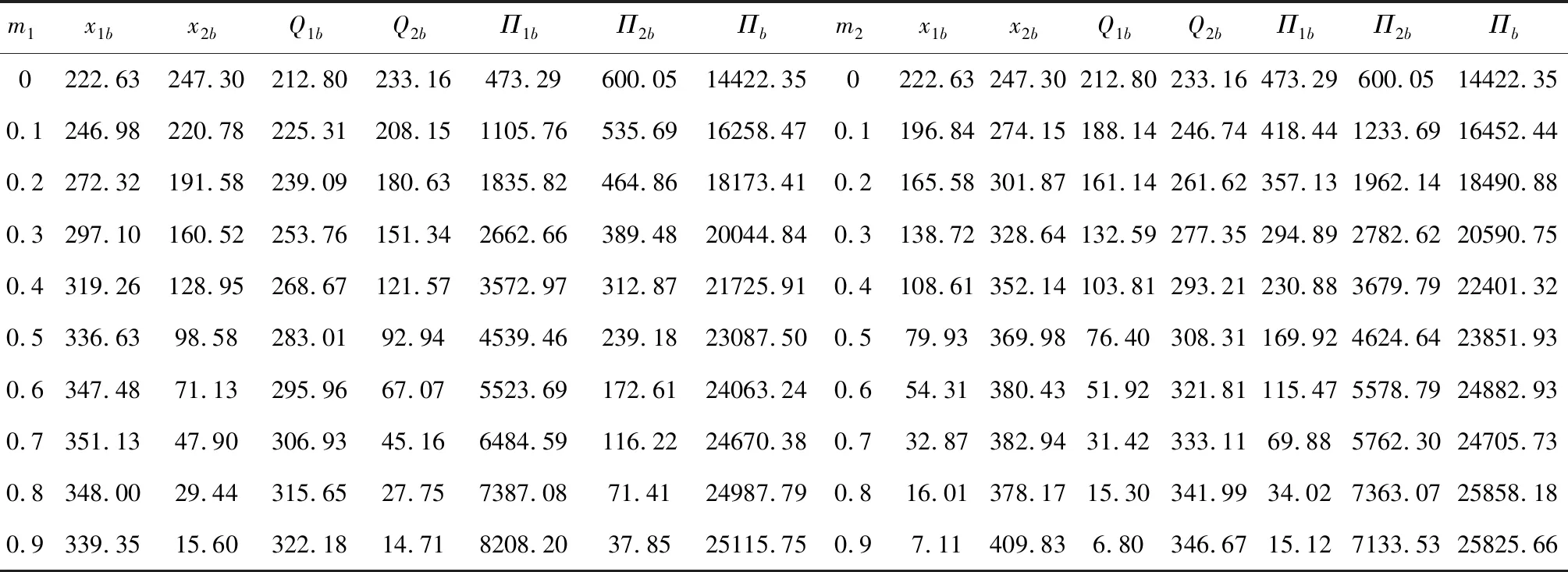
表3 风险中断时供应商产出随机率对最优值的影响

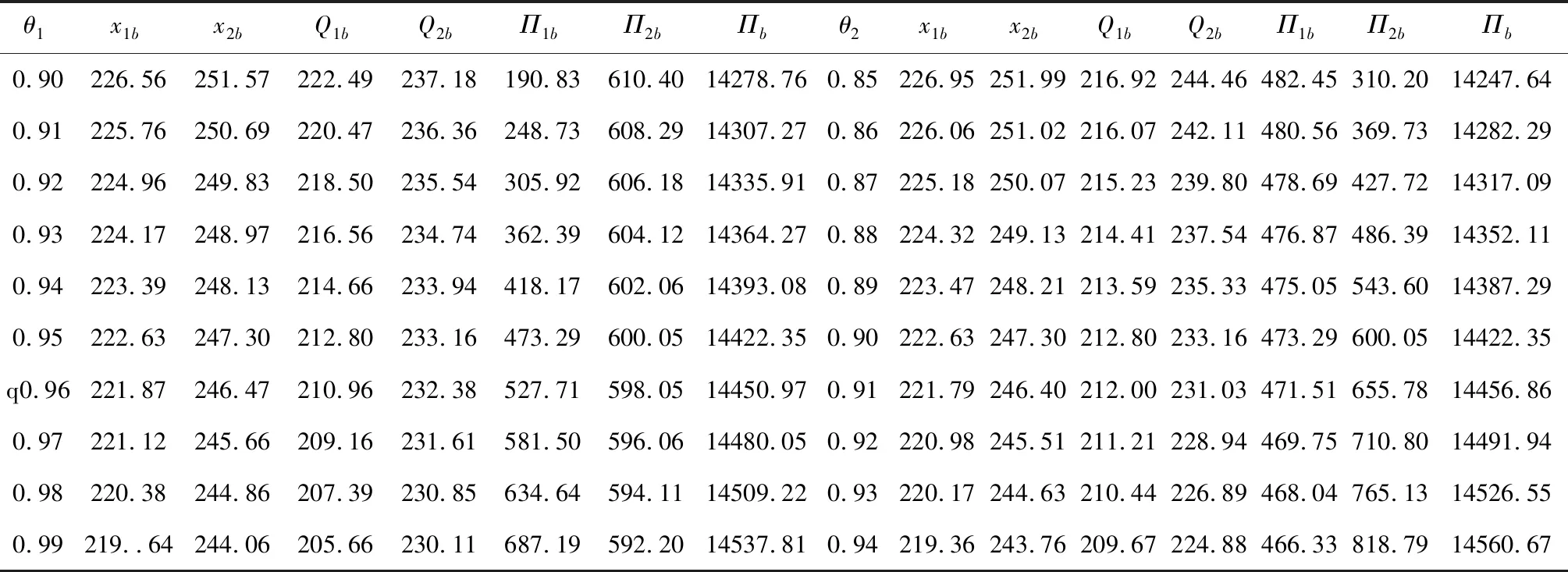
表4 供应中断可能性对最优值的影响

4.3 管理启示

由本文的理论模型和算例分析可知，供应商的产出随机不仅与供应商密切相关，还影响着制造商的利润与决策。因此在现实中，制造商在做采购决策时应该考虑这种供应不确定性对采购的影响，并准备应对措施。比如，在供应商产出率不稳定时采用双源采购，并督促供应商降低自己的产出随机性，一旦其中有供应商产出率稳定性得到很大的改善(产出随机性降低)，改善到一定程度时，制造商可以采用单源采购的形式，这也是准时化JIT采购的要求。对供应商来说，在给制造商供货的同时，应该在制造商的帮助下努力改善自己的生产与供应条件。

同时可知，在双源采购决策中，任何一个供应商供应中断概率的降低都可以增加制造商的利润水平，因此制造商在选择供应商时，应该将供应商供货中断风险作为一个重要考核因素，同时，还应该时刻关注供应商供应中断的原因，力求降低供应商供应中断的可能性。