砂土地震液化预测的GA_SVM_Adaboost模型

毛志勇，黄春娟，路世昌



砂土地震液化预测的GA_SVM_Adaboost模型

毛志勇，黄春娟，路世昌

(辽宁工程技术大学系统工程研究所，辽宁 葫芦岛 125105)

为快速准确地对砂土液化情况作出预测，选取地震烈度、地下水位、覆盖厚度、标贯击数、平均粒径、地貌单元、土质及不均匀系数为主要影响因素，运用相关性分析和因子分析模型对其进行分析和属性约减，采用遗传算法(GA)对支持向量机(SVM)的参数寻优，结合Adaboost迭代算法，建立预测砂土地震液化的GA_SVM_Adaboost模型。选用唐山地震砂土液化现场勘察资料中的329组数据对模型进行训练，利用该模型对剩余68组砂土液化数据进行预测。最后，将预测结果与GA_SVM和SVM模型预测结果进行比较。结果表明，3个模型的平均预测准确率分别为100%、98.04%、89.71%，基于因子分析的GA_SVM_Adaboost模型的预测准确性优于GA_SVM模型和SVM模型，是一种解决砂土地震液化预测问题的有效方法，具有一定的应用参考价值。

砂土地震液化；因子分析(FA)；支持向量机(SVM)；遗传算法(GA)；Adaboost算法

砂土液化是常发生于震后的具有严重危害性的一种自然灾害现象，可导致城镇、农村、桥梁、水渠、农田、道路、房屋等遭受破坏，严重影响人们的生产生活以及生命财产安全。我国是地震多发国家，地震区域分布广泛，许多重要设施处于地震液化敏感区内。因此，对砂土地震液化的理论研究和预测分析对工程抗震设计和防护具有重要的现实指导意义。

多年来，国内外学者从应用理论、现场勘测、模拟实验和仿真预测等方面对砂土地震液化问题进行了大量的研究工作[1-13]。传统方法有标准贯入法、静力触探法、剪切波速法、振动孔压触探法等，都是根据经验或规范以某个单一指标进行的砂土液化分析研究，由于砂土液化过程复杂、各影响因素间存在一定的非线性关系，这些方法均易产生误判。因此，一些学者综合考虑砂土液化影响因素，提出了多指标综合评判方法，如：文畅平等[4]基于未确知测度理论，通过建立未确知测度函数，采用相似权的赋权方法确定评价指标的权重，建立了砂土地震液化判别的未确知均值聚类分析模型和方法；张紫昭等[5]以学习样本数据的多元分布为基础，计算多元正态分布概率密度的后验概率，建立了Bayes判别函数模型；赵小敏等[6]基于Fisher判别理论，建立了砂土地震液化的FDA模型；刘章军等[7]运用模糊概率综合评判法进行砂土地震液化判别，过程中充分考虑了权重的动态性和模糊性，从而避免权重取值带来的不确定性；林志红等[8]在探讨砂土液化影响因素以及BP网络输入层模式的选择基础上，将“提前停止”算法和改进的贝叶斯正则化方法相结合建立了砂土地震液化的贝叶斯正则化的BP神经网络预测模型；赵艳林等[9]提出了一种用于砂土地震液化的灰色综合评判方法；师旭超等[10]将分类性能良好的支持向量机方法应用于砂土地震液化预测问题；薛新华等[11]根据减法聚类算法以及模糊神经网络的基本原理构造了基于减法聚类模糊神经网络的饱和砂土液化判别预测模型。上述各学者的研究均取得一定的成果，促进了砂土地震液化预测研究领域的进展，但仍然存在着影响因素之间具有较高的相关性和预测方法自身不足等，砂土地震液化预测准确性仍需进一步提高。

在信息化会计教学过程中，教学的目标和内容选择十分关键。因为只有选择合适的教学目标和内容才能有利于会计信息化的学科建设，有利于提高信息化会计教学的质量，有利于培养出适应社会需要的应用型会计人才。下面将从信息化会计教学的理论内容和实践教学内容进行探讨。

为了提高砂土地震液化预测模型的准确性，减少液化影响因素的信息冗余，笔者通过相关性分析和因子分析对砂土地震液化预测的主要影响因素进行降维，利用遗传算法(Genetic Algorithm，GA)优化支持向量机(Support Vector Machines，SVM)的惩罚参数和核参数，结合Adaboost算法训练多个GA_SVM基预测器，并通过加权集联成强预测器，建立了基于因子分析的GA_SVM_Adaboost砂土地震液化预测模型，并通过实际数据对模型的有效性进行验证。

虽然个人理财产品种类已经非常多，但是仔细比较各种理财产品可以发现，理财产品之间内容相似，储蓄、保险、基金的组合简单重复，各个理财产品之间存在非常严重的同质性问题[4-6]。这一问题一方面是由于我国相关的专业人才匮乏，创新能力差；另一方面是由于我国可供投资的金融衍生品相对匮乏，例如股指期货、期权等产品数量较少，且投资受到限制。

1 GA_SVM_Adaboost理论模型

1.1 GA_SVM分类算法

⑦转步骤③进行下一步迭代，直至迭代到第次为止。

值得注意的是，SVM模型建立过程中，不同类型核函数、核函数参数和惩罚参数的选择会对最终结果产生较大的影响，因此必须考虑此三方面的选择与优化问题。常用核函数包括线性核函数、多项式核函数、sigmoid核函数、径向基核函数等，在应用过程中发现这几种类型的核函数对SVM性能影响并不大，反而惩罚参数和核参数是SVM性能的关键影响因素。

该系统节电的软件设计沿用基于微内核操作系统的设计思路，采用模块化的设计方法，将无线通信协议、功耗管理、数据采集与处理以及外围硬件驱动等有机地集成在一起，实现信息的采集处理。

另外，GA 由美国的J. Holland教授于1975年首先提出，是一种借鉴生物界的“适者生存，优胜劣汰遗传机制”进化规律演化而来的随机化搜索方法[13]。GA 具有如下优点：

②初始化样本权重：() = 1/；= 1,2,…,；= 1,2,…,；为给定的迭代次数；()表示在第次迭代中样本的权重。

b. 目标函数和约束无论线性与否，离散连续与否都可以处理，应用较为广泛；

c. 使用概率机制进行迭代，具备快速随机的搜索能力，求出全局最优解；

d. 具有较强的鲁棒性；具备可扩展性，容易和其他算法结合等。

彭伟民最后一句话令刘丽芳无比寒心。在丈夫面前，刘丽芳一向是言听计从百依百顺，关键时候，丈夫却不肯为她做出半点让步。刘丽芳放下电话，去了卫生间。

基于上述几个优点，引入GA算法对参数和进行优化，建立GA_SVM算法模型。具体流程步骤参考文献[14]—[15]。

1.2 Adaboost算法原理

⑧输出最终的强学习器预测函数

Adaboost算法如下：

应用SPSS 17.0统计软件对数据进行统计分析。计量资料以均数±标准差(±s)表示，组间比较采用重复测量的方差分析，P＜0.05为差异有统计学意义。

①给定学习样本：(1,1)，(2,2)，…，(x,y)，其中x∈，y∈，= 1,2,…,；为训练集中样本的个数；和表示某个域或实例空间。

a. 对求解的优化问题没有过多的数学要求，搜索过程中不需要问题的内在性质；

③利用样本权重()训练弱学习器。

目前，常用来作为Adaboost算法的弱分类器有神经网络和决策树等方法，但都存在其本身的多参数及训练次数选取难的问题。若采用SVM作为Adaboost的弱分类器，便能较好地解决上述难题。对于以RBF为核函数的SVM模型，其分类性能只受惩罚参数和核参数的影响，2个参数的优化问题可以考虑采取GA算法解决，基于此，笔者构造了GA_SVM_Adaboost模型用于解决砂土地震液化预测问题，具体结构如图1所示。

⑥更新样本权重

式中Z为归一化因子，目的为在保证权重比例不变的情况下使分布权重和为1。

SVM是20世纪90年代初由Vapnic等提出的一种用于解决高维、非线性小样本问题的神经网络模型，其基本思想是利用输入空间的核函数，将低维空间下输入向量通过非线性变换映射到高维特征空间，在结构风险最小化原则和VC维理论的基础上，对有限样本进行学习训练，在解决算法可能导致的“维数灾难”问题的同时，保证获得其全局最优解，从而实现对样本数据的分类预测。SVM模型的具体计算理论详见文献[12]。

Adaboost即自适应提升算法，是Boosting算法家族的典型代表，广泛应用于分类问题。近些年来，部分学者成功将Adaboost算法拓展到回归和预测等领域[16-18]。其核心思想是：针对同一个学习样本集训练不同的弱学习器，将这些弱学习器级联起来，组合成一个更强的最终学习器，克服数据的不确定性影响，从而提高算法的预测准确度以及泛化能力。Adaboost算法在求解实际问题中取得了很好的效果。

1.3 GA_SVM_Adaboost模型流程

④获取弱学习器的预测函数h，并计算在各样本下的误差ε和平均误差ε。

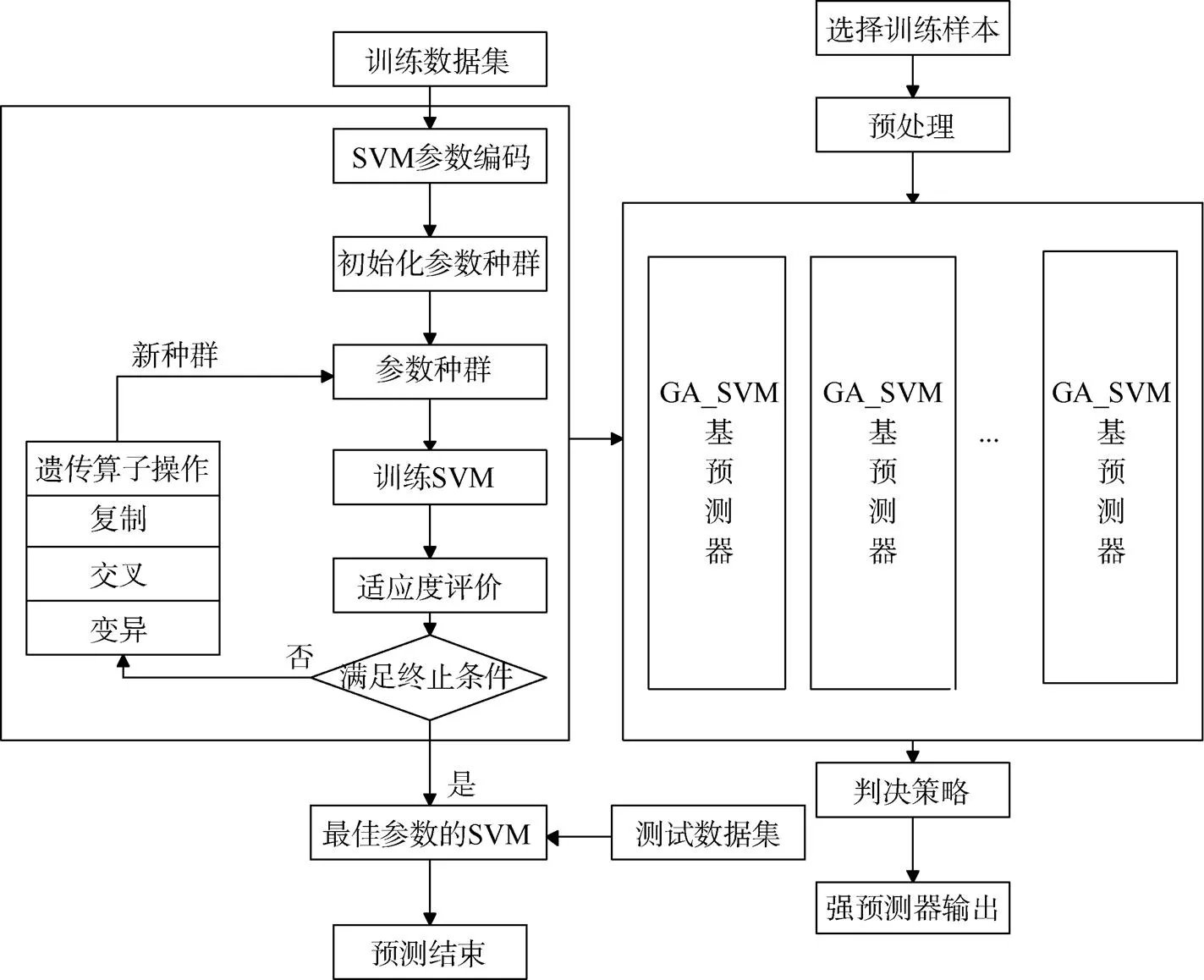
图1 GA_SVM_Adaboost模型的预测流程

2 实例分析

2.1 特征指标选取

地震所产生的砂土液化是多种因素共同作用的结果，见表1，它的发生主要受地震条件、埋藏条件及土质、地质条件等所制约。因此，在选择特征指标时应综合考虑这些因素，根据现行相关规范与条例，参照此前相关学者的学术成果[19]，本文选取地震烈度(1)、地下水位w(2)、覆盖厚度0(3)、标贯击数63.5(4)、平均粒径50(5)、地貌单元(6)、土质(7)及不均匀系数u(8)等8项指标作为砂土液化预测的初始特征指标，进行预测分析。表2为地貌单元和土质的量化。

2.2 因子分析检验

2.2.1 相关性分析

根据文献[19]所提供唐山地震砂土液化现场勘察的数据资料(表3，限于篇幅，此处只显示部分数据)，运用SPSS15.0软件对8个变量进行Spearman等级相关性分析，用以提高变量之间的相互独立性。分析结果显示：地震烈度(1)、地下水位(2)、覆盖厚度(3)、标贯击数(4)、地貌单元(6)、土质(7)及不均匀系数(8)这7个变量之间的统计量的显著性概率Sig.< 0.05，相关系数值显著异于0，表明这7个变量彼此之间存在较强相关关系，存在信息重叠；而平均粒径(5)与其他7个变量之间的统计量的显著性概率Sig.>0.05，表明该变量比较独立，与其他变量之间的相关性较弱。

表1 砂土地震液化的影响因素

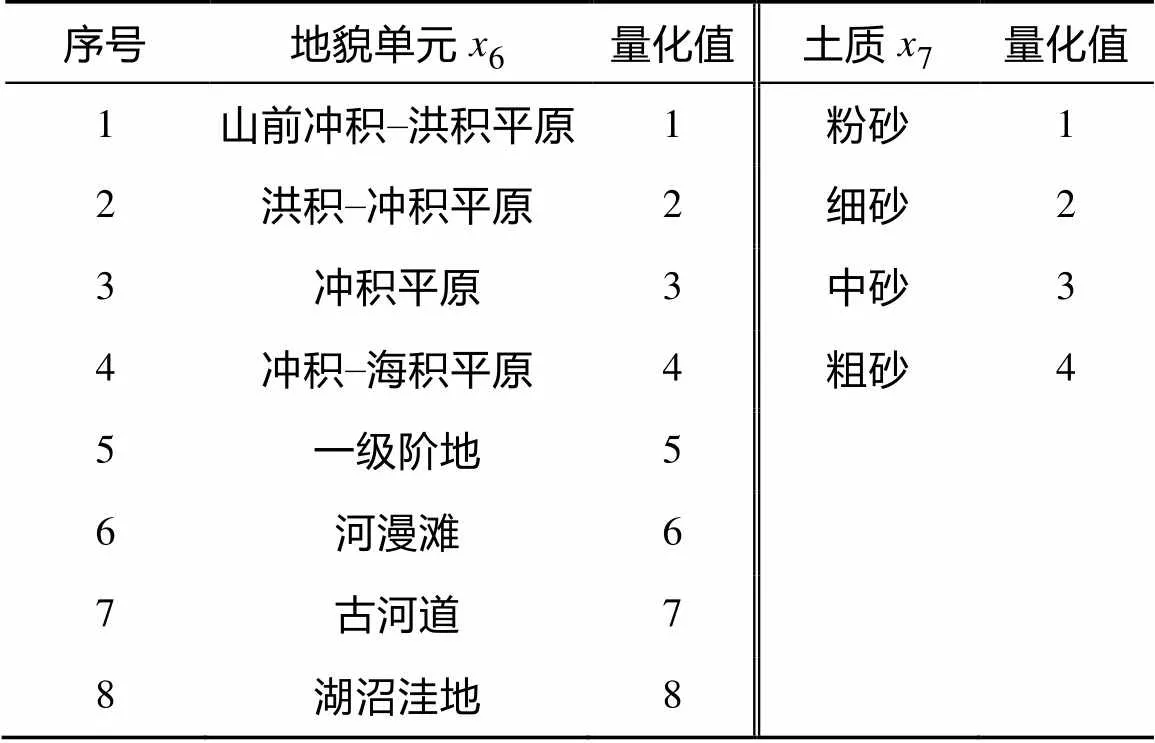
表2 指标量化表

2.2.2 因子分析的KMO和Bartlett检验

由相关性分析得到相关性较强的7个变量，变量之间存在信息冗余，直接应用于模型分析可能会造成样本误判，为了保证变量属性选取的可靠性，对这7个变量进行因子分析，约减属性。在对变量进行因子分析之前，需要先判断其是否适合进行因子分析。

运用SPSS15.0软件进行KMO和巴特莱特球形(Bartlett)检验，结果见表4，由表可知：样本的KMO值为0.654，说明这7个相关变量适合作因子分析；巴特菜特球形检验的显著性概率Sig.值为0<0.05，拒绝0假设，认为适合作因子分析。

从2014年开始，山东省财政厅组织乡镇财政业务技能竞赛，每两年一届，极大鼓励了乡镇财政人员学知识、学业务的热情。为了迎接技能竞赛，各县市区也都对各乡镇财政所所长、乡镇财政业务骨干等进行专业知识培训。培训内容丰富、重点突出，理论与实践相结合，为提升基层财政规范化、精细化管理水平，奠定坚实基础。

表3 原始样本数据(部分)

表4 样本测度和巴特莱特球形检验

根据2个检验的结果，表明了相关性较强的7个变量因素可以进行因子分析。

组织管理人员作为影响施工组织进度控制和施工管理效果的主要因素，通过对电力工程施工组织管理人员的调查，发现大部分管理人员均存在投资观念淡薄，缺乏对工程经济效益知识的了解等问题[1]。近年来，随着电力产业的快速发展，传统的电力工程施工组织进度控制和管理模式已经不适应电力工程的有效开展，尤其是在电力工程施工技术的不断创新下，电气设备的不断更新和施工工艺的创新为管理工作的开展提出了更高的要求，而受到组织管理人员专业素质较低的影响，导致许多电力工程企业均未能实现对现有施工组织进度控制和管理模式的创新。

2.3 基于因子分析的GA_SVM_Adaboost砂土地震液化预测模型

从砂土地震液化的数据中选取了397组砂土液化数据作为学习数据集，其中329组为训练样本，68组为测试样本，基于因子分析，建立GA_SVM_ Adaboost砂土地震液化预测模型。在砂土地震液化模型中，输入变量是由7个较强相关性的液化判别指标进行因子分析所提取的公共因子和较弱相关性的判别指标共同组成，输出变量为砂土液化类型：液化(1)和非液化(–1)。

运用SPSS15.0软件对7个相关变量数据进行因子分析，得到总方差解释(表5)和碎石图(图2)，以此为依据提取5个公共因子F1—F5，这5个公共因子的累积贡献率为86.734%，也就是这5个公共因子包含了原有变量指标的86.734%的信息量。

（3）模型数据传递受阻。BIM技术最为显著的特点便是信息的传递与组合，使设计和施工达到无缝衔接的目标。在装配式建筑设计中，为了便于单个预制构件的出图与工程量统计，通常会对项目中的构件进行拆分，并通过链接的形式拼装起来，但Revit软件并无文件信息提取功能，使整个建筑中模型数据的顺利传输受到极大阻碍[2]。

表5 总方差解释表

图2 碎石图

将较弱相关性的单个指标(平均粒径)和5个公共因子作为GA_SVM_Adaboost预测模型的输入，在MATLAB R2014bR软件平台进行编程训练。由于数据的数量级存在较大差异，数据尺度不统一，因此对转化后的数据进行归一化处理。在Matlab运行程序中，调用premnmx( )函数对数据进行归一化处理。

三是大力发展民生水利，着力提高水利公共服务能力。完成17处大型灌区和9处中型灌区年度节水改造任务，实施好6个规模化节水灌溉增效示范项目建设，建设节水灌溉面积510万亩（34万hm2）、“旱能浇、涝能排”高标准农田385万亩（25.67万hm2）。解决360万人饮水安全问题，推进沿黄地区饮水安全平原水库建设，建立县级水质检测中心和供水服务“116”热线。

当前PPD发病率正逐年增加，临床上主要表现有悲伤、落泪、情绪不稳定、睡眠障碍等。临床上往往需要针对患病的神经衰弱、抑郁症及神经官能症等进行对症治疗，但是后期效果不佳，虽然新的抗抑郁药物不断出现，但是多数价格昂贵，且存在较多不良反应，哺乳期妇女服用这类药物可能会有损婴儿健康，因此，PPD的治疗成为业界人士研究的重点课题之一。

采用GA算法优化SVM的惩罚参数和核参数，用GA_SVM基预测器对输入输出值进行训练，然后运用Adaboost算法多次训练GA_SVM，对多个GA_SVM基分类器加权组合形成强预测器。其中的模型参数设定：、的取值范围为：∈(0,100)，∈(0,1 000)；种群个数为 20，最大进化代数取 50，交叉和变异概率分别为 0.7 和 0.05；基预测器的个数=10。

在用GA_SVM_Adaboost模型进行优化训练的同时，也训练出了GA_SVM、SVM预测模型。3种方法分别进行3次仿真实验，所得到的预测准确率如表6所示。可以看出：GA_SVM模型对砂土液化类型都存在着一定误判，但GA_SVM对SVM预测结果有着显著的优化效果，提高了SVM单一模型的预测准确性。而由预测准确性较高的GA_SVM作为基预测器所形成的GA_SVM_Adaboost强预测器，其预测准确率达到100%，为砂土地震液化预测提供了一种更为高效稳定的预测方法。

表6 测试数据的预测准确率结果

3 结论

a. 应用相关性分析和因子分析法对砂土地震液化的影响因素进行特征提取，消除了因素之间的冗余信息，在降低模型复杂度的同时，有效提高了模型的预测准确性。

b. 在砂土地震液化预测中，GA_SVM_Ada­boost模型具有较好的稳定性和极高的准确率，且预测效果明显优于GA_SVM和SVM 2个模型，可以进一步提高砂土地震液化预测的准确性。

c. 基于因子分析的GA_SVM_Adaboost砂土地震液化预测模型只是笔者的初步尝试。在特征选取过程中，未能全面地考虑砂土液化影响因素，而是选取了几个具有代表性和易取性的因素，对于可能存在的重要因素有待后续工作的开展。另外，文中数据来源于唐山地震周边区域的信息采集，而世界各地的地震条件、埋藏条件和土、地质条件等却异于唐山地区，因此该问题在后期研究过程中有待探究。

[1] JUANG C H，ROSOWSKY D V，TANG W H. Reliability-based method for assessing liquefaction potential of soils[J]. Journal of Geotechnical and Geoenvironmental Engineering，1999，125(8)：684–689.

[2] RAHMAN M S，WANG Jun. Fuzzy neural network models for liquefaction prediction[J]. Soil Dynamics and Earthquake Engineering，2002，22(8)：685–694.

[3] 潘建平，曾庆筠，宋应潞，等. 尾矿坝地震液化侧向位移分析方法及应用[J]. 中国安全科学学报，2015，25(12)：99–104.PAN Jianping，ZENG Qingyun，SONG Yinglu，et al. An analysis method of seismic liquefaction-induced lateral displacement for tailings dam and its application[J]. China Safety Science Journal，2015，25(12)：99–104.

[4] 文畅平，陈宗辉，孙政，等. 基于未确知均值聚类分析的砂土地震液化评价[J]. 地下空间与工程学报，2017，13(2)：517–524.WEN Changping，CHEN Zonghui，SUN Zheng，et al. Assessment of sandy soil liquefaction potential based on unascertained average clustering method[J]. Chinese Journal of Underground Space and Engineering，2017，13(2)：517–524.

[5] 张紫昭，陈巨鹏，陈凯，等. 砂土地震液化预测的Bayes判别模型及其应用[J]. 桂林理工大学学报，2014，34(1)：63–67.ZHANG Zizhao，CHEN Jupeng，CHEN Kai，et al. Bayes discriminant analysis model for seismic sand liquefaction[J]. Journal of Guilin University of Technology，2014，34(1)：63–67.

[6] 赵小敏，曹丽文. 砂土液化预测的Fisher判别分析模型及应用[J]. 水文地质工程地质，2012，39(3)：129–133.ZHAO Xiaomin，CAO Liwen. Fisher discriminant analysis model and its application to sand liquefaction prediction[J]. Hydrogeology & Engineering Geology，2012，39(3)：129–133.

[7] 刘章军，叶燎原，彭刚. 砂土地震液化的模糊概率评判方法[J]. 岩土力学，2008，29(4)：876–880.LIU Zhangjun，YE Liaoyuan，PENG Gang. Fuzzy probability comprehensive evaluation method for sand liquefaction during earthquake[J]. Rock and Soil Mechanics，2008，29(4)：876–880.

[8] 林志红，项伟. 基于贝叶斯正则化BP神经网络的砂土地震液化研究[J]. 安全与环境工程，2011，18(2)：23–27.LIN Zhihong，XIANG Wei. Analysis on sand seismic liquefaction by bayesian regulated BP-neural networks[J]. Safety and Environmental Engineering，2011，18(2)：23–27.

[9] 赵艳林，杨绿峰，吴敏哲. 砂土液化的灰色综合评判[J]. 自然灾害学报，2000，9(1)：72–79.ZHAO Yanlin，YANG Lyufeng，WU Minzhe. Grey synthetic evaluation of liquefaction of sands[J]. Journal of Natural Disasters，2000，9(1)：72–79.

[10] 师旭超，郭志涛，韩阳. 基于支持向量机的砂土液化预测分析[J].西北地震学报，2009，31(4)：363–366.SHI Xuchao，GUO Zhitao，HAN Yang. Analysis on sand seismic liquefaction prediction based on the support vector machine[J]. Northwestern Seismological Journal，2009，31(4)：363–366.

[11] 薛新华，杨兴国. 基于减法聚类模糊神经网络的砂土液化势判别[J]. 地震工程与工程振动，2012，32(2)：172–177.XUE Xinhua，YANG Xingguo. Analysis of sand liquefaction potential of sand based on subtractive fuzzy neural network[J]. Journal of Earthquake Engineering and Engineering Vibration，2012，32(2)：172–177.

[12] 邵良杉，李永利，赵琳琳. 露天采矿爆破振动对民房破坏的SVM预测模型[J]. 中国安全科学学报，2013，23(9)：26–32.SHAO Liangshan，LI Yongli，ZHAO Linlin. SVM model for predicting residential house’s damage from blasting vibration of open pit mining[J]. China Safety Science Journal，2013，23(9)：26–32.

[13] 赵涛，于师建. 基于GA-BP神经网络算法的高密度电法非线性反演[J]. 煤田地质与勘探，2017，45(2)：147–151.ZHAO Tao，YU Shijian. GA-BP neural network algorithm-based nonlinear inversion for high density resistivity method[J]. Coal Geology & Exploration，2017，45(2)：147–151.

[14] 袁志刚，王宏图，胡国忠，等. 立井井筒非采动破裂的遗传–支持向量机预测模型[J]. 煤炭学报，2011，36(3)：393–397.YUAN Zhigang，WANG Hongtu，HU Guozhong，et al. Forecast model of GA-SVM for shaft-lining non-mining fracture[J]. Journal of China Coal Society，2011，36(3)：393–397.

[15] 乔美英，程鹏飞，刘震震. 基于GA-SVM的矿井涌水量预测[J]. 煤田地质与勘探，2017，45(6)：117–122.QIAO Meiying，CHENG Pengfei，LIU Zhenzhen. Mine water inflow prediction based on GA-SVM[J]. Coal Geology & Exploration，2017，45(6)：117–122.

[16] 王改革，郭立红，段红，等. 基于Elman_AdaBoost强预测器的目标威胁评估模型及算法[J]. 电子学报，2012，40(5)：901–906.WANG Gaige，GUO Lihong，DUAN Hong，et al. The model and algorithm for the target threat assessment based on Elman- AdaBoost strong predictor[J]. Acta Electronica Sinica，2012，40(5)：901–906.

[17] 李松，解永乐，王文旭. AdaBoost_BP神经网络在铁路货运量预测中的应用[J]. 计算机工程与应用，2012，48(6)：233–234.LI Song，XIE Yongle，WANG Wenxu. Application of AdaBoost_BP neural network in prediction of railway freight volumes[J]. Computer Engineering and Applications，2012，48 (6)：233–234.

[18] 李翔，朱全银. 基于Adaboost算法和BP神经网络的税收预测[J]. 计算机应用，2012，32(12)：3558–3560.LI Xiang，ZHU Quanyin. Tax forecasting based on Adaboost algorithm and BP neural network[J]. Journal of Computer Applications，2012，32 (12)：3558–3560.

[19] 唐山地震砂土液化联合研究小组. 唐山地震砂土液化现场勘察资料研究报告[R]. 北京：北京市勘察处，1983：26–41.

GA_SVM_Adaboost model for prediction of earthquake-induced sandy soil liquefaction

MAO Zhiyong, HUANG Chunjuan, LU Shichang

(System Engineering Institute, Liaoning Technical University, Huludao 125105, China)

In order to predict the liquefaction of sand, the seismic intensity, groundwater level, covering thickness, standard number, average particle size, landform, soil quality and inhomogeneity coefficient are selected as influencing factors. Genetic algorithm(GA) is used to optimize the parameters of support vector machine(SVM) by using correlation analysis and factor analysis model, and combining with Adaboost iterative algorithm, the GA_SVM_ Adaboost model for predicting the liquefaction of sand is established. 329 sets of survey data of sandy liquefaction site in Tangshan earthquake were used to train the model, and 68 samples of sandy liquefaction data were predicted by using the good model. Finally, The predicted results are compared with that of GA_SVM model and SVM model. The results show that the average prediction accuracy of three models is 100%, 98.04% and 89.71% respectively. The GA_SVM_Adaboost model based on factor analysis is better than GA_SVM model and SVM model which could improve the prediction accuracy. It is an effective method to predict the liquefaction of earthquakes.

earthquake-induced liquefaction of sandy soil; factor analysis(FA); support vector machines(SVM); genetic algorithm(GA); adaboost algorithm

National Natural Science Foundation of China(70971059)

毛志勇，1976年生，男，陕西汉中人，博士，副教授，从事数据挖掘、信息系统及系统工程等方面的研究. E-mail：405949570@qq.com

毛志勇，黄春娟，路世昌. 砂土地震液化预测的GA_SVM_Adaboost模型[J]. 煤田地质与勘探，2019，47(3)：166–171.

MAO Zhiyong，HUANG Chunjuan，LU Shichang. GA_SVM_Adaboost model for prediction of earthquake-induced sandy soil liquefaction[J]. Coal Geology & Exploration，2019，47(3)：166–171.

1001-1986(2019)03-0166-06

TU441.4

A

10.3969/j.issn.1001-1986.2019.03.026

2018-04-15

国家自然科学基金项目(70971059)

(责任编辑 张宏 周建军)