基于声压的无损检测方法研究

张亚建　毛虎平　程意　王瀚岑　李煜华

摘要：为实现工业生产流水线产品的快速无损检测，结合结构动力学理论和声辐射模态理论，论述声辐射模态频率作为无损检测依据的可行性，提出一套基于声压的无损检测方案。该方案结合使用Matlab和高精度麦克风、工业声卡等硬件设备实现声音信号采集、FFT变换和模态识别等功能。以长安CS55发动机连杆为例进行试验，结果与Ansys仿真结果对比验证此试验方案的准确性。最后对上述连杆进行无损检测，通过对大量连杆进行重复试验的结果对比发现：利用声压的无损检测方案可以成功检测缺陷连杆，而且检测结果较为稳定。

关键词：声压;无损检测;模态;连杆;缺陷

中图分类号：TG247 文献标志码：A 文章编号：1674-5124（2019）01-0008-06

0 引言

随着工业生产的发展，将基于声压的无损检测方法应用于工业流水线产品检测已经成为一种趋势。利用声压的无损检测方法是以声辐射模态理论和结构动力学理论为基础，旨在用声辐射模态频率为识别依据，进行非接触式无损检测。自1990年，Borgiotti[1]首次提出声音辐射模态的概念，学者们对声辐射模态进行了大量的研究，Williams等[2-3]通过声压测量阵列来实现结构表面振动响应的重建，但其尚未对结构的模态进行分析;赵坚等[4]结合模态理论对结构振动与声辐射关系进行研究，从理论上证明了振动模态与声压模态与之间的关系;郭建平等[5]在上述理论基础上使用声压传感器对某电路板的模态参数成功识别;Prezelj等[6]利用表面近场的测量声压实现了振动结构模态重构，证明近场声压模态反应结构模态更加准确;Zhu等[7-8]使用有限元方法建立声固耦合的动力学方程，验证了利用声压识别结构模态的可行性。夏茂龙等[9]建立辐射声压与激振力之间的声压频响函数矩阵，提出一个基于测量声音识别结构模态参数的新方法。

上述研究表明利用声压信号进行模态识别的技术已趋于完善。由于模态参数可以作为无损检测的依据[10]，刘广兴等[11]提出了一种仅用计算机就可以实现的快速简易无损检测新方法，由于该方法使用计算机自带麦克风和声卡而且尚未进行严格的仿真验证，未能实现精确的无损检测;王杨川[12]提出了一套基于共振声学的无损检测新思路，包括零件响应、采集声压信号、FFT变换和结果分析的4步走检测方案，但尚未进行试验验证。

综上所述，雖然利用声压信号进行模态识别的技术已趋于成熟，将这种非接触式模态识别方法应用到精确的无损检测的案例并不多。本文在前人的基础上提出了一种结合Matlab软件以及高精度麦克风、工业声卡等硬件设备的更加精确的无损检测方案，并且以长安CS55发动机连杆为例进行了实例验证。

1 理论依据

结构动力学理论中指出任意物理对象都可以用质量、刚度、阻尼等系列物理参数构成的力学微分方程来描述[13]，对于如图1所示单自由度系统满足：

mx″（t）+cx′（t）+kx（t）=F（t）（1）

对于无阻尼系统：

对于多自由系统，式（2）也成立。由于机构模态频率由其刚度和质量共同决定，含缺陷机构的刚度和质量发生变化导致其模态频率改变，通过模态分析，依据频率参数就可以将缺陷零件进行筛选，这就是结构动力学理论在无损检测中最核心的应用。

声辐射模态理论是研究结构在主振动（模态振动）下声辐射特性的问题，反映了声辐射特性和振动结构固有模态之间的关系，论证用声辐射模态参数表述结构声辐射固有特性的合理性[14]。

根据声学理论，对于稳态单频率k振动，结构声辐射面是封闭光滑曲面（或分片光滑曲面）s，满足有限条件和辐射条件的情况下，设曲面s上的法向振速分布函数u（x，t），由格林函数方法可建立辐射面s上的Helmholtz积分方程：其中P（x，t），P（y，t）分别为辐射面x，y点的声压分布函数;为格林函数，K=k/c为波数，c为波速，r=r（x，x）表示s面上任意两点x和y之间的距离;为法向导数。

对于镶在无穷大障板上的平板单元结构向半空间辐射噪声，可由式（3）导出声学瑞利（Rayleigh）积分公式为

根据式（4）可知，当结构以某阶模态频率发生主振动时，辐射面辐射的声学量将以相同的频率进行变化，因此可以通过声学量信号频率来确定结构模态频率，这与文献[15]用加速度传感器和声压传感器测得结构模态频率几乎相同的结论相一致。本文基于以上理论来进行无损检测。

2 声压模态测试方案

本文设计的测试方案如图2所示，首先将力锤拉起至与垂线成固定角度位置，松手使其绕与量角器同心轴自由下摆，近似地实现了对机构的固定位置固定力激励，零件受到激励产生一定的声音信号，通过固定在待测机构正下方的麦克风进行声音信号采集，通过声卡将声音信号转化为数字信号输人到电脑，最后使用Matlab对数字信号FFT变换[16]，得出待测零件的固有频率。

2.1 测试设备和流程

本测试方案所需设备及选型如表1所示。

本试验以长安CS55发动机连杆为例进行测试，根据此连杆有限元仿真结果可得最大振幅位置在连杆小头，所以选择小头为本试验的激励位置，中间的振幅较小，选择中间为悬挂位置，至于测试位置选择距离敲击点正下方1cm处，试验实物图如图3所示。

测试分析过程如下：

1）将力锤向右拉起与水平线成20°夹角位置松手，锤头自由摆动激励连杆，连杆受到激励后自由震动。由于橡胶锤头消耗重力势能，所以可以通过选择硬度不同的锤头来避免自由摆动锤头的重复敲击连杆。

2）连杆自由振动发声，声音信号经空气、麦克风和声卡传输到电脑。声音信号在空气中传递时会衰减，由于测量位置距离激励位置非常近，所以此因素仅影响频谱图峰值的大小，而峰值频率（共振峰值对应的横坐标）位置不会改变。

3）电脑收到信号，在Matlab中进行FFT变换处理，将时域信号转化为频域信号，并且显示频谱图，在频谱图中就可以直观地读取连杆各阶固有频率。

2.2 测试结果

以长安CS55发动机连杆为例通过上述声压模态试验，得到频谱图如图4所示。

由图可得此连杆前6阶的固有频率分别是：2035，2286，3468，6306，8580，9049Hz。

3 仿真验证

为验证上述声压模态试验的可行性，进行有限元仿真验证。首先利用三维扫描仪对上述连杆进行三维扫描，将点云导入CAITA进行逆向建模，建模过程中对于比较难测量连杆的纹理进行简化，连杆逆向建模结果如图5所示。

将图5模型导入Ansys进行有限元仿真。长安CS55发动机连杆所用的材料为40Cr，其密度7870kg/m³，弹性模量2.11e¹¹N/m²，泊松比0.277。网格划分要首先考虑的是如何划分连杆模型使其达到网格数量的最优化。连杆模型是三维模型，因此本文尝试了solid185、solid187以及solid92等多个实体单元，设置了从0.001m到0.01m梯度尺寸划分网格，分别进行仿真计算。当采用solid185单元，尺寸设置为0.02m时计算结果收敛，solid185单元是六面体单元，此时划分网格后的连杆模型有52330个单元，12306个节點。建立的有限元模型，如图6所示。

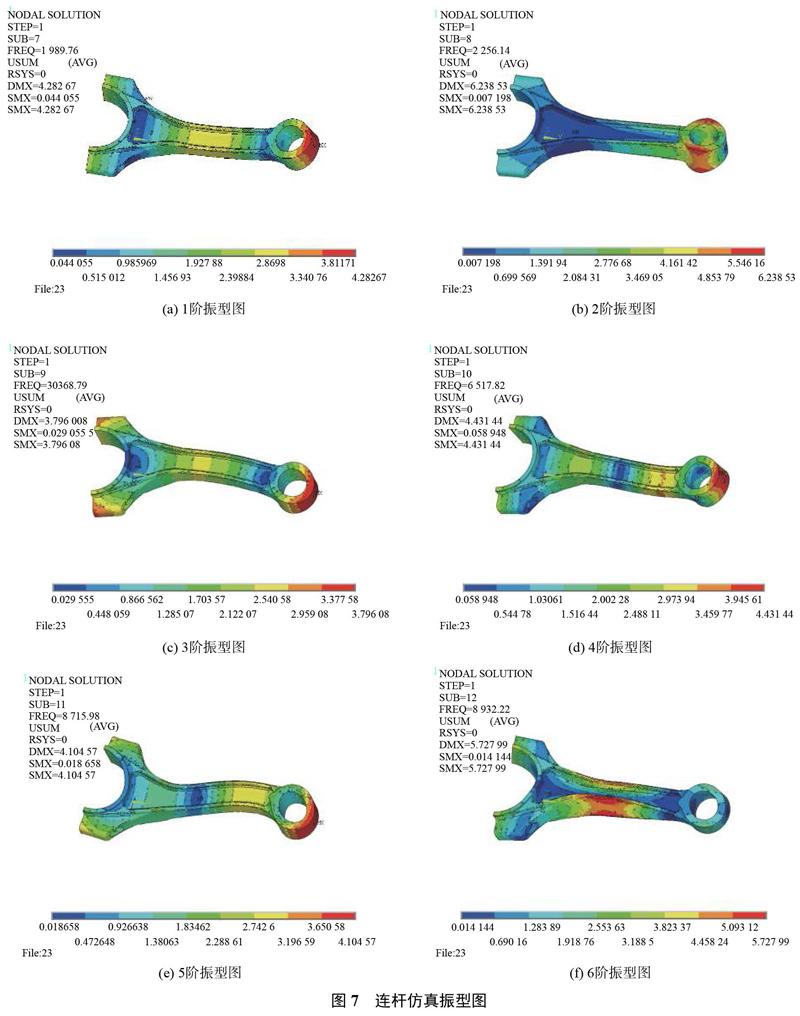
本仿真模拟的是自由模态，所以无需设置边界条件和施加载荷，采用block lanczos模态提取方法计算前6阶有效模态分别是1990，2256，3369，6218，8716，8932Hz，对应前6阶振型图如图7所示。

根据图7可得，此连杆除第6阶以外，其前5阶的最大振动位置全部在连杆小头，而第1阶、第2阶和第6阶的最小振动位置全部在杆身和小头大头连接部位，这为上述声压模态试验激励位置选择提供的参考。将声压模态试验与有限元仿真的前6阶的模态结果对比如表2所示。

上述结果表明基于声压测试连杆模态频率误差不超过士3%，由于仿真过程中逆向建模和有限元模型建立也都存在一定误差，所以近似认为此测试方案可以有效测试连杆模态频率。

4 声压模态在无损检测领域的应用

国内外常见无损检测方法有射线检测、超声检测、液体渗透检测、涡流检测、磁粉检测，以上检测技术往往旨在诊断零件的某种特定缺陷，但相比本文提出的声压模态无损检测方法，其主要缺点如表3所示。

实际上，在工业生产的流水线上，找出有缺陷次品的意义已经大于对零件某缺陷的诊断。声压模态无损检测方法是以声辐射模态参数为依据进行缺陷识别，相比以上5种检测技术检测门槛底、对人无伤害并且可批量检测。本文以长安CS55发动机连杆进行为例进行此无损检测方案可行性的验证。

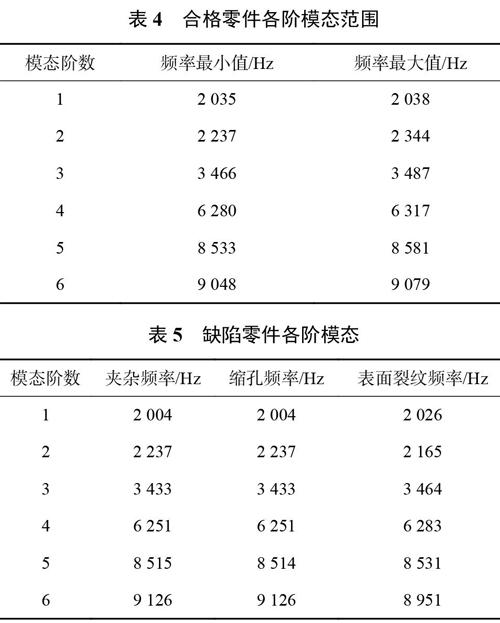
为保证无损检测的准确性，使用了100个合格连杆和3个不合格连杆作对比试验，3个不合格连杆缺陷分别是表面裂纹、夹杂和缩孔3种常见加工缺陷。100个合格连杆重复试验所得前6阶固有频率范围如表4所示，3个不合格连杆试验结果如表5所示。

对比表4、表5可得，夹杂连杆的第1阶、第3阶、第4阶以及第5阶的频率明显变小，实际上夹杂连杆刚度不足，这与式（2）反映的刚度减小导致固有频率减小的理论相一致，缩孔连杆各阶频率与夹杂连杆频率类似，表面裂纹连杆除第4阶以外其他各阶频率也有所减小，但减小值不明显。虽然上述3种缺陷对连杆各阶频率影响不相同，但与合格连杆模态试验模型库对比，存在裂纹、夹杂、缩孔的连杆固有频率多数都有所降低。因此，通过共振频率的对比可判断出连杆是否存在缺陷。

5 结束语

本文依据结构动力学理论和声辐射模态理论提出了一套基于声压的无损检测新方案，方案利用工业声卡、高精度麦克风和Matlab软件等设备，操作方法简单、硬件成本低、识别快速，并且使用Ansys仿真验证了此方案测试模态参数的准确性。之后将此方案应用到长安CS55发动机连杆的无损检测试验，验证了其可行性。由于本文仅使用了发动机连杆为例，发动机连杆是锻造件，锻造产生的缺陷比较明显，而对于其他加工工艺零件尚未进行无损检测的验证，因此对此无损检测方案有待更进一步研究和推广。

参考文献

[1]BORGIOTTI G V.The power radiated by a vibrating body inan acoustic fluid and its determination from boundarymeasurements[J].Journal of the Acoustical Society ofAmerica，1990，88（4）：1884-1893.

[2]WILLIAMS E G.Regularization methods for near-fieldacoustical holography[J].Journal of the Acoustical Society ofAmerica;2001，110（4）：1976-88.

[3]李双，陈克安，潘浩然.基于模态理论的有源声学结构控制机理研究[J].振动工程学报，2007，20（2）：140-144.

[4]赵坚，于明.航空发动机涡轮盘振动模态与声模态分析研究[J].兵工学报，2010（S1）：179-183.

[5]郭建平，杨洁，杨明明，等.基于声压传感器的电路板试验模态分析[J].机械工程师，2012（6）：81-83.

[6]PREZELJ J，LIPAR P，BELSAK A，et al.On acoustic verynear field measurements[J].Mechanical Systems&SignalProcessing，2013，40（1）：194-207.

[7]ZHU W D，LIU J M，XU Y F，et al.A modal test methodusing sound pressure transducers based on vibro-acousticreciprocity[J].Journal of Sound Vibration;2014，333（13）：2728-2742.

[8]PIERRO E，MUCCHI E，SORIA L，et al.On the vibro-acoustical operational modal analysis of a helicopter cabin[J].Mechanical Systems&Signal Processing，2009，23（4）：1205-1217.

[9]夏茂龙，黎胜.基于声压测量的结构模态参数辨识[J].振动与冲击，2017，36（22）：232-238.

[10]万小朋，王军强，赵美英.基于模态频率和神经网络的结构损伤检测[J].西北工业大学学报，2003，21（2）：156-159.

[11]刘广兴，李大勇，王利华，等.基于计算机声卡和MATLAB的铸件缺陷音频检测技术[J].铸造设备与工艺，2008（1）：18-21.

[12]王杨川.基于共振声学原理的快速无损检测系统研究[J].工业，2016（5）：236.

[13]傅志方，华宏星.模态分析理论与应用[M].上海：上海交通大学出版社，2000：76-78

[14]仪垂杰，杜树才.结构振动模态声辐射理论及试验研究[J].长春工业大学学报（自然科学版），1990（6）：28-37.

[15]刘文峰，应怀樵，李俊宝，等.通过声音识别平板结构模态的测试方法研究[C]//2000年全国振动（诊断、模态、噪声）技术及工程应用学术会议，2000.

[16]于振江.一种基于Matlab的语音信号采集与分析系统设计[J].图书情报导刊，2012，22（12）：112-114.