货币时间价值原理在运用过程中易错点的分析

王朝辉 王娟

摘要：在企业的财务估价及投资决策中，货币时间价值的运用具有至关重要的作用，若运用不好货币时间价值，就无法准确地对企业进行估价及投资决策，就无法学好财务管理。因此，通过总结学生在货币时间价值运用中的易错点，对其原因进行分析后，通过图的形式展开了分析，以帮助学生更好地理解运用。

关键词：货币时间价值;年金;现金流量分布图;复利

基金项目：广东省特色重点培育学科-会计学学科（编号：粤教研函[2017]1号，重点培育序号11）;广东海洋大学寸金学院2018年度创新强校工程项目：管理会计应用型人才培养新机制的研究和实践（编号：CJ18CXQX003）

本文将学生在运用货币时间价值时的易错点进行归纳，比如现金流量分布图的描绘;预付年金和普通年金关系的转换以及递延年金方法的运用。基于此，本文以图的形式展开了相应的分析，由于图比较直观易懂且不像公式推导那样过程烦琐，从而可以帮助学生更好的理解货币时间价值，更好地学好财务管理。

1.现金流量分布图的描绘

部分学生在学习货币时间价值时，对于各对应时点发生的现金流的确定不够准确。原因在于，学生在学习时将自己置身于一个被动的学习状态，没有结合生活常识进行学习。在画现金流量图时部分同学是以1为起点进行，如图1所示，这样的话在确定现金流发生的时点是很容易弄错。

而实际在画现金流量分布图时，应结合分析的时间来进行，有多少年就要画多少条线段，因为一年的时间是不能单独用一个点进行表示，而应该用区间进行表示。如图2所示，相对于时间段的现金流量对应的时点在流量分布图中的第一年年初始终用0表示，后续各数字分别代表各年的年末。上一线段的终点与下一线段的起点相重叠，表示一年末紧接着下一年年初。再结合所发生的收付款项对应的时点后即可准确画出现金流量分布图了。

2.预付年金与普通年金的关系

年金只要符号三个条件：間隔相同时期、金额相等、收付款项大于等于2期即属于年金。由于年金发生时点不同会有普通、预付、永续及递延年金之分，都同属于年金形式，所以在分析预付年金时，预付年金的系数都是通过普通年金转换得到的。在进行这部分学习时，学生常出现的问题是：预付和普通年金无法准确地区分，求解时经常会弄错。

（1）预付和普通年金区分时，主要关注收付款项是在相应时间经过以后发生，还是经过之前发生。如果是经过以后发生的，为后付年金，又因为在实践中普遍存在也称为普通年金;如果是经过之前发生的，则称之为先付年金或预付年金。在学习时如果通过公式去进行转换，给文科的学生一种很难的直视感。所以此处通过图的形式来进行转换，比较直观、通俗易懂。

（2）预付年金终值。在学习图3普通年金以后，得知FA=A×（F/A，i，n），通过以符号形式表述时，FA为n期普通年金的终值，A为年金，（F/A，i，n）为普通年金终值系数。

当涉及如图4所示的n期预付年金求终值时，我们通过转换普通年金终值系数求预付年金终值系数。

如求图4的n期预付年金终值时。我们通过在0前面延长一期，在n对应的时点假设存在一个收付款项A（前面延长一期对求终值无影响）（如图5）。则图4的n期预付，则转换成了n+1期的普通年金，在n时点时FA=A×（F/A，i，n+1），因为假设在n时点有一个A，而实际并没有。所以总体应减一个A，则n期预付年金终值FA=A×[（F/A，i，n+1）-1]。n期预付年金终值系数[（F/A，i，n+1）-1]是在n+1期普通年金终值系数值减1。

此外，求解图4预付年金终值时，我们也可以只在0时点前面延长一期，则从0到n-1这时间段，则为n期的普通年金的形式，Fn-1=A×（F/A，i，n），又因为图4是求n对应时点的预付年金终值，还需在Fn-1的基础上再复利一期到n期（如图6所示）。则FA=A×（F/A，i，n）×（1+i），则n期预付年金终值系数（F/A，i，n）×（1+i）是在n期普通年金终值系数值的基础上乘以（1+i）。

（3）预付年金现值。通过学习图7的普通年金现值，得PA=A×（P/A，i，n），其中，PA为n

（4）普通年金的现值，A为年金，（P/A，i，n）为普通年金现值系数。

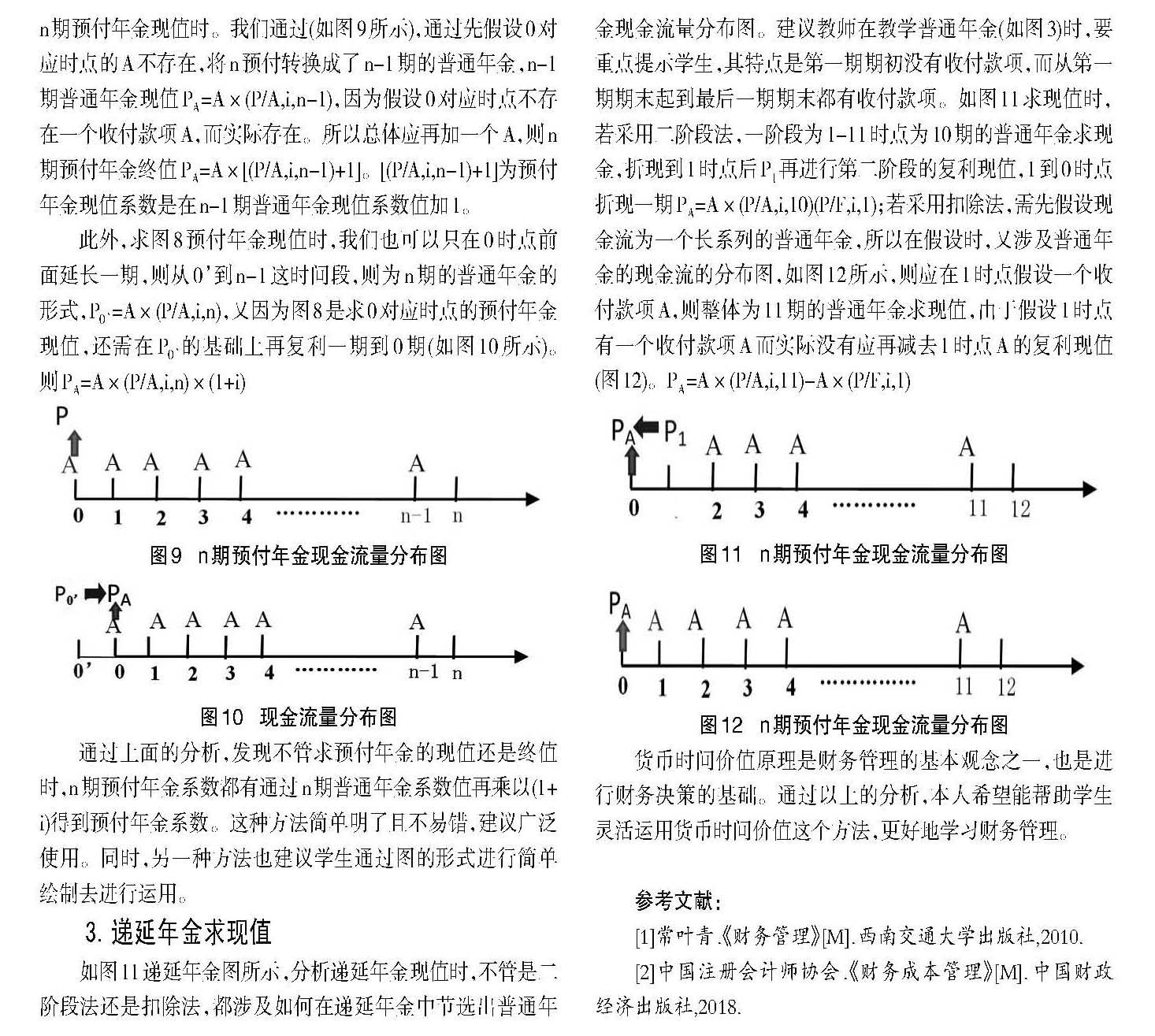
当涉及如图8所示的n期预付年金求现值时，如求图8的n期预付年金现值时。我们通过（如图9所示），通过先假设0对应时点的A不存在，将n预付转换成了n-1期的普通年金，n-1期普通年金现值PA=A×（P/A，i，n-1），因为假设0对应时点不存在一个收付款项A，而实际存在。所以总体应再加一个A，则n期预付年金终值PA=A×[（P/A，i，n-1）+1]。[（P/A，i，n-1）+1]为预付年金现值系数是在n-1期普通年金现值系数值加1。

此外，求图8预付年金现值时，我们也可以只在0时点前面延长一期，则从0到n-1这时间段，则为n期的普通年金的形式，P0=A×（P/A，i，n），又因为图8是求0对应时点的预付年金现值，还需在P0的基础上再复利一期到0期（如图10所示）。则PA=A×（P/A，i，n）×（1+i）

通过上面的分析，发现不管求预付年金的现值还是终值时，n期预付年金系数都有通过n期普通年金系数值再乘以（1+i）得到预付年金系数。这种方法简单明了且不易错，建议广泛使用。同时，另一种方法也建议学生通过图的形式进行简单绘制去进行运用。

3.递延年金求现值

如图11递延年金图所示，分析递延年金现值时，不管是二阶段法还是扣除法，都涉及如何在递延年金中节选出普通年金现金流量分布图。建议教师在教学普通年金（如图3）时，要重点提示学生，其特点是第一期期初没有收付款项，而从第一期期末起到最后一期期末都有收付款项。如图11求现值时，若采用二阶段法，一阶段为1-11时点为10期的普通年金求现金，折现到1时点后P1再进行第二阶段的复利现值，1到0时点折现一期PA=A×（P/A，i，10）（P/F，i，1）;若采用扣除法，需先假设现金流为一个长系列的普通年金，所以在假设时，又涉及普通年金的现金流的分布图，如图12所示，则应在1时点假设一个收付款项A，则整体为11期的普通年金求现值，由于假设1时点有一个收付款项A而实际没有应再减去1时点A的复利现值（图12）。PA=A×（P/A，i，11）-A×（P/F，i，1）

货币时间价值原理是财务管理的基本观念之一，也是进行财务决策的基础。通过以上的分析，本人希望能帮助学生灵活运用货币时间价值这个方法，更好地学习财务管理。

参考文献：

[1]常叶青.《财务管理》[M].西南交通大学出版社，2010.

[2]中国注册会计师协会.《财务成本管理》[M].中国财政经济出版社，2018.