巧构图 妙解题

田晓东

(黑龙江省哈尔滨市第二十四中学 150060)

求解某些数学问题，如果能挖掘题目中隐含的几何意义，构造出相应的几何图形，可将隐蔽的条件直观化，从而简化思维，获得直观、简捷、巧妙的解答.下面通过若干例子分类阐述.

一、构造数轴

例1 解不等式|x+2|+|x-2|<8.

解我们把数a在数轴上对应的点记为(a)，那么不等式左边表示点(x)到点(-2)、点(2)的距离之和.如图1所示，显然点(x)位于点(-4)与点(4)之间时，可使距离之和小于8.

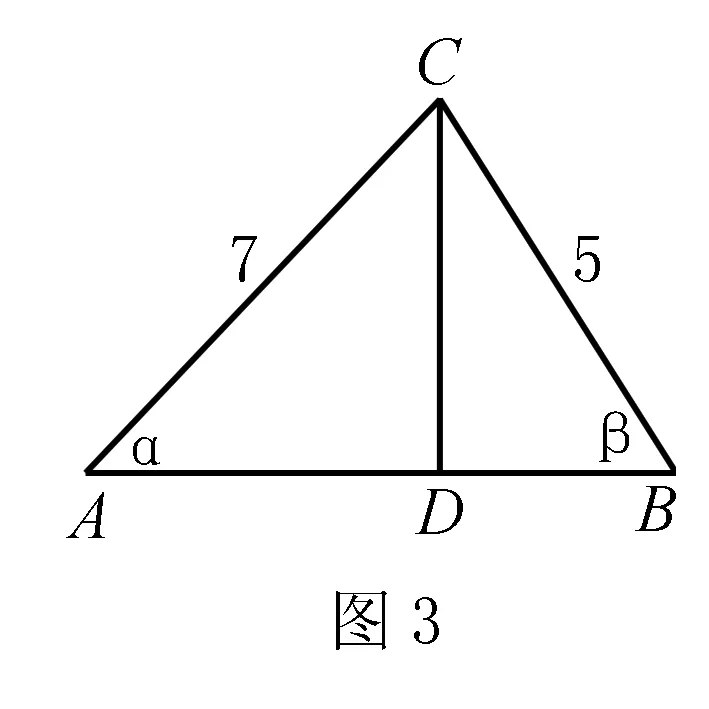
故不等式的解集为{x|-4

点评本题常规解法是分段讨论去掉绝对值，或用平方法去掉绝对值，但运算量都十分巨大，或将问题复杂化.而巧用绝对值的几何意义，画出数轴，答案直观，简捷获解.

二、构造图象

例2 (第15届全俄数学竞赛题)设x,y,z∈(0,1)，求证x(1-y)+y(1-z)+z(1-x)<1.

分析化多元为一元，构造出相应的函数，考查函数图象的位置.

证明以x为主元，y、z为参数，将不等式整理成关于x的函数式，即f(x)=(1-y-z)x+y+z-yz-1<0.

由条件x∈(0,1)，知函数f(x)的图象是定义在区间(0，1)上的一条线段.又由y、z∈(0,1)，知1-y>0,1-z>0,这样有

f(0)=y+z-yz-1=-(1-y)(1-z)<0,

f(1)=1-y-z+y+z-yz-1=-yz<0.

因此线段位于x轴下方，故有f(x)<0，从而得

x(1-y)+y(1-z)+z(1-x)<1.

三、构造三角形

例3 已知锐角α、β满足条件：7sinα=5sinβ,7cosα+5cosβ=7,求α+2β的值.

解由已知式可构造出如图3的△ABC，其中CD⊥AB,AC=7,BC=5,∠A=α,∠B=β.可见7sinα=CD=5sinB,∠A=α,∠B=β.可见7sinα=CD=5sinβ,AD=7cosα,BD=5cosβ,AB=AD+BD=7cosα+5cosβ=7=AC,故∠ACB=∠B=β.

所以α+2β=α+β+β=∠A+∠B+∠ACB=180°.

点评本题的常规解法是由已知式联立方程组，分别出求sinα、cosα、sinβ、cosβ,再利用和角及倍角公式计算sin(α+2β)或cos(α+2β),虽然方法可行，但运算量极大，且易错.而本文解法，由式子的结构特征构造出共直角边的两个角三角形，用各条边来表示各式，方法直观而简单.

四、构造圆

例4 (1986年高考题)在平面直角坐标系中，在y轴的正半轴上给定两点A、B，试在x轴的正半轴上求点C，使∠ACB取得最大值.

解不妨记A(0，a),B(0,b)(a>b>0),如图4.现过点A、点B作一圆，与x轴正半轴相切于点C，则点C即为所求.理由如下：

假设点D是x轴正半轴上异于点C的任一点，连结AC、BC、AD、BD，记AD与圆交于点E.由平面几何知∠D<∠AEB=∠ACB,因此点C使∠ACB最大.

点评本题的常规解法有三角法，解析几何法，复数法，再结合判别式，基本不等式来解答，过程繁难.而本解法构造出直线与圆相切，妙用切割线定理，几乎不算而解.

五、构造切线

例5 (2017年全国卷Ⅱ理21题)已知函数f(x)=ax2-ax-xlnx,且f(x)≥0恒成立，求a的值.

解注意到x>0，那么f(x)≥0恒成立等价于a(x-1)≥lnx对x∈(0,+∞)恒成立.

令h(x)=a(x-1),g(x)=lnx.易知h(x)的图象是过定点A(1，0)的直线系.而点A(1，0)也恰好在函数g(x)的图象上，那么由h(x)≥g(x)恒成立，知点A(1，0)应是两者图象的切点，因此直线斜率a应是曲线g(x)在点A(1，0)处的导数值.

点评本题无论是用最值法还是分离参数法，解法都很烦琐.而挖掘出式子的几何背景，由不等式a(x-1)≥lnx恒成立，转化为曲线的切线，使隐蔽问题直观化，稍算即解.

当然了，构造图形的方法多种多样，要由题目的不同而选用相应的图形.解题的关键是能够从题目的式子和问题中挖掘出图形，这要求具有敏锐的观察能力，丰富的想象能力，而这需要在平时的解题实践中注意积累和总结升华.